Занятие по рабочей программе №07
Дисциплина: БД.08 «Информатика»
Раздел 1. Информация и информационная деятельность человека.
Тема: Теория множеств и математической логики.
Цель занятия: Дидактическая:
сформулировать представление студентов о множестве и математической логике;
выяснить основные операции над множествами;
определение исчисление высказываний;
систематизировать и обобщить знания по применению теории множеств и алгебры логики;
углубить и закрепить знания по дисциплине «Информатика».
Воспитательная:
развивать коммуникативные способности;
развивать аналитические способности;
развивать творческий подход к процессу обучения.
воспитывать самостоятельность, дисциплинированность;
стимулировать студентов к изучению дисциплины;
побуждать к формированию активной жизненной позиции;
прививать уважение и любовь к будущей профессии.
Вид занятия: лекция.
Тип занятия: обобщение и систематизация знаний.
Форма проведения занятия: репродуктивная и эвристическая беседа.
Междисциплинарные связи:
Обеспечивающие Математика, Охрана труда, Безопасность жизнедеятельности.
Обеспечиваемые
Информационные технологии в профессиональной деятельности, и др.
Методическое обеспечение: опорный конспект.
Литература:
Симонович, С. В. Информатика. Базовый курс : Учебник для вузов. 3 - е изд. Стандарт третьего поколения. – СПб., 2016., стр.
В.А. Башкин, Л.Ю. Белова, Ю.А. Белов Элементы теории множеств и математи- ческой логики. Теория и задачи Учеб. пособие / Яросл. гос. ун-т. Ярославль : ЯрГУ, 2005. 79 с.
ХОД ЗАНЯТИЯ
Ознакомление с темой, целью и планом занятия.
Тема: Теория множеств и математической логики.
ПЛАН
Представления о множествах.
Операции над множествами.
Введение в математическую логику.
Исчисление высказываний
Значения формул. Таблицы истинности.
Применение теории множеств и алгебры логики.
Изложение и изучение нового материала.
ЛИТЕРАТУРА: [2], стр.
Представления о множествах
Теория множеств и алгебра логики являются основополагающими разделами математики и формальной логики. Эти разделы имеют широкое применение во многих областях науки и инженерии, таких как компьютерная наука, физика, экономика и другие. В этой главе мы рассмотрим основные понятия, принципы и методы теории множеств и алгебры логики.
Множества
Одно из основных понятий в теории множеств - это множество. Множество - это совокупность элементов, собранных вместе на основе некоторого общего свойства. Обозначение множества - фигурные скобки, внутри которых перечисляются его элементы.
Например, множество натуральных чисел от 1 до 5 может быть записано как {1, 2, 3, 4, 5}. Элементы множества не повторяются, и порядок элементов в множестве не имеет значения.
В теории множеств используются различные операции, такие как объединение, пересечение и разность множеств. Операция объединения множеств позволяет объединить все элементы двух или более множеств. Операция пересечения находит общие элементы двух или более множеств. Операция разности выполняет вычитание элементов одного множества из другого.
Понятие множества является базовым в математике, на его основе формируются другие понятия. В силу своей общности - это неопределяемое понятие.
Под множеством принято понимать любое собрание (совокупность) определенных и различимых между собой объектов, мыслимое как единое целое. Эти объекты называются элементами данного множества.
В приведенном выше описании понятия множества, которое принадлежит основателю теории множеств немецкому математику Г. Кантору, существенным является то, что собрание объектов (множество) само рассматривается как один предмет, как нечто целое. Относительно предметов, которые могут входить во множество, допускается значительная свобода. Важно, что наша интуиция должна, во-первых, отделять их один от другого даже тогда, когда их нельзя точно указать (например, множество простых чисел), во-вторых, давать ответ на вопрос о принадлежности объекта данному множеству. Последнее тесно связано со способами задания множеств.
Тот факт, что объект а является элементом множества А, другими словами а принадлежит множеству (содержится в множестве) А, символически обозначается а А. В противном случае пишут а А.
Г. Кантор сформулировал несколько интуитивных принципов, которые естественно считать выполняющимися для произвольных множеств. В частности интуитивный принцип объемности, который оговаривает условия равенства (тождественности) объектов нашей теории, а, следовательно, и их различия.
Интуитивный принцип объемности. Множества А и В считаются равными, если они состоят из одних и тех же элементов.
Записывают А = В , если А и В равны, и А В - в противном случае.
Пример. Пусть А - множество действительных корней уравнения х2 - 7х + 6 = 0 , а множество В состоит из чисел 1 и 6. Числа 1, 6 и только они являются корнями уравнения, следовательно, в силу принципа объемности заключаем, что А = В.
Множество А, элементами которого являются объекты а1, а2, ... , аn и только они, обозначают А = {а1, а2, ... , аn}.
Подмножества.
Если каждый элемент множества А являются одновременно и элементом множества В, то А называют подмножеством множества В, и пишут А В. В случае, когда А В, но А В, говорят , что А есть собственное подмножество В, и обозначают А В.
Ясно, что : 1) А А;
2) если А В, В С, то А С;
3) если А В, В А, то А = В.
Нужно различать отношения принадлежности ( ) и включения ( ). Если А = {а1, а2, ,... , аn}, то а1 А, но а1 А, т.к. а1 не является множеством, а значит и подмножеством А. Однако, если ввести в рассмотрение множество А1, состоящее из одного элемента а1 , А1 = {а1}, то А1 А или {а1} А.
Множество, не содержащее элементов, называется пустым множеством и обозначается .
Например, множество действительных корней уравнения х 2 + 1 = 0 является пустым множеством. Этот простой пример иллюстрирует целесообразность введения понятия пустого множества.
Пустое множество есть подмножество любого множества. Если определить множество С = {}, то оно содержит элемент - пустое множество.
Сами множества могут становиться элементами других множеств. Если А = { а1, а2 }, В = { b1, b2 }, то D = { A, B } не содержит в качестве элементов а1 или b1 , т.е. а1 D , но А D.
Для множества {a, b} рассмотрим все его подмножества: {a}, {b}, {a, b} и . Тогда множество {, {a}, {b}, {a, b}} представляет из себя - “множество всех подмножеств“ исходного множества {a, b}. Аналогично, для любого множества А можно определить множество всех его подмножеств S(A).
Множество, элементами которого являются все возможные элементы всех возможных множества, принято называть универсальным множеством (универсумом) и обозначать U. Таким образом, всякое множество является подмножеством универсального множества U.
Упражнения. Определите сколько элементов содержит множество S(A), если множество А содержит 0, 1, 2, 3, … , n элементов.
Способы задания множеств.
Множества могут задаваться различными способами. Можно просто перечислить все элементы множества, можно задать порождающую процедуру, т. е. указать правило, по которому из каких-то объектов строятся элементы множества, можно указать характеристическое свойство элементов данного множества, т. е. свойство, которым обладают элементы множества и только они и т. д. В связи с этим возникает проблема эффективного описания способов задания множеств. Ее решение обычно основано на интуитивном понятии “формы от х”. Под “формой от х” принято понимать конечную последовательность, состоящую из слов и символа х, такую, что если каждое вхождение символа х заменить одним и тем же именем некоторого предмета, то в результате получится истинное или ложное предложение. Например, формами от х будут предложения : “5 делит х”. “ х - родственник Иванова”. Напротив, предложения “для всех х х 2 - 4 = (х - 2)(х + +2)” или “существует такое х, что х 0” не являются формами от х.
Обозначим форму от х через Р(х), тогда можно сформулировать Интуитивный принцип абстракции. Любая форма Р(х) определяет некоторое множество А, а именно множество тех и только тех предметов а, для которых Р(а) - истинное предложение.
Запись А = { x| P(x) } означает, что множество А определяется формой Р(х).
Примеры: 1.{x| x - целое положительное число, меньшее 5} = {1,2,3,4}.
2. {x| x - буква русского алфавита, входящая в слово “мама”} = {а, м}.
3. {x| x = 2n, n - натуральное число} - множество четных натуральных чисел.
Операции над множествами
Рассмотрим операции над множествами, которые представляют собой ряд правил, позволяющих получать новые множества из заданных.
Объединением (суммой) двух множеств А и В называется множество А В, все элементы которого являются элементами множества А или В:
А В = {x | x A или x В}.
Другими словами, в объединение А В входят все элементы как множества А , так и множества В, т. е. А А В и В А В.
Пример 1. Если А = {1, 2, 3}, B = {0, 1, 5}, то А В = {0, 1, 2, 3, 5}.
Для любой совокупности множеств под их объединением будем понимать новое множество, каждый элемент которого является элементом некоторого множества из данной совокупности, при этом, любой элемент каждого множества совокупности есть элемент объединения. В частности, для А1, А2, ..., Аn, ..., A = A i = {x | x A i , i = 1,2, ..., n, ...}.
Пересечением множеств А и В называется множество А В, элементами которого являются элементы обоих множеств А и В:
А В = {x | x A и х В}.
Другими словами в пересечение А В входят только те элементы А, которые входят в В. Если ни один элемент множества А не является элементом множества В, то очевидно, что А В = . В этом случае говорят , что множества А и В не пересекаются. Ясно, что А В А и А В В.
Пример 2. Если А = {a, b, c, d}, B = {a, c, d, e, f}, то А В = {a, c, d}.
Для произвольной совокупности множеств под пересечением будем понимать новое множество, состоящее из тех и только тех элементов, которые входят во все множества данной совокупности. В частности, для А1, А2, ..., А n, ... , A = A i = {x | x A i , для всех i = 1,2, ..., n, ...}.
Разностью множеств А и В называется множество А \ В, элементами которого являются только те элементы множества А, которые не принадлежат множеству В:
А \ В = {x | x A , но х В}.
Например, для множеств А и В из примера 2 А \ В = {b}.
Симметрической разностью множеств А и В называется множество А В = (А \ B) (B \ A). Другими словами, это множество состоит из тех и только тех элементов А и В, которые не входят в пересечение этих множеств.
Например, для множеств А и В из примера 2 А В = {b, e, f}.
Можно доказать, что А В = (А \ B) (B \ A) = (А B) \ (А В).
Дополнением множества А называется множество А всех тех элементов, которые не принадлежат А.
всех тех элементов, которые не принадлежат А.
Если предположить существование универсума U, то А = U \ A.
Если А Х то разность Х \ А = {x | x X, x A}, т.е. множество всех элементов Х, которые не принадлежат А, иногда называют относительным дополнением множества А до множества Х. Отметим, что Х \ A = X А.
Для наглядного представления отношений между подмножествами какого-либо универсального множества используют диаграммы Эйлера - Венна. Само универсальное множество U изображают в виде прямоугольника, а его подмножества - в виде кругов, расположенных внутри прямоугольника.
Диаграммы Эйлера - Венна, иллюстрирующие операции над множествами:
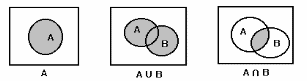
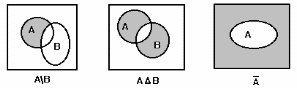
Рис. 1
Для любых подмножеств А, В и С универсального множества U выполняются следующие тождества:
1. Коммутативность:
А В = В А ; А В = В А ;
2. Ассоциативность:
А (В С) = (А В) С; А (В С) = (А В) С;
3. Дистрибутивность:
А (В С) = (А В) (А С); А (В С) = (А В) (А С);
А = А, А U = U; А = , А U = А;
А А = U ; А А = ;
4. Идемпотентность:
А А = А; А А = А;
5. Законы де Моргана:
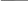
 А В = А В; А В = А В;
А В = А В; А В = А В;
6. Закон поглощения:
А (А В) = А; А (А В) = А.
Введение в математическую логику
Алгебра логики
Алгебра логики является математической структурой, используемой для изучения и моделирования логических выражений и операций. Она основана на идеях булевой алгебры и содержит набор операций, таких как конъюнкция, дизъюнкция и отрицание.
Конъюнкция (логическое "и") представляет собой операцию, которая дает истинное значение только в том случае, если оба участвующих выражения истинны. Дизъюнкция (логическое "или") дает истинное значение, если хотя бы одно из выражений истинно. Отрицание меняет истинность выражения на противоположную.
Алгебра логики предоставляет набор правил и законов, таких как законы де Моргана и закон двойного отрицания, которые позволяют моделировать и преобразовывать логические выражения. Это позволяет упрощать сложные логические выражения и делать выводы на основе заданных условий.
Согласно одному из самых распространенных определений, логика есть анализ методов рассуждений. Изучая эти методы, логика интересуется в первую очередь формой, а не содержанием доводов в том или ином рассуждении. Логику не интересует истинность или ложность отдельных посылок или заключений, она лишь желает знать, вытекает ли истинность заключения из истинности посылок. Одна из основных задач логики – систематическая формализация и каталогизация правильных способов рассуждений.
Математическая логика, как любая другая математическая дисциплина предметом своего изучения имеет математическую модель, в данном случае - модель человеческих рассуждений и правил умозаключений. И как всякая модель она и адекватна, и не совпадает с самой содержательной логикой.
Исчисление высказываний
Элементарные высказывания. Логические связки. Формулы. В содержательной логике под высказыванием понимается законченная мысль. Это может быть некоторое предложение, о котором имеет смысл говорить истинно оно или ложно, или несколько предложений, связанных между собой определенным образом. Таким образом, можно выделить элементарные высказывания (первокирпичики) и более сложные высказывания, которые по определенным правилам строятся из элементарных.
В математической логике элементарные высказывания моделируются элементами некоторого произвольного множества.
Пусть М - некоторое множество, его элементы будем называть элементарными высказываниями, и обозначать, как это принято в математической логике, большими латинскими буквами (иногда с индексами). Само множество М = {A, B, C, ... , A 1, ... , A i, ...} будем называть множеством элементарных высказываний. При анализе способов построения сложных высказываний в разговорной речи можно выделить основные связки: “не”, “и”, “или”, “если ..., то...”, “тогда и только тогда” и др. В математической модели им соответствует другое множество, элементы которого называются логическими (пропозициональными) связками. Множество логических связок включает в себя следующие связки : - отрицание (читается: “не”), & () - конъюнкция (“и“), - дизъюнкция (“или”), - импликация (“если..., то ...”), - эквивалентность (“тогда и только тогда”). Кроме того, в математической логике используются и другие связки, в частности, - квантор всеобщности (“каждый”, “любой”, “всякий”), - квантор существования (“существует”, “найдется”). Множество элементарных высказываний и множество логических связок никогда не пересекаются.
Теперь мы должны формализовать правила построения сложных высказываний из элементарных. Из множества элементарных высказываний М с помощью множества логических связок построим новое множество Ф, которое будем называть множеством формул. Правило построения множества Ф состоит из 3-х условий ( такой способ определения называют индуктивным).
Определение 1. Множество Ф является множеством формул, если выполняются следующие условия:
1) всякое элементарное высказывание есть формула, (М Ф);
2) если F1 и F2 - формулы (F1 , F2 Ф), то ( F1), (F1 & F2), (F1 F2), (F1 - F2), (F1 F2) - формулы;
3) других формул нет.
В качестве примера выясним, является ли высказывание А(В) формулой ? Это не элементарное высказывание (в его записи присутствуют логические связки), следовательно, по условию 1) оно не может быть формулой. Так как А и В - элементарные высказывания, то по условию 1) это формулы, тогда (В) - формула по условию 2). Но само выражение А (В) формулой не является, так как не заключено в скобки (сравните с условием 2), а условие 3) утверждает, что других формул нет. Таким образом, по формальным основаниям указанное выражение формулой не является.
Значения формул. Таблицы истинности
Рассмотрим высказывания с точки зрения их истинностных значений. В содержательной логике под высказыванием подразумевается повествовательное предложение, о котором можно определенно сказать истинно оно или ложно. Например, предложение “ квадрат является ромбом” - высказывание, причем истинное, а предложение “рассмотрим множество всех функций” высказыванием не является, так как нельзя с определенностью утверждать, истинно оно или ложно. Таким образом, в нашей математической модели каждое элементарное высказывание нужно рассматривать как переменную величину (пропозиционную переменную), которая принимает только два значения “истина” и “ложь”. Значение “истина” принято обозначать через единицу - 1, а “ложь” через ноль - 0. Итак, всякое элементарное высказывание (пропозиционная переменная) формально может принимать одно из значений: 1или 0.
Формулы логики высказываний, которые мы определили, выше являются высказываниями, следовательно, тоже должны принимать одно из истинностных значений. Для формул, которые являются таковыми по условию 1), мы уже приняли соглашения (элементарные высказывания). Чтобы определить истинностное значение любой формулы из условия 2), нужно, прежде всего, определить значения формул: А, (А & В), (А В), (А В), (А В) в зависимости от значений входящих в них элементарных высказываний. Это делается с помощью, так называемой таблицы истинности.
| А | В | А | (А & В) | (А В) | (А В) | (А В) |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
Логические связки отрицание, конъюнкцию, дизъюнкцию, импликацию, эквивалентность можно рассматривать как функции, которые определены на двуэлементном множестве {0, 1} со значениями в этом же множестве. Их называют логическими (булевыми) функциями или операциями. Операция отрицания - унарная, а все остальные - бинарные. Таблицу истинности для каждой из операций можно рассматривать как определение этой операции.
Из определения формулы следует, что с помощью таблицы истинности можно определить истинностные значения любой формулы. Рассмотрим это на примере.
Пример 1. Найти истинностные значения формулы
F = ((A B) (( A) & B)).
Убедимся, что F формула. Так как А и В - формулы, то (A), (A B) - формулы по условию 2). Тогда в силу этого же условия формулами являются ((A) & B) и F = ((A B) (( A) & B)). Рассмотренные нами выше составные части формулы F, которые сами являются формулами, называются подформулами формулы F.
Для нахождения всех истинностных значений формулы F последовательно найдем значения подформул. Представимы эти вычисления в виде общей таблицы истинности.
| А | В | (А) | (А В) | ((А) & В) | ((А В) ((А) & В)) |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
Тавтологии. Среди всех логических формул особый интерес представляют такие, которые истинны уже в силу одной только своей функционально- истинностной структуры. Такую формулу можно рассматривать как модель логического закона.
Определение 2. Формула А называется тавтологией (тождественно- истинной формулой), если при любых значениях пропозициональных переменных она принимает значение “истина” (1).
С помощью таблицы истинности тавтологию можно определить как формулу, для которой соответствующий ей в таблице столбец целиком состоит из 1. Таким образом, построение таблицы истинности это эффективная процедура для решения вопроса о том, является ли данная формула тавтологией.
Из таблицы истинности для импликации очевидно следует, что при любых значениях пропозиционной переменной А формула (А А) принимает значение 1, т.е. является тавтологией.
Из определения конъюнкции легко получаем, что формула (&()) всегда принимает значение 0 (“ложь”). Тогда формула ((&())) принимает только одно значение -1 (“истина”), т.е. является тавтологией.
В данном примере мы встретились с формулой ( & ()), которая всегда принимает значение Л. Такие формулы называют противоречиями (тождественно-ложными формулами). Очевидно, что формула А является тавтологией тогда и только тогда, когда формула () - противоречие.
Докажем несколько утверждений общего характера о тавтологиях.
1. Если А, (А В) - тавтологии, то тавтологией является В.
Предположим , что В не является тавтологией. Тогда В принимает значение “ложь” при некотором наборе значений пропозиционных переменных. Но при этом же наборе значений переменных А имеет значение “истина”, так как А - тавтология (по условию). В таблице истинности такому набору значений А и В импликации (А В) соответствует значение “ложь”. Получили противоречие с условием, что (А В) - тавтология.
2. Если А - тавтология, содержащая пропозиционные переменные А1, А2 , ... , Аn , и В получается из А подстановкой формул Ф1, Ф2 , ... , Фn вместо А1, А2 , ... , Аn соответственно, то В есть тавтология, т.е. подстановка в тавтологию есть тавтология.
Доказательство: Обозначим А = А (А1, А2 , ... , Аn ), тогда В символически запишется В = А (Ф1, Ф2 , ... , Фn ). Нам нужно показать, что 1) В - формула; 2) В - тавтология. Первое следует из определения формулы и из того, что Ф1, Ф2 , ... , Фn - формулы. Пусть задан некоторый набор значений для пропозиционных переменных формулы В. Формулы Ф1, Ф2 , ... , Фn примут тогда некоторые значения х1, х2 , ... , хn (каждое хk есть И или Л). Если мы придадим значения х1, х2 , ... , хn соответственно пропозиционным переменным А1, А2 , ... , Аn, то значение А совпадет с истинностным значением В при заданном распределении значений пропозиционных переменных, входящих в В. Так как А по условию тавтология, то В при этом наборе значений переменных примет значение “истина”. Таким образом, В всегда принимает значение И, т.е. является тавтологией.
Пример 2. Формула F=(A(BA)) является тавтологией. Действительно, если предположить, что F принимает значение Л, то А - И, а ( В А) - Л. Но импликация (В А) принимает значение Л только в том случае, когда В - И , а. А - Л. Получили противоречие с тем, что А - И. Рассмотрим формулы Ф1 = С& A и Ф2 = ((С) А). Заменим в формуле F пропозиционную переменную А на Ф1 , а В на Ф2 , соответственно. Получим новую формулу F*= ((С& A) (((С) А) (С& A))), которая является тавтологией. Убедимся в этом, составив для нее таблицу истинности.
| А | С | ( С) | (( C) A) | (С & A) | ((( C) A)(C& A)) | F* |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
Если в формуле F заменить только А на Ф1 , то получим еще одну тавтологию F** = = ((С& A) (B (С& A))).
| А | В | С | (С& A) | (B (С& A)) | ((С& A) (B (С& A))). |
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Полные системы связок. В этом разделе мы рассмотрим множество логических связок с точки зрения взаимозаменяемости его элементов. Наша задача, выбрать такое минимальное подмножество, с помощью которого можно будет определить все остальные логические связки. Такое подмножество называется полным.
Определение 3. Две формулы F и Ф (F = Ф) называются логически эквивалентными ( равносильными), если ( F Ф ) - тавтология.
Из определения следует, что F равносильна Ф тогда и только тогда, когда в таблице истинности соответствующие столбцы совпадают.
Покажем, что формула (А В) равносильна формуле ((А) В).
| А | В | А | (А В) | ((А) В) |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
Равносильность (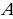 В) = ((А) В) показывает, что связку можно исключить, заменив ее связками и . Связку & можно исключить в силу равносильности (А & В) = ((А) (В)). Так как (А В) = ((А В) & (В А)), а связки и & можно выразить через отрицание и дизъюнкцию, то связка так же может быть исключена. Это показывает, что система связок { , } полна.
В) = ((А) В) показывает, что связку можно исключить, заменив ее связками и . Связку & можно исключить в силу равносильности (А & В) = ((А) (В)). Так как (А В) = ((А В) & (В А)), а связки и & можно выразить через отрицание и дизъюнкцию, то связка так же может быть исключена. Это показывает, что система связок { , } полна.
Применение теории множеств и алгебры логики
Теория множеств и алгебра логики имеют множество практических применений. В информатике, алгебра логики используется для разработки логических схем и систем, таких как компьютеры и цифровые схемы. Она позволяет строить и анализировать логические выражения и функции, основанные на принципах булевой алгебры.
В математике, теория множеств используется для формализации и структурирования математических объектов и отношений. Множества могут быть использованы для определения чисел, функций, отношений и других математических объектов. Они являются ключевыми понятиями во многих областях математики, включая анализ и алгебру.
Решение задач по теории множеств с помощью таблиц истинности. Если на выражения х А, у В посмотреть как на элементарные высказывания, то каждая формула теории множеств может быть заменена формулой логики высказываний. Это позволяет метод таблиц истинности применить к решению задач по теории множеств. Сведем этот способ решения задач к таблице.
| Формулы теории множеств | Формулы логики |
| А B А В А \ В А В = (А \ B) (B \ A) | А В А В ( A B) ( A B) ( B A) |
Например, докажем равенство (А В) = (А \ В ). Переведем это равенство в доказательство равносильности формул ((А) В) = (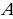 В), для чего воспользуемся таблицей истинности на предыдущей странице, показывающей их равносильность.
В), для чего воспользуемся таблицей истинности на предыдущей странице, показывающей их равносильность.
Упражнения:
Приведите два примера равных множеств.
Определите сколько элементов содержит множество S(A), если множество А содержит 0, 1, 2, 3, … , n элементов.
ДОМАШНЕЕ ЗАДАНИЕ
Составить конспект лекции.
Выполнить упражнения.
Пройти Тест входного контроля знаний, согласно своего Варианта.
Примечание. Вариант Теста распечатать, заполнить свои данные, ответить на вопросы теста и передать преподавателю.
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы.
Основные источники:
1. Симонович, С. В. Информатика. Базовый курс : Учебник для вузов. 3 - е изд. Стандарт третьего поколения. – СПб., 2016
2. Гохберг, Г.С. Информационные технологии : учебник для студ. сред. проф. Образования / Гохберг, Г.С, Зафиевский, А.В., Короткин, А.А.- 5-е изд., стер. – М. : Издательский центр «Академия», 2010. – 208с.
3. Филимонова, Е.В. Информационные технологии в профессиональной деятельности : учебник. – Изд-е 2-е, доп. и перераб. – Ростов н/Д : Феникс, 2008. – 381. – (СПО).
4. Е.В. Михеева, О.И. Титова Информатика Учебник 6-е издание М., Издательский центр «Академия», 2011 г
Дополнительные источники:
Колесниченко, О.В., Шишигин, И.В. Аппаратные средства PC. 5-е издание. СПб. БХВ - Петербург, 2006.
Ральф Вебер. Сборка, конфигурирование, настройка, модернизация и разгон ПК. - ДиаСофт, 2007.
Гребенюк, Е.И., Гребенюк, Н.А. Технические средства информатизации: учебник для студ. учреждений сред. проф. образования / Е. И. Гребенюк, Н.А.Гребенюк. – 9-е изд., перераб. и доп. – М. : Издательский центр «Академия», 2014. – 352 с.
Максимов, Н. В., Партыка, Т. JI., Попов, И. И. Технические средства информатизации : учебник / Н. В. Максимов, Т. JI. Партыка, И. И. Попов. — 3-е изд., перераб. и доп. — М. : ФОРУМ, 2010. — 608 с.
Гук, М. Аппаратные средства IBM PC. Энциклопедия. – СПб. : Питер, 2003. – 928 с.
Технические средства информатизации. Учебное пособие. / Составитель А.Н. Попов. – Нижневартовск : НГСГК, - 2007. – 331 с.
Интернет - источники:
Электронный учебник по информатике и информационным технологиям - http://www.ctc.msiu.ru/
Тесты по информатике - http://www.ege.ru/







 всех тех элементов, которые не принадлежат А.
всех тех элементов, которые не принадлежат А.

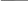
 А В = А В; А В = А В;
А В = А В; А В = А В;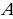 В) = ((А) В) показывает, что связку можно исключить, заменив ее связками и . Связку & можно исключить в силу равносильности (А & В) = ((А) (В)). Так как (А В) = ((А В) & (В А)), а связки и & можно выразить через отрицание и дизъюнкцию, то связка так же может быть исключена. Это показывает, что система связок { , } полна.
В) = ((А) В) показывает, что связку можно исключить, заменив ее связками и . Связку & можно исключить в силу равносильности (А & В) = ((А) (В)). Так как (А В) = ((А В) & (В А)), а связки и & можно выразить через отрицание и дизъюнкцию, то связка так же может быть исключена. Это показывает, что система связок { , } полна.









