Тригонометрия в окружающем мире и жизни человека

Муниципальное бюджетное общеобразовательное учреждение

Суховская средняя общеобразовательная школа

ИНДИВИДУАЛЬНЫЙ ПРОЕКТ

Тема: Тригонометрия в окружающем мире

и жизни человека

Работу выполнила:

Ученица 11 класса

……………………….

Руководитель проекта:

Бильник Татьяна Николаевна

п. Новосуховый, 2024

СОДЕРЖАНИЕ

ВВЕДЕНИЕ ………………………………………………………… 3

1.История тригонометрии 3

1.1 Истоки тригонометрии 4

1.2 Возникновение тригонометрии как науки 4

2. Тригонометрия в алгебре 5

2.1 Тригонометрические тождества 5

3. Тригонометрия в физике 6

3.1 Преломление света 6

3.2 Колебания и волны 7

4. Тригонометрия в биологии 7

4.1 Биоритмы 7

4.2 Движение животных 8

5. Тригонометрия в медицине 9

5.1 Формула сердца 10

5.2 Ортопедия 10

5.3 Радиология 10

6. Тригонометрия в навигации 10

6.1 Навигация в водном пространстве и в небе 11

7. Тригонометрия в строительстве 11

7.1 Искусство и архитектура 12

ЗАКЛЮЧЕНИЕ 13

Список литературы 14

Введение

Нет ни одной области математики, которая когда-нибудь не окажется применимой к явлениям действительного мира. (Н.И. Лобачевский)

В настоящее время большое внимание уделяют математике, как одной из областей научной деятельности. Одной из составляющих математики является тригонометрия. Сложно представить, но с этой наукой мы сталкиваемся не только на уроках математики, но и в нашей повседневной жизни.

Тригонометрия - раздел математики, в котором изучаются тригонометрические функции и их практическое применение.

В моём проекте «тригонометрия в окружающем мире и жизни человека» мы рассмотрим практическое применение тригонометрических функций и их свойства.

Актуальность темы проекта заключена в том, что знания в сфере тригонометрии откроют новые, возможно более удобные способы решения задач в разных областях науки.

Цель: определить связь тригонометрических функций с явлениями окружающего мира и деятельностью человека, в жизни.

Задачи:

1. Познакомиться с историей возникновения и развития тригонометрии.

2. Рассмотреть примеры применения тригонометрических функций в окружающем мире.

3. Выяснить, какие законы природы выражаются тригонометрическими функциями

Объект  исследования – тригонометрические функции; 

Предмет исследования - области их практического применения

1.История тригонометрии

Тригонометрия (от др. – греч. «треугольник» и «измеряю», то есть измерение треугольников) раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии.

Этот термин появился в 1595 году. Его ввёл в употребление немецкий математик и богослов Варфоломей Питиск, автор учебника по тригонометрии и тригонометрических таблиц. Сама же наука ещё в глубокой древности использовалась для расчётов в различных сферах деятельности человека. Тригонометрические вычисления применяются практически во всех областях наук.

1.1Истоки тригонометрии

Рис.1 Гиппарх – греческий астроном

Р уководствуясь данными о сохранившихся научных реликвиях, исследователи сделали вывод, что история возникновения тригонометрии связана с работами греческого астронома Гиппарха (рис.1), который впервые задумался над поиском способов решения треугольников (сферических).

История тригонометрии началась более двух тысяч лет назад. Первоначально её возникновение было связано с необходимостью выяснения соотношений углов и сторон треугольника. Затем тригонометрия существовала как часть астрономии. Позже она стала использоваться в архитектуре. А со временем её учились применять в различных областях человеческой деятельности.

Рис.2 Птолемей

История развития тригонометрии в Древней Греции связана с именем астронома Птолемея (рис.2). Греческим астрономам не были известны синусы, косинусы и тангенсы. Они пользовались таблицами, позволяющими найти значение хорды окружности с помощью стягиваемой дуги. Единицами для измерения хорды были градусы, минуты и секунды.

Тригонометрия выросла из человеческой практики, в процессе решения конкретных практических задач в областях астрономии, мореплавания, в составлении географических карт и т.д.

1.2Возникновение тригонометрии как науки.

История возникновения тригонометрии как обособленного раздела математического учения началась в Средневековье. Именно тогда ученые заменили хорды синусами. Это открытие позволило ввести функции, касающиеся исследования сторон и углов прямоугольного треугольника. То есть именно тогда тригонометрия начала обосабливаться от астрономии, превращаясь в раздел математики. Первый специализированный трактат по т ригонометрии появился в X—XI веке. Автором его был среднеазиатский учёный Аль-Бируни (рис.3).

Рис.3 Аль-Бируни

По мнению исследователей, история тригонометрии в Европе связана с именем англичанина Ричарда Уоллингфордского, который стал автором сочинения «Четыре трактата о прямых и обращенных хордах». Именно его труд стал первой работой, которая целиком посвящена тригонометрии. Во второй половине XVI века эта тема заинтересовала многих выдающихся людей того времени, в том числе Николая Коперника, Иоганна Кеплера, Франсуа Виета. Коперник отвел тригонометрии несколько глав своего трактата «О вращении небесных сфер» (1543). Чуть позже, в 60-х годах XVI века, Ретик - ученик Коперника - приводит в своем труде «Оптическая часть астрономии» пятнадцатизначные тригонометрические таблицы. Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.

2.Тригонометрия в алгебре

Первое, и самое очевидное, место применения тригонометрии – это ее применение в алгебре. Именно благодаря тригонометрическим функциям решаются очень сложные, требующие больших вычислений уравнения и задачи.

2.1Тригонометрические тождества

Рис.4 Тригонометрический круг

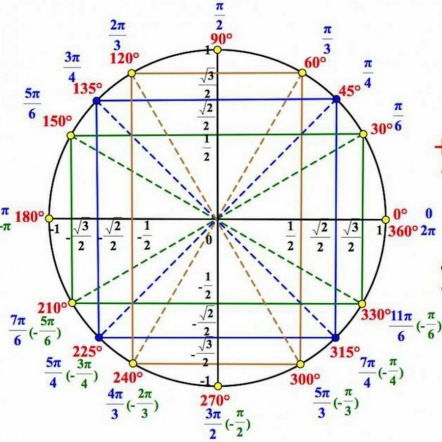
О сновные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности. Они позволяют выразить одну тригонометрическую функцию через любую другую. Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого «тригонометрического круга» (рис.4), то вся тригонометрия будет вам подвластна.

3.Тригонометрия в физике

В окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Механическими колебаниями называют движения тел, повторяющиеся точно или приблизительно через одинаковые промежутки времени. Примерами простых колебательных систем могут служить груз на пружине или маятник. Колебания маятника приближенно происходят по синусоидальному закону. Чем длиннее маятник, тем медленнее он качается.

3.1 Преломление света

Теория радуги.

Впервые эта теория была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях. (рис.5)

Рис.5 Преломление света в капле воды

Рис.6 Отражение лучей света в капле

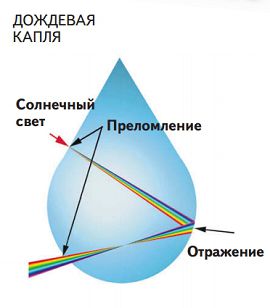
Р адуга возникает из-за того, что солнечный свет испытывает преломление в капельках воды, взвешенных в воздухе по закону преломления. Когда световой луч проходит границу между менее плотной оптической средой, например воздухом, и более плотной оптической средой, например водой, часть светового луча не проникает внутрь новой среды, а отражается от её поверхности (рис.6). Другая же часть светового луча проникает внутрь, но, уже меняя направление. Это явление называется преломлением света, и ученые уже давно могут не просто наблюдать, но и точно рассчитывать угол этого преломления. Оказалось, что простейшие тригонометрические формулы и знание синуса угла падения и угла преломления дают возможность узнать постоянный коэффициент преломления для перехода светового луча из одной конкретной среды в другую.

3.2 Колебания и волны

Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f(t). Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту или по струне. Если смещение частиц происходит в направлении распространения волны, такая волна называется продольной. Волны в упругом стержне или звуковые волны в газе являются примерами таких волн. Волны на поверхности жидкости имеют как поперечные, так и продольные компоненты. Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

Рис.7 Груз на пружине и на маятнике

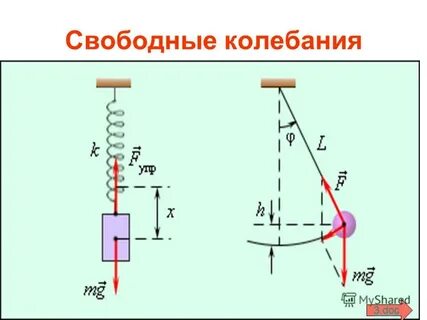
П римерами простых колебательных систем могут служить груз на пружине или математический маятник (рис.7). Графическое изображение этой функции, дающее наглядное представление о протекании колебательного процесса во времени удобно рассмотреть с помощью модели маятника программы « Функции и графики».

4.Тригонометрия в биологии

Изучив роль тригонометрии в физике, можно сделать вывод о том, что она отлично подходит для описания цикличных, периодичных процессов. В таких разделах науки как биология тригонометрия используется для тех же целей. То есть для исследования и описания биологических цикличных процессов.

4.1Биоритмы

Рис.8 Биоритмы

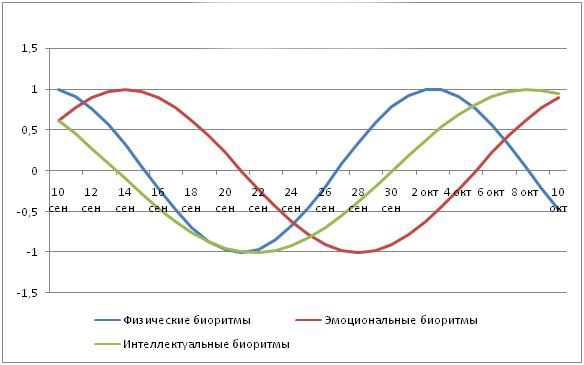
Биологические ритмы (биоритмы) — периодически повторяющиеся изменения характера и интенсивности биологических процессов и явлений. Являются фундаментальным процессом в живой природе. Биоритм представляет собой последовательность повторяющихся циклов (рис.8). Цикл, в свою очередь, это завершённое колебание, отклонение определённого показателя от исходной величины с возвратом к ней через н екоторое время. Выделяют следующие характеристики биоритмов: фаза, период, частота и амплитуда. Все живые существа на Земле подчиняются суточным биологическим ритмам. Например, у человека в зависимости от времени суток циклически меняются физиологическое и эмоциональное состояние. Существует способ вычисления биоритмов человека по трем фазам (физической, интеллектуальной и эмоциональной) и по дате рождения, однако большинство ученых считают его псевдонаучным и относят к всевозможным способам «предсказания» будущего.

Физический биоритм – регулирует физическую активность. В течение первой половины физического цикла человек энергичен, и достигает лучших результатов в своей деятельности (вторая половина – энергичность уступает лености).

Эмоциональный ритм – в периоды его активности повышается чувствительность, улучшается настроение. Человек становится возбудимым к различным внешним катаклизмам. Если у него хорошее настроение, он строит воздушные замки, мечтает влюбиться и влюбляется. При снижении эмоционального биоритма происходит упадок душевных сил, пропадает желание, радостное настроение.

Интеллектуальный биоритм - он распоряжается памятью, способностью к обучению, логическому мышлению. В фазе активности наблюдается подъем, а во второй фазе спад творческой активности, отсутствуют удача и успех.

В действительности человек зависит от биоритмов (например, мозговая и физическая деятельность и её результаты напрямую зависят от времени суток).

Однако определение будущего эмоционального и физического состояния человека, основанное на дате рождения, не может являться достоверным, хоть и в его расчете используется построение графиков тригонометрической функции синуса.

4.2 Движение животных

Когда рыба перемещается в воде, то её тело совершает сложные колебания, благодаря которым рыба может развить очень большие скорости, недоступные современным надводным и подводным кораблям. Рыбы используют, по крайней мере, два способа плавания – волнообразно извиваясь всем телом или двигая в основном только хвостом. Рыбы, имеющие змееобразную форму (например, угорь), плавают первым способом, так что изгиб тела движется от головы к хвосту «отталкивая» назад воду, в результате чего рыба движется вперёд. При втором способе воду «отталкивает» назад только быстро распрямляющийся хвост рыбы. Но даже в самом простом случае туловище и хвост изгибаются в противофазе, образуя кривую подобную синусоиде (рис.9).

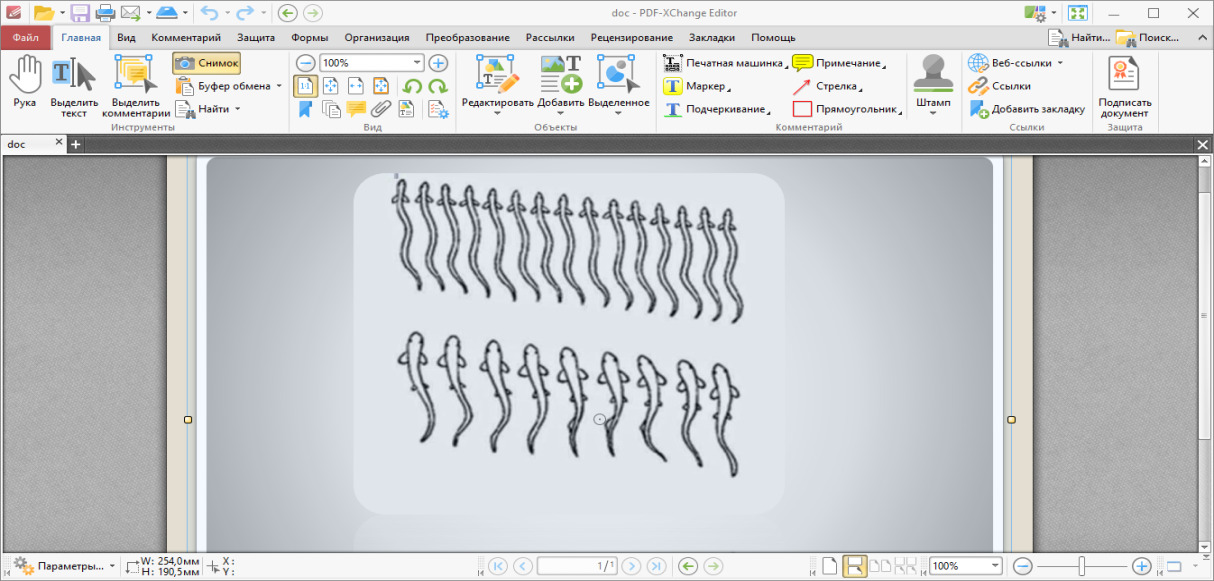
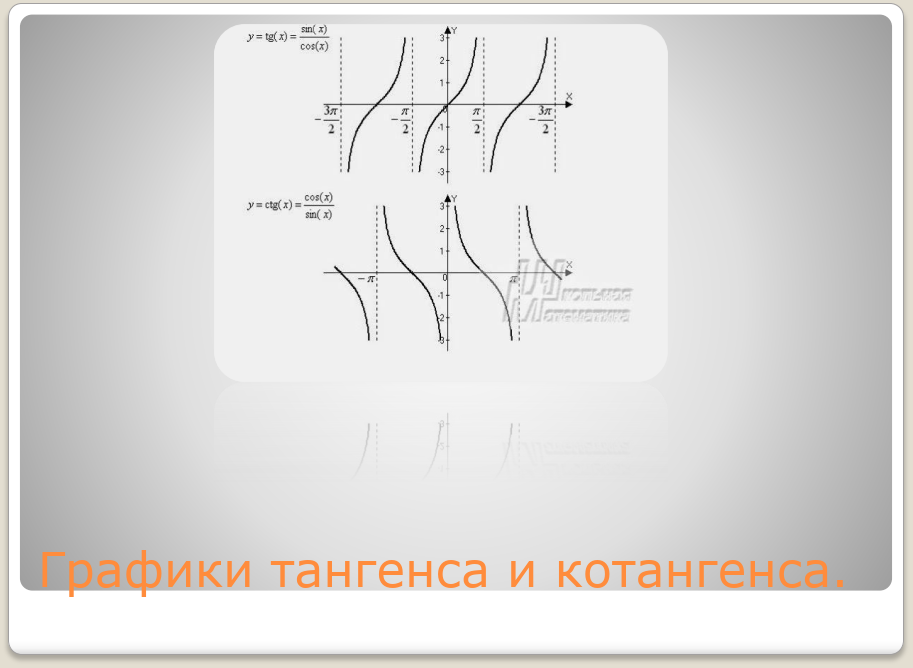
Рис.9 Движение рыб подобное синусоиде

5.Тригонометрия в медицине

Тригонометрия играет важную роль в таком разделе медицины как кардиология, ортопедия, радиология. Проблема математических описаний физиологических функций организма – вторая по значимости проблема после проблемы ДНК человека. В будущем будут вычислены формулы органов человека, и медики с помощью уравнений смогут прогнозировать и лечить любую болезнь

5.1Формула сердца

Рис.10 Графики ритма сердца

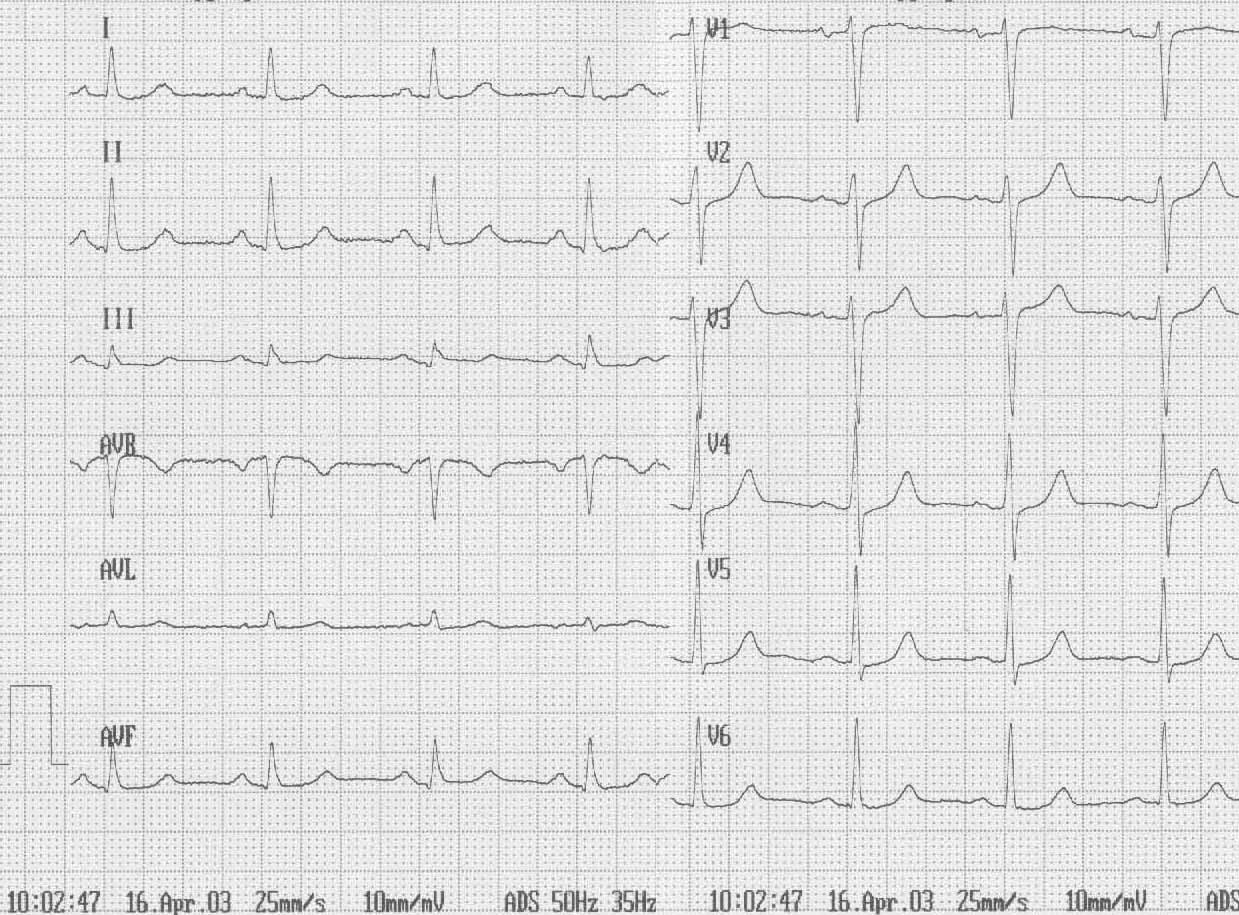
Н апример, иранские ученые нашли способ систематизировать информацию, связанную с электрической активностью сердца (рис.10). Сделать это им удалось выводом комплексного алгебраически-тригонометрического равенства, которое состоит из 8 выражений, 32 коэффициентов и 33 параметров, включающих в себя и дополнительные, необходимые для расчета в случаях аритмии. В средствах массовой информации и в среде ученых это равенство получило красноречивое название «формула сердца».

5.2Ортопедия

Рис.11 Отклонение позвонков в градусах

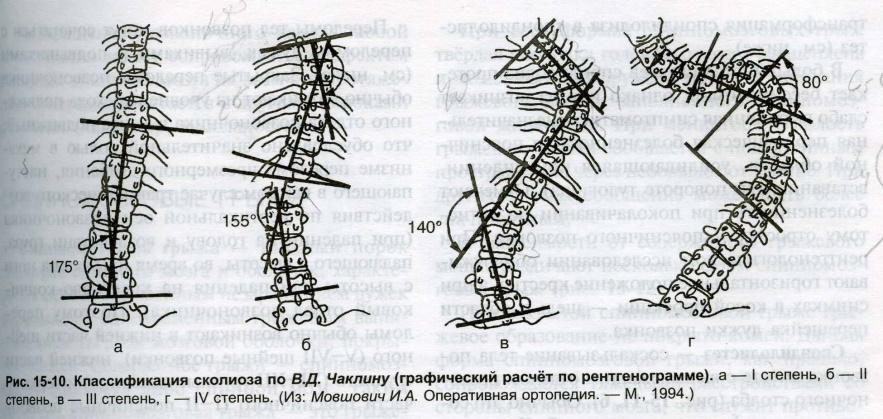
О ртопедия - раздел клинической медицины, раздел хирургии, изучающий профилактику, диагностику и лечение деформаций и нарушений функций костно-мышечной системы, которые являются результатом врождённых дефектов, пороков развития, последствий травм или заболеваний

Тригонометрия используется также в ортопедии, чтобы найти отклонение позвонка в градусах (рис.11) и узнать, повреждены ли нервы. Тригонометрические свойства также используются для формования протезов рук и ног, размеры которых для каждого человека нужно подбирать индивидуально.

5.3Радиология

Радиология - раздел медицины, изучающий применение лучевых методов для лечения различных заболеваний. Диагностическая радиология помогает специалистам в области здравоохранения видеть структуры тела человека. Радиолог использует ультразвук, ядерную медицину и магнитный резонанс для диагностики или устранения заболеваний. Здесь также используются свойства тригонометрии, чтобы получить правильные углы, что обеспечивает точное попадание луча в раковые клетки.

6.Тригонометрия в навигации

Тригонометрия в навигации является основой для расчёта расстояний, высот, местоположений, составления карт. Также навигация необходима: летчикам, которые управляют сложными высокотехничными самолетами, ориентируются, порой в очень экстремальных ситуациях, космонавтам, чья работа связана с риском для жизни, со сложным построением маршрута и его освоением.

6.1Навигация в водном пространстве и в небе

П ри плавании по Средиземному морю в лоциях (раздел судовождения, в котором изучаются условия плавания судов по водным путям) до XVII века широта не указывалась. Впервые применил тригонометрические расчёты в навигации Эдмонд Гюнтер в 1623 г (рис.12).

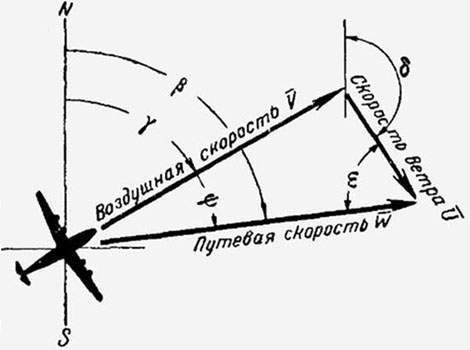
Рис.12 Эдмонд Гюнтер

Рис.13 Треугольник скоростей

Также тригонометрия помогает рассчитывать влияние ветра на полёт самолёта. Треугольник скоростей – это треугольник, образованный вектором воздушной скорости, вектором ветра и вектором путевой скорости (рис.13).

Для решения навигационного треугольника скоростей используются счетные устройства, использующие навигационную линейку и подсчеты в уме.

7.Тригонометрия в строительстве

Рис.14 Установка подходящих углов при постройке крыши

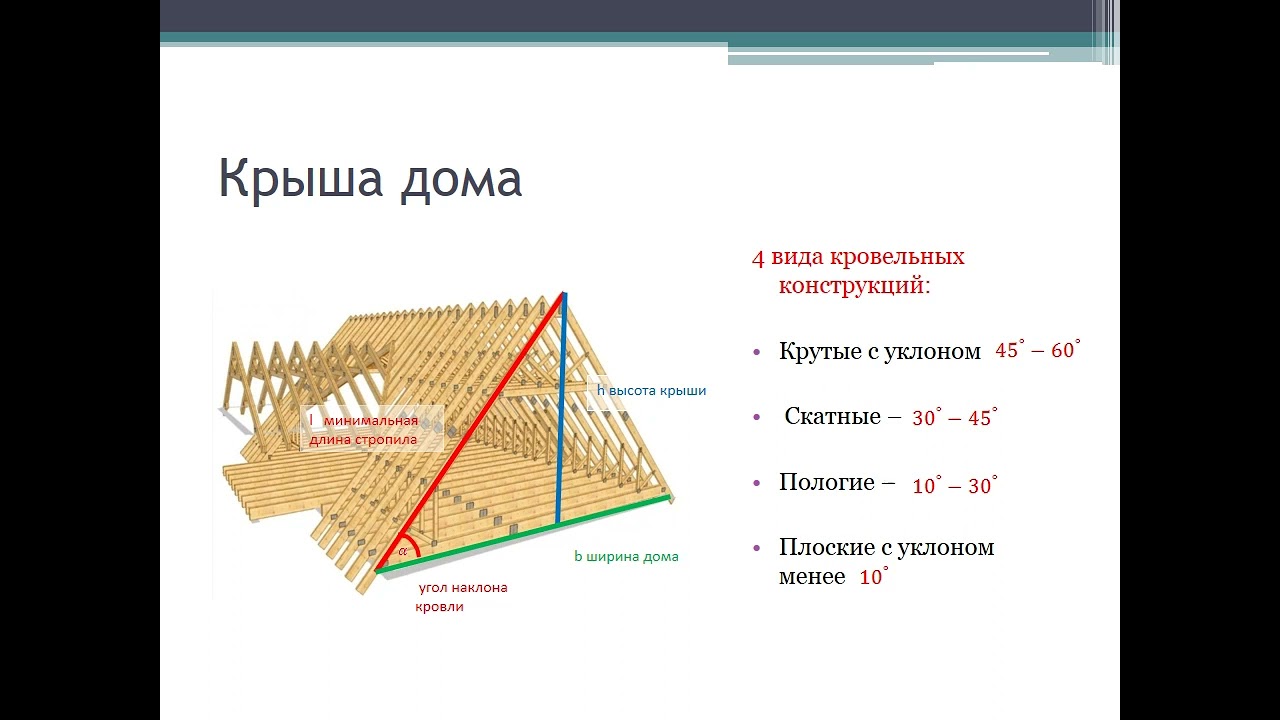
В строительстве специалисты полагаются на тригонометрию для расчета необходимых углов, чтобы эффективно и в достаточной степени соответствовать требованиям строительных норм. При регулировке уклона или наклона ландшафта, окружающего объект недвижимости, требуется установить его под подходящим углом (рис.14). Также нужно учитывать ещё многие нюансы. При малейших ошибках в чертежах строение может получиться ненадёжным и опасным для использования его человеком.

7.1Искуство и архитектура

Большинство композиционных решений и построений рисунков проходило именно с помощью геометрии. Но теоретические данные мало что значат. Рассмотрим пример построения одной скульптуры французского мастера Золотого века искусства.

Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой. Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности.

Велось множество расчетов, чтобы фигура с большой высоты смотрелась пропорционально. В основном они были основаны на методе визирования, то есть приблизительного измерения, на глаз. Однако коэффициент разности тех или иных пропорций позволили сделать фигуру более близкой к идеалу.

Т

аким образом, зная примерное расстояние от статуи до точки зрения, а именно от верха статуи до глаз человека и высоту статуи, можно рассчитать синус угла падения взгляда с помощью таблицы.

Рис.16 Феликс Кандела - Ресторан в Лос-Манантиалесе

Рис.15 Детская школа Гауди в Барселоне

Культовые здания во всем мире были спроектированы благодаря тригонометрии, которая может считаться гением архитектуры. Некоторые известные примеры таких зданий: Детская школа Гауди в Барселоне (рис 15), Ресторан в Лос-Манантиалесе в Аргентине (рис.16), мост в Сингапуре. При проектировании этих зданий не обошлось без тригонометрии.

Заключение

Изучив теоретические и прикладные аспекты тригонометрии, я поняла, что данная отрасль тесно связана со многими науками. Тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.

В настоящее время тригонометрические вычисления применяются практически во всех областях геометрии, физики, навигации, инженерного дела.

Знакомясь с ее влиянием в других областях, мы можем сделать вывод о том, что тригонометрия активно влияет на жизнедеятельность человека. Связь математики с окружающим миром позволяет «материализовать» знания школьников. Благодаря этому, мы можем адекватнее воспринять и усвоить знания и информацию, которую нам преподают в школе.

Список литературы

1. Глейзер Г.И. История математики в школе: IX-X кл. — М.: Просвещение, 1983.

2. Перельман Я.И. Занимательная алгебра, занимательная геометрия 2005.

3. https://ru.wikipedia.org/wiki/Ортопедия

4.https://fb.ru/article/211382/istoriya-trigonometrii-vozniknovenie-i-razvitie?ysclid=lp7472wt7o247321898

5. https://trigonometry23.tilda.ws/

6. https://studopedia.su/16_20720_dopolnitelnoe-primenenie-trigonometrii-v-zhizni.html

7. https://zaochnik.com/spravochnik/biologija/antropologija/bioritmy-cheloveka/

9