XII межрегиональный смотр – конкурс методических работ педагогов образовательных учреждений
Кировское областное государственное профессиональное образовательное автономное учреждение «Колледж промышленности и автомобильного сервиса»
Наименование работы
«Показательная функция. Уравнения и неравенства»
Номинация: «Учебное пособие»
Фамилия , имя, отчество авторов: Киселёва Ирина Ивановна,
Шулятьева Наталья Николаевна
Должность авторов: преподаватели математики
Контактный телефон: 8-919-512-80-98
Адрес электронной почты: [email protected]
Киров
2016
Киселёва И.И., Шулятьева Н.Н. Учебное пособие по дисциплине «Математика» для студентов 1 курса КОГПОАУ «КПиАС».
Киров, КОГПОАУ «КПиАС», 2016 г. 28 с.
Рецензент:
Демакова А.В., заведующтй учебно-методической работой КОГПОАУ СПО «Колледж промышленности и автомобильного сервиса»
Содержание
|
| стр. |
| Пояснительная записка | 4 |
| Глава 1. Показательная функция | 5 |
| Тема 1.1 Свойства и график показательной функции. | 5 |
| Тема 1.2 Графическое решение уравнений. | 8 |
| Тема 1.3 Графическое решение неравенств. | 9 |
| Задания для самоконтроля. | 9 |
| Глава 2. Показательные уравнения и неравенства. | 10 |
| Тема 2.1 Простейшие показательные уравнения. | 10 |
| Тема 2.2 Уравнения, решаемые способом введения новой переменной. | 12 |
| Тема 2.3 Уравнения, решаемые вынесением общего множителя за скобку. | 13 |
| Тема 2.4 Простейшие показательные неравенства. | 15 |
| Задания для самоконтроля. | 17 |
| Глава 3. Задания и упражнения для подготовки к письменному экзамену. | 17 |
| Задания для самоконтроля | 18 |
| Приложения | 19 |
| Заключение | 30 |
| Список литературы | 31 |
Пояснительная записка
Учебное пособие по дисциплине «Математика» по теме «Показательная функция. Уравнения и неравенства» составлено в соответствии с учебным планом и программой дисциплины.
Пособие содержит задачи репродуктивного, поискового характера, которые служат базой для дальнейшего изучения математики.
Учебное пособие содержит: таблицы, схемы, образцы и алгоритмы решений задач, что помогает обучающемуся самостоятельно изучить тему, не прибегая к помощи преподавателя, вопросы теории и справочный материал, вопросы для самоконтроля, методические рекомендации по выполнению проверочных работ, варианты заданий для проверочных работ, список рекомендуемой литературы. Учебное пособие предназначено для использования обучающимися с целью самостоятельного изучения учебной дисциплины, коррекции знаний при повторении и подготовке к зачету.
Глава 1. Показательная функция
Тема 1.1 Свойства и график показательной функции.
Определение1 : Функция вида 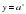 , где а0, и а≠1, называется показательной функцией.
, где а0, и а≠1, называется показательной функцией.
Свойства показательной функции:
Область определения показательной функции: D (y)=R – множество всех действительных чисел.
Область значений показательной функции: E (y)=R+ - множество всех положительных чисел.
Показательная функция y=aх возрастает при a1, показательная функция y=aх убывает при 0
Справедливы все свойства степенной функции:
а0=1 (любое число (кроме нуля) в нулевой степени равно единице).
а1=а (любое число в первой степени равно самому себе).
ах∙aу = aх+у (при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают).
ах:aу = aх-у (при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя первого множителя вычитают показатель второго).
(a х)у=aху (при возведении степени в степень основание оставляют прежним, а показатели перемножают).
(a∙b)х=aх∙bу (при возведении произведения в степень возводят в эту степень каждый из множителей).
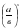 =
= 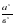 (при возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби).
(при возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби).
а-х = 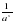 (при возведении числа в отрицательную степень число с положительным показателем переносят в знаменатель дроби, а в числителе ставят единицу).
(при возведении числа в отрицательную степень число с положительным показателем переносят в знаменатель дроби, а в числителе ставят единицу).
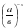 =
= 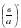 (при возведении дроби в отрицательную степень, числитель и знаменатель меняют местами и показатель становится положительным).
(при возведении дроби в отрицательную степень, числитель и знаменатель меняют местами и показатель становится положительным).
Пример1. Построить график функции y=2х.
Найдем значения функции при х=0, х=±1, х=±2, х=±3.
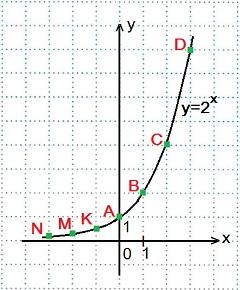
x=0, y=20=1; точка А.
x=1, y=21=2; точка В.
x=2, y=22=4; точка С.
x=3, y=23=8; точка D.
x=-1, y=2-1= 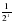 (см. свойство 11, далее - свойство5) =
(см. свойство 11, далее - свойство5) =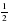 ; точка K.
; точка K.
x=-2, y=2-2= 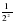 (см. свойство 11, далее - свойство5) =
(см. свойство 11, далее - свойство5) =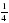 ; точка M.
; точка M.
x=-3, y=2-3= 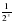 (см. свойство 11, далее - свойство5) =
(см. свойство 11, далее - свойство5) =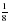 ; точка N.
; точка N.
а) Область определения функции : D (y)=R
б) Область значения: E (y)=R+
в) Промежутки возрастания и убывания: функция y=2х возрастает на всей области определения D (y)=R, так как основание функции 21
г) Промежутки, в которых функция принимает положительные и отрицательные значения: функция принимает только положительные значения (свойство 2)
д) Значение х, при котором у=0: нет таких значений
значение у, при котором х=0: у = 20 = 1
Пример2. Построить график функции y = 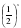 (аналогично примеру1)
(аналогично примеру1)
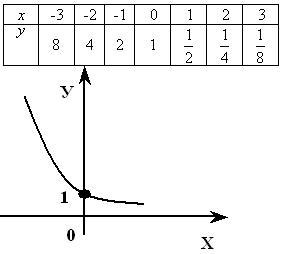
а) Область определения функции : D (y)=R
б) Область значения: E (y)=R+
в) Промежутки возрастания и убывания: функция y=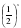 убывает на всей области определения D (y)=R, так как основание функции
убывает на всей области определения D (y)=R, так как основание функции 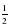
г) Промежутки, в которых функция принимает положительные и отрицательные значения: функция принимает только положительные значения (свойство 2)
д) Значение х, при котором у=0: нет таких значений
значение у, при котором х=0: у =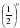 = 1
= 1
Задание № 1. Постройте график функции у=3 и запишите основные свойства функции по указанному алгоритму.
и запишите основные свойства функции по указанному алгоритму.
Составьте таблицу значений данной функции
Постройте эти точки в системе координат ХОУ и соедините плавной линией
Укажите:
а) Область определения функции D (x)
б) Область значения Е(у)
в) Промежутки возрастания и убывания
г) Промежутки, в которых функция принимает положительные и отрицательные значения
д) Значение х, при котором у=0; значение у, при котором х=0.
Задание № 2. Построить график функции у = 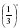 и записать основные свойства функции по указанному алгоритму.
и записать основные свойства функции по указанному алгоритму.
Составьте таблицу значений данной функции (при заполнении таблицы воспользуйтесь свойством 12, свойством 10)
Постройте эти точки в системе координат ХОУ и соедините плавной линией
Укажите:
а) Область определения функции D (x)
б) Область значения Е(у)
в) Промежутки возрастания и убывания
г) Промежутки, в которых функция принимает положительные и отрицательные значения
д) Значение х, при котором у=0; значение у, при котором х=0
Тема 1.2 Графическое решение уравнений.
Пример. Графически решить уравнение: 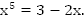
Решение: построим графики функций 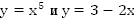 .
.
График функции 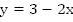 – прямая, построим её по таблице.
– прямая, построим её по таблице.
Графики пересекаются в точке  Других точек пересечения нет, т.к. функция
Других точек пересечения нет, т.к. функция  монотонно возрастает, функция
монотонно возрастает, функция 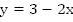 монотонно убывает, а, значит, их точка пересечения является единственной.
монотонно убывает, а, значит, их точка пересечения является единственной.
Ответ: 
Тема 1.3 Графическое решение неравенств.
Пример. Решить неравенство
a) 
б) 
Решение:
a) Чтобы выполнялось неравенство, график функции  должен располагаться над прямой
должен располагаться над прямой 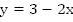 (см. рисунок). Это выполняется при
(см. рисунок). Это выполняется при 
б) В этом случае, наоборот, парабола  должна находиться под прямой. Это выполняется при
должна находиться под прямой. Это выполняется при 
Ответ: a)  б)
б) 
Задания для самоконтроля
| 1. Решить графически: 2. Расположить в порядке убывания: 3. Найти: а) наименьшее значение функции у=10х на [−2;5]; б) наибольшее целое значение функции у= на (−2;+); на (−2;+); | 1. Решить графически: 2. Расположить в порядке убывания:
 3. Найти: 3. Найти: а) наибольшее значение функции у=0,3х на [−1;6]; б) наибольшее целое значение функции у=9х на (−;1,5);
|
| в) произведение наибольшего и наименьшего значения функции у= ; ; г) количество целых значений функции у= ; ; д) область значений функции  ; ; е) наибольшее целое значение функции у=−0,09х−2· 0,3х+2. | в) сумму наибольшего и наименьшего значения функции у=5−2sinx+1; г) количество целых значений функции у= ; ; д) область значений функции  ; ; е) наименьшее целое значение функции у=25х+6·5х+4. |
Глава 2. Показательные уравнения и неравенства
Тема 2.1 Простейшие показательные уравнения.
Определение 2. Показательными называются уравнения, в которых неизвестная переменная находится только в показателях каких-либо степеней.
Для решения показательных уравнений требуется знать и уметь использовать следующую теорему:
Теорема: Показательное уравнение  (где а 0, а≠ 1) равносильно уравнению f(x) = g(x).
(где а 0, а≠ 1) равносильно уравнению f(x) = g(x).
Алгоритм решения простейшего показательного уравнения
| Алгоритм решения | Пример |
| Решить уравнение | 4х = 64 |
| Привести обе части данного уравнения к степеням с одинаковыми основаниями |
4х = 43 |
| Приравнять показатели | х = 3 |
| Записать ответ | Ответ: х= 3 |
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1
2x = 16
2x = 24
x = 4
Пример 2
2x+3 = 64
2x+3 = 26
x+3 = 6
x = 3
Пример 3
0,5x = 0,125
0,5x = 0,53
x = 3
Пример 4
3-8-x = 9
3-8-x = 32
-8-x = 2
-x = 2+8
-x = 10
x = -10
Решите самостоятельно:
1) 5x = 25
2) 3x = 27
3) 4x = 64
4) 5x-7 = 125
5) 37-x = 27
6) 4-6-x = 4
7)( )x =
)x = 
8) 0,1x = 0,001
9) 0,2x-3 = 0,04
10) ( )x+5 =
)x+5 = 
11) ( )x-4 =
)x-4 = 
12) 5x = 25√5
Решение показательных уравнений, содержащих дробь в одной из частей
Пример 1  =
= 
 =
= 
 =
= 
 =
=  =
= 
х = -2  =
=  =
= 
Пример 2  = 9
= 9
 =
= 
 =
= 
 =
= 
 =
= 
-х = 2  =
= 
х = -2
Пример 3  = 4
= 4 
 =
=  *
* 
 =
= 
-х = 2
х = -2
Решите уравнения
а)  б)
б) 
в)  г)
г)  =81
=81
д)  е)
е) 
ж) 5 з) 2
з) 2
Тема 2.2 Уравнения, решаемые способом введения новой переменной.
Показательные уравнения, приводимые к квадратным уравнениям:
 t 0
t 0
пусть  = t , тогда
= t , тогда  =
= =
=
 - 5t + 4 = 0
- 5t + 4 = 0 
D = 9  = 4
= 4  = 1
= 1
Переходим к исходным переменным. И решаем два простейших показательных уравнения:
 = 4
= 4  = 1
= 1
x = 2 x = 0
Ответ: x1 = 2; x2 = 0.
Решите показательные уравнения, приводимые к квадратным
а) 
б) 
Тема 2.3 Уравнения, решаемые вынесением общего множителя за скобку
Пример 
 +
+ = 130
= 130
 ·
·  +
+  = 130
= 130
 (
( +1) = 130
+1) = 130
 (25+1) = 130
(25+1) = 130
 =
= 
 = 5
= 5
 =
= 
х = 1
Показательные уравнения (различные способы решения)
Пример 1  -5·
-5· -88=0
-88=0
t0  ·
· -5
-5 -88=0
-88=0
пусть  =t, тогда
=t, тогда  =
= =
=
 -5t-88=0
-5t-88=0
D= 25+8·88=729
 =
= =8
=8
 =
= =
= -постор. корень, т.к. t0
-постор. корень, т.к. t0

 =8 x= 3
=8 x= 3
Пример 2  -
- - 32=0
- 32=0
 =
= =4
=4  = t
= t
 -4t-32=0
-4t-32=0
D=144
 =8
=8
 =8
=8  =-4 -постор. корень
=-4 -постор. корень
 x= -3
x= -3
Пример 3 3· +
+ -2·
-2· =0
=0
3· +
+ – 2·
– 2· =0 | :
=0 | : 
3+ -2·
-2· = 0
= 0
t=
Самостоятельно: 1) 52х+1-26 ·5х+5 = 0;
2) 


3) 2· ;
;
4) 3 ;
;
5) 5·
Тема 2.4 Простейшие показательные неравенства.
Определение 3. Неравенства, которые содержат переменную в показателе степени, называются показательными.
Показательные (простейшие) неравенства – правила решения

Если a 1, то знак между показателями не меняем: x y
Если a - число, меньшее 1, то знак между показателями меняем на противоположный:
x y
Пример 1 

 5
5
X
Ответ: (-∞; 5)
Пример 2  ≥
≥ 

0 ≥  5
5
Знак меняем! X ≥ 5
Ответ: (-∞; 5)
Пример 3 0, ≤
≤ 

 ≤
≤  2
2
X ≥ 2
Ответ: [ 2 ; +∞)
Самостоятельно: а) 2х≥4; б) 2х˃ ; в) 3х≤81; г)
; в) 3х≤81; г) 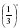 ˃
˃ ; д) 32х-4≤27; е)
; д) 32х-4≤27; е)  ˃
˃ ;
;
ж) 45х-1˃163х+2; з)  ≥
≥ ; и) 23х+6≤
; и) 23х+6≤ ; к)
; к)  ˃
˃ .
.
Ниже приведена краткая схема решения простейших показательных неравенств
| a1 | 0 a |
| 
х1 х2 | 
 
|
|  ↔ х1х2 ↔ х1х2
|  ↔ х1х2 ↔ х1х2
|
| Пример:  Решение:  | Пример:  Решение: 
|
| Т. к. а1 то в силу возрастания показательной функции х4 | Т. к. 0 х
|
| 
х 4 | 
4 х |
| Ответ:(4,+∞) | Ответ:(- ∞,4) |
Решите следующие показательные неравенства.
а) 
б) 
в) 
г) 

Упражнения (решение уравнений) для подготовки к экзамену и ЕГЭ
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
9)  Делим на
Делим на  .
.
; .
 .
.
 .
.
 .
.
 .
.

 .
.




 .
.
 .
.
 ,
,
 .
.
 .
.
 .
.






 .
.
 .
.

Глава 3. Упражнения (решение неравенств) для подготовки к экзамену и ЕГЭ
≤
 .
.
≤
 .
.
≤
 .
.
≤
 .
.
 .
.

 .
.




 .
.
 .
.
 ,
,
 .
.
 .
.
 .
.






 .
.
 .
.

Приложения
1. Справочные материалы
Формулы сокращенного умножения
Действия со степенями



Действия с дробными степенями и корнями



Абсолютная величина действительного числа
Абсолютной величиной или модулем действительного числа x называется само число x, если оно не отрицательное, т.е.

Квадратное уравнение
Уравнение вида  , где a,b,c – некоторые числа, причем
, где a,b,c – некоторые числа, причем  ; x – искомая переменная, называется квадратным уравнением.
; x – искомая переменная, называется квадратным уравнением.
Дискриминантом квадратного уравнения называется число  .
.
Если D = 0, то уравнение имеет два совпадающих корня (единственное решение):
 .
.
Если D 0, то уравнение имеет два различных действительных корня:
 .
.
Если D
Теорема Виета (прямая) утверждает: если квадратное уравнение  имеет корни x1 и x2, то выполняются соотношения
имеет корни x1 и x2, то выполняются соотношения 
Левая часть квадратного уравнения называется квадратным трехчленом, число D – его дискриминантом, а x1 и x2 – корнями трехчлена.
Трехчлен может быть разложен на множители следующим образом:
а) если D 0, то  ;
;
б) если D = 0, то  .
.
Функция вида  называется квадратичной функцией, ее графиком является парабола. Расположение параболы в системе координат определяется значениями коэффициентов a,b,c:
называется квадратичной функцией, ее графиком является парабола. Расположение параболы в системе координат определяется значениями коэффициентов a,b,c:
а) вершина параболы расположена в точке с абсциссой  , а прямая
, а прямая  является осью симметрии параболы;
является осью симметрии параболы;
б) знак числа a показывает, куда направлены ветви параболы – если  , то вверх, если
, то вверх, если  , то вниз.
, то вниз.
2. Тесты
Тест 1
1) корнем к – й степени из числа а называется такое число ….(закончить предложение)
2) Арифметическим корнем к – й степени из числа а называется такое … число, к –я степень которого равна а (где к – натуральное) (вставить пропущенное слово)
3) Произведение  равно
равно
А) 3;
Б) 4;
В) - 3;
Г) 2
4)  =
=
А) 6;
Б) -6;
В) ±6;
Г) 10
5) Выражение

А) Не имеет значения
Б) Имеет одно значение
В) Имеет два значения
Г) Имеет бесконечно много значений.
6) Степенью с рациональным показателем называется число:
А)  =
=
Б) 

В)  =
=
Г)  =
=
7) 5º=
А)5
Б) 1
В)0
Г) нет значения
8) Функция у= является
является
А) Возрастающей на всей области определения
Б) Убывающей на всей области определения
В) Возрастающей при х0
Г) Убывающей при х0
9) Решением уравнения 
А) 3
Б) 4
В) 9
Г) 2
10) Неравенство  равносильно неравенству х…2 (вставить пропущенный знак)
равносильно неравенству х…2 (вставить пропущенный знак)
Ответы на вопросы теста 1:
1). …к-ая степень которого равна числу а.
2). …неотрицательное…
3). А)
4). Б)
5). А)
6). А)
7). Б)
8). А)
9). Б)
10).
Критерий оценки
0 – неправильных ответов - 5
1-2- неправильных ответов – 4
3 – 4 – неправильных ответов – 3
Более четырёх неправильных ответов - 2
Тест 2
Вариант 1
По теме «Показательная функция. Показательные уравнения»
График какой из перечисленных функций изображен на рисунке:
1)
Какое из следующих чисел входит в область значений функции  .
.

Найдите область определения функции 

Решить уравнение:  .
.
Укажите промежуток, которому принадлежит корень уравнения:  .
.

Сравните числа: а) 
Укажите промежуток, которому принадлежит корень уравнения 

Найдите сумму корней уравнения: 
1) 1; 2) 2; 3) -2; 4) 50.
9. Решите уравнение: 
Найдите решение  системы уравнений
системы уравнений  и вычислите произведение
и вычислите произведение 
Ответы на вопросы теста 2 (1 вариант):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 3 | 2 | 2 | -2,5 | 3 | а) ;б ;б | 2 | 3 | 3 | 6 |
Вариант 2
По теме «Показательная функция. Показательные уравнения»
1.График какой из перечисленных функций изображен на рисунке:
1)
2. Укажите наименьшее целое число, входящее в множество значений функции  .
.

3. Найдите область определения функции 
4. Решить уравнение:  .
.
5. Укажите промежуток, которому принадлежит корень уравнения:  .
.

6. Сравните числа: а) 
7. Укажите промежуток, которому принадлежат корни уравнения 

8. Найдите произведение корней уравнения: 
1) -6; 2) -4; 3) 4; 4) 6.
9. Решите уравнение: 
10. Найдите решение  системы уравнений
системы уравнений  и вычислите сумму
и вычислите сумму 
Ответы на вопросы теста 2 (2 вариант):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 4 | -1 | 2 | -3 | 3 | а ;б) ;б) | 3 | -6 | 1,8 | 1 |
Вариант 3
По теме «Показательная функция. Показательные уравнения»
1. График какой из перечисленных функций изображен на рисунке:
1)
2. Укажите наибольшее число, входящее в область значений функции  .
.

3. Найдите область определения функции 
4. Решить уравнение:  .
.
Укажите промежуток, которому принадлежит корень уравнения:  .
.

Сравните числа: а)
Укажите промежуток, которому принадлежат корни уравнения -- 

Найдите произведение корней уравнения: 
1) 
9. Решите уравнение: 
10. Найдите решение  системы уравнений
системы уравнений  и вычислите произведение
и вычислите произведение 
Ответы на вопросы теста 2 (3 вариант):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 1 | 1 | 0,2 | 2 | а ;б) ;б) | 2 | 2 | 1,1 | 0,9375 |
Вариант 4
По теме «Показательная функция. Показательные уравнения»
1. График какой из перечисленных функций изображен на рисунке:
1)
2. Какое из следующих чисел входит в область значений функции  .
.

3. Найдите область определения функции 
4. Решить уравнение:  .
.
Укажите промежуток, которому принадлежит корень уравнения:  .
.

Сравните числа: а)
Укажите промежуток, которому принадлежат корни уравнения 

Найдите произведение корней уравнения: 

9. Решите уравнение: 
10. Найдите решение  системы уравнений
системы уравнений  и вычислите произведение
и вычислите произведение 
Ответы на вопросы теста 2 (4 вариант):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 3 | 4 | 2,4 | 4 | а ;б) ;б) | 4 | 2 | 1 | 0 |
3. Контрольная работа
1. Вычислите: а)  .
.
Г) :  .
.
2. Найдите значение числового выражения: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
3. Найдите значение выражения  при
при
 .
.
4. Решите уравнение: а) ; б)
; б)  .
.
5. Решите неравенство  .
.
6. Постройте графики следующих функций и опишите их свойства.
а) 
б) 
Критерий оценки:
95 -100% - выполнения задания оценка «5»
75 – 94% выполнения задания оценка «4»
60 -74% выполнения задания оценка «3»
Ниже 60% выполнения задания оценка «2»
Заключение
Учебное пособие «Показательная функция, Уравнения и неравенства» может быть использовано преподавателями образовательных организаций СПО для студентов 1 курса. Данное пособие предназначено для внеаудиторной самостоятельной работы, проверки и коррекции знаний студентов.
Литература
Для студентов
1. Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2014.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2014.
4.Башмаков М.И. Математика. Сборник задач профильной направленности: учеб. пособие для студ. учреждений сред. проф. образования. — М., 2014.
Дополнительные источники:
Колмогоров А.Н. и др. Алгебра и начала математического анализа: учебник для 10 – 11 кл. общеобразоват. учрежд., 17 изд., – М.: Просвещение, 2008.
Математика. 11 класс: учеб. для учащихся общеобразоват. учреждений (базовый уровень) / [А. Г. Мордкович, И. М. Смирнова, П. В. Семенов и др.]; под ред. А. Г. Мордковича, И. М. Смирновой. – 5-е изд., стер. – М.: Мнемозина, 2010.
Мордкович А. Г. Алгебра и начала анализа. 10 класс. В 2 ч. Ч 1: учебник для общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. – 4-е изд., доп. – М.: Мнемозина, 2007.
Погорелов А. В. Геометрия: Учеб. для 10 – 11 кл. общеобразоват. учреждений / А. В. Погорелов. – 4-е изд., доработ. – М.: Просвещение, 2011.
Для преподавателей
1. Федеральный закон от 29.12.2012 № 273-ФЗ «Об образовании в Российской Федерации». Приказ Министерства образования и науки РФ от 17.05.2012 № 413 «Об утверждении федерального государственного образовательного стандарта среднего (полного) общего образования».
2. Приказ Министерства образования и науки РФ от 29.12.2014 № 1645 «О внесении изменений в Приказ Министерства образования и науки Российской Федерации от 17.05.2012 № 413 «“Об утверждении федерального государственного образовательного стандарта среднего (полного) общего образования”».
Интернет-ресурсы
| http://mon.gov.ru/ http://www.edu.ru http://www.fipi.ru
| http://ege.edu.ru http://www.school.edu.ru http://pedsovet.alledu.ru http://www.it-n.ru/ http://www.openclass.ru http://www.vestnik.edu.ru/ |
5






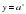 , где а0, и а≠1, называется показательной функцией.
, где а0, и а≠1, называется показательной функцией.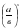 =
= 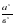 (при возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби).
(при возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби).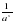 (при возведении числа в отрицательную степень число с положительным показателем переносят в знаменатель дроби, а в числителе ставят единицу).
(при возведении числа в отрицательную степень число с положительным показателем переносят в знаменатель дроби, а в числителе ставят единицу).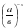 =
= 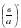 (при возведении дроби в отрицательную степень, числитель и знаменатель меняют местами и показатель становится положительным).
(при возведении дроби в отрицательную степень, числитель и знаменатель меняют местами и показатель становится положительным).
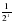 (см. свойство 11, далее - свойство5) =
(см. свойство 11, далее - свойство5) =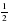 ; точка K.
; точка K.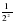 (см. свойство 11, далее - свойство5) =
(см. свойство 11, далее - свойство5) =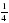 ; точка M.
; точка M.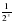 (см. свойство 11, далее - свойство5) =
(см. свойство 11, далее - свойство5) =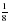 ; точка N.
; точка N.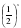 (аналогично примеру1)
(аналогично примеру1)
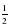
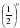 = 1
= 1 и запишите основные свойства функции по указанному алгоритму.
и запишите основные свойства функции по указанному алгоритму.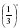 и записать основные свойства функции по указанному алгоритму.
и записать основные свойства функции по указанному алгоритму.









