Тема: Умножение положительных и отрицательных чисел.
Цель: ввести правила умножения двух отрицательных чисел и чисел с разными знаками; развивать правильную математическую речь; формирование внутренних процессов интеллектуального, личностного, эмоционального развития.
Ход урока
Организационный момент
«Математика – это больше, чем наука, это язык» (Н. Бор)
Устный счёт
Вычисли: -3+11 Л; -9+(-6) А; 8+(-10) В; -5-7 К; 1,2+(-0,8) Ю; 0,7+(-2) Л; -0,4-0,6 Й; -0,2-(-5) Ь; (-0,1)+(-0,02) Ь; -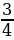 +0,25 Я; -2,08-0 Я; -
+0,25 Я; -2,08-0 Я; -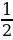 +0,5 Л
+0,5 Л
Расположите получившиеся ответы в порядке убывания и прочитайте название самого большого вулкана на планете
| 8 | 4,8 | 0,8 | 0 | -0,12 | -0,5 | -1 | -1,3 | -2 | -2,08 | -12 | -15 |
| Л | Ь | Ю | Л | Ь | Я | Й | Л | Ь | Я | К | А |
Представьте данную сумму в виде произведения
а +a +а +а +а +а +а +а +а; -n–n-n-n-n-n-n; -4х-4х-4х-4х-4х; (в-2с) + (в-2с) + (в-2с).
Представьте в виде суммы произведения и найдите их значения
4 · 2; -3 · 3; -23 · 2; 4 · (-5); -283 · 40.
Когда ребята дошли до решения последнего примера, то возникла проблема: данное произведение неудобно представить в виде суммы и сосчитать.
Сообщение темы и цели урока
Учитель: Что же мы должны на уроке придумать?
Ответ: Придумать правило на умножение положительных и отрицательных чисел.
Учитель: Правильно. Молодцы. Таким образом, мы с вами переходим к теме урока, которую вы можете сформулировать…
Ответ: Умножение положительных и отрицательных чисел.
После того как совместными усилиями определена и сформулирована тема урока учитель записывает её на доске, а учащиеся в своих тетрадях.
Учитель: А какова цель урока?
Ответ: Научиться умножать положительные и отрицательные числа.
Изучение нового материала
Учитель: Для того чтобы научиться умножать положительные и отрицательные числа нам надо знать правило по которому мы будем действовать. Попытайтесь это сделать.
Учащиеся дают определение правила умножения с разными знаками и проверяют его на примерах.
Правило. При умножении чисел с разными знаками:
перемножить модули этих чисел;
перед полученным числом поставить знак минус.
Например: -0,5·7=-3,5; 0,5·(-7)=-3,5; 0,5·7=3,5
Учитель: Какой вывод можно сделать?
Ответ: При изменении знака любого множителя знак произведения меняется, а его модуль остаётся тем же.
Учитель: А как же нам быть, если -0,5·(-7)?
Ответ: В данном произведении знаки меняются у обоих множителей, следовательно, и произведение дважды меняет знак. Получится 3,5.
Учитель: Какой вывод можно сделать?
Ответ: Произведение отрицательных чисел есть число положительное.
Учитель: Послушайте, как рассуждал при решении этого примера русский математик швейцарского происхождения Леонард Эйлер: «Зная, что -2·2=-4, следует, что при произведении -2 на -2 не может получиться 4. Таким образом может быть только 4».
Учитель: Сформулируйте правило умножения отрицательных чисел.
Учащиеся дают определение правила умножения отрицательных чисел.
Правило. При умножении двух отрицательных чисел:
перемножить модули этих чисел;
перед полученным числом поставить знак плюс.
Например: -1,5·(-3)=1,5·3=4,5; -2,3·(-2)=4,6; -0,3·(-7)=2,1.
Учитель: Правило знаков можно истолковать и таким образом:
| (+) · (+) = (+) | «Друг моего друга – мой друг» |
| (-) · (-) = (+) | «Враг моего врага – мой друг» |
| (+) · (-) = (-) | «Друг моего врага – мой враг» |
| (-) · (+) = (-) | «Враг моего друга – мой враг» |
Закрепление изученного материала
№ 1121 (1,2 столбик) – устно
№ 1121 (3 столбик) – письменно в тетрадях и на доске
самостоятельно (расположить в порядке убывания)
| Задание «А» | Задание «В» |
| - 2 · 9 | Э | - 0,5 · 40 | Р |
| - 4 · 15 | Д | - 0,1 · (- 3) | К |
| 12 · (- 7) | Р | 0,9 · (- 0,6) | С |
| - 45 · (- 1) | О | 0,04 · (- 10) | О |
| - 8 · (- 0,7) | К | - 1 · 3,2 | Д |
| 0 · (-7,4) | А | - 10 · 0,1 | А |
| 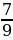 · 3 · 3
| Т | 3,6 · 2 | И |
|
|
| 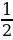 · (- 4) · (- 4)
| Э |
Учитель: Проверим, какие слова у вас получились. Если вычисления сделаны правильно, то должны получиться слова «октаэдр», «икосаэдр» - это названия правильных многогранников в пространстве.
Физкультминутка
Повторение ранее изученного материала
Блиц-опрос
Сумма двух отрицательных чисел есть число… (отрицательное)
Сумма двух противоположных чисел равна… (нулю)
При сложении двух чисел с разными знаками знак суммы совпадает со знаком того слагаемого, модуль которого… (больше)
Чтобы из одного числа вычесть другое число надо… (к уменьшаемому прибавить число, противоположное вычитаемому)
Чтобы найти расстояние между двумя точками на координатной прямой, надо найти модуль… (разности координат соответствующих точек)
Самостоятельная работа (5-7 минут)
| Выполните умножение |
| Вариант I | Вариант II |
| 10 · (- 3,9) | 10 · (-6,3) |
| - 100 · 7,4 | -10 · 3,1 |
| - 65 · (-10) | -25 · (- 100) |
| - 2 · 2,4 | - 4 · 1,4 |
| 2 · (- 2,9) | 2 · (- 3,2) |
| - 5 · 1,2 | - 5 · 1,8 |
| - 1,5 · (- 3) | - 1,7 · (- 3) |
| - 4 · 1,6 | - 6 · 1,2 |
Подведение итогов урока
Сформулируйте правило умножения двух чисел с разными знаками.
Как перемножаются два отрицательных числа?
Домашнее задание
Учебник стр. 192 прочитать текст под рубрикой «Говори правильно»
№ 1143 (а - г), № 1144 (а, б), № 1145 (а, г), № 1146.
| Выполните умножение |
| Вариант I | Вариант II |
| 10 · (- 3,9) | 10 · (-6,3) |
| - 100 · 7,4 | -10 · 3,1 |
| - 65 · (-10) | -25 · (- 100) |
| - 2 · 2,4 | - 4 · 1,4 |
| 2 · (- 2,9) | 2 · (- 3,2) |
| - 5 · 1,2 | - 5 · 1,8 |
| - 1,5 · (- 3) | - 1,7 · (- 3) |
| - 4 · 1,6 | - 6 · 1,2 |
| Выполните умножение |
| Вариант I | Вариант II |
| 10 · (- 3,9) | 10 · (-6,3) |
| - 100 · 7,4 | -10 · 3,1 |
| - 65 · (-10) | -25 · (- 100) |
| - 2 · 2,4 | - 4 · 1,4 |
| 2 · (- 2,9) | 2 · (- 3,2) |
| - 5 · 1,2 | - 5 · 1,8 |
| - 1,5 · (- 3) | - 1,7 · (- 3) |
| - 4 · 1,6 | - 6 · 1,2 |
самостоятельно (расположить в порядке убывания)
| Задание «А» | Задание «В» |
| - 2 · 9 | Э | - 0,5 · 40 | Р |
| - 4 · 15 | Д | - 0,1 · (- 3) | К |
| 12 · (- 7) | Р | 0,9 · (- 0,6) | С |
| - 45 · (- 1) | О | 0,04 · (- 10) | О |
| - 8 · (- 0,7) | К | - 1 · 3,2 | Д |
| 0 · (-7,4) | А | - 10 · 0,1 | А |
| 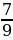 · 3 · 3
| Т | 3,6 · 2 | И |
|
|
| 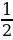 · (- 4) · (- 4)
| Э |
самостоятельно (расположить в порядке убывания)
| Задание «А» | Задание «В» |
| - 2 · 9 | Э | - 0,5 · 40 | Р |
| - 4 · 15 | Д | - 0,1 · (- 3) | К |
| 12 · (- 7) | Р | 0,9 · (- 0,6) | С |
| - 45 · (- 1) | О | 0,04 · (- 10) | О |
| - 8 · (- 0,7) | К | - 1 · 3,2 | Д |
| 0 · (-7,4) | А | - 10 · 0,1 | А |
| 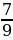 · 3 · 3
| Т | 3,6 · 2 | И |
|
|
| 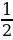 · (- 4) · (- 4)
| Э |
Вычисли: -3+11 Л; -9+(-6) А; 8+(-10) В; -5-7 К; 1,2+(-0,8) Ю; 0,7+(-2) Л; -0,4-0,6 Й; -0,2-(-5) Ь; (-0,1)+(-0,02) Ь; -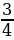 +0,25 Я; -2,08-0 Я; -
+0,25 Я; -2,08-0 Я; -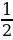 +0,5 Л
+0,5 Л
Расположите получившиеся ответы в порядке убывания и прочитайте название самого большого вулкана на планете
1 .Вычисли: -3+11 Л; -9+(-6) А; 8+(-10) В; -5-7 К; 1,2+(-0,8) Ю; 0,7+(-2) Л; -0,4-0,6 Й; -0,2-(-5) Ь; (-0,1)+(-0,02) Ь; -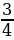 +0,25 Я; -2,08-0 Я; -
+0,25 Я; -2,08-0 Я; -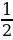 +0,5 Л
+0,5 Л
Расположите получившиеся ответы в порядке убывания и прочитайте название самого большого вулкана на планете







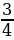 +0,25 Я; -2,08-0 Я; -
+0,25 Я; -2,08-0 Я; -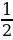 +0,5 Л
+0,5 Л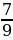 · 3
· 3









