Россия, с. Абатское
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 19.12.2022 15:21
Коняхина Екатерина Васильевна
Учитель начальных классов
35 лет
126 370
107 
Местоположение
Специализация
Урок 6. ДВУЗНАЧНЫЕ ЧИСЛА И ИХ ЗАПИСЬ.
Категория:
Математика
29.03.2019 04:51
Просмотр содержимого документа
«Урок 6. ДВУЗНАЧНЫЕ ЧИСЛА И ИХ ЗАПИСЬ.»
Урок 6. Двузначные числа и их запись
| Цели деятельности учителя | Создать условия для ознакомления учащихся с римскими цифрами; совершенствовать вычислительные навыки; способствовать развитию умения строить и читать математические графы; рассмотреть решение задачи разными способами; развивать умение сравнивать и рассуждать |
| Тип урока | Постановка и решение учебной задачи |
| Планируемые | Предметные (объем освоения и уровень владения компетенциями): научатся: записывать цифрами двузначные числа; решать составные арифметические задачи в два действия в различных комбинациях; вычислять сумму и разность чисел в пределах 100, используя изученные устные и письменные приемы вычислений; распознавать геометрические фигуры (многоугольники, окружность, прямоугольник, угол); получат возможность научиться: выполнять несложные устные вычисления в пределах 100. Метапредметные (компоненты культурно-компетентностного опыта/приобретенная компетентность): познавательные – устанавливать закономерности; использовать знаково-символические средства, в том числе модели (фишки), для решения задач; коммуникативные – адекватно использовать речевые средства для решения различных коммуникативных задач; строить монологическое высказывание; регулятивные – удерживать цель деятельности до получения ее результата. Личностные: проявлять терпение и доброжелательность в споре (дискуссии), доверие к собеседнику (соучастнику деятельности) |
| Методы и формы обучения | Объяснительно-иллюстративный; индивидуальная, фронтальная |
Организационная структура урока
| Этапы урока | Обучающие | Деятельность учителя | Деятельность | Формы | Универсальные | Форма |
| I. Актуализация знаний | Устный счет в игровой форме | Организует устный счет с целью актуализации знаний. • Сколько всего отрезков на чертеже?
• Помогите Незнайке найти ошибки. 8 + 6 = 14 7 + 9 = 16 4 + 8 = 13 12 – 4 = 7 16 – 8 = 8 13 – 6 = 7 6 + 7 = 12 8 + 5 = 12 9 + 9 = 18 • У кого масса меньше – у собаки или у кошки?
• Решите задачу. На свой день рождения Мальвина испекла пирожки и положила их на тарелку. После того как все гости взяли по одному пирожку, на тарелке осталось 8 пирожков. Сколько гостей пригласила Мальвина, если на тарелке было 17 пирожков?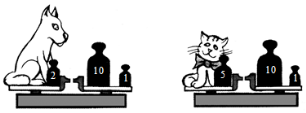
| Отвечают на вопросы учителя по материалу предыдущего Выполняют задания на формирование навыка устного счета | Фронтальная | Личностные: осознают Познавательные: общеучебные – извлекают необходимую информацию из рассказа учителя; логические – дополняют и расширяют имеющиеся знания и представления | Устные ответы |
| II. Сообщение темы урока | Сообщение темы урока. Определение целей урока | Задаёт вопросы. Комментирует ответы, предлагает сформулировать цель урока. – Прочитайте тему урока на доске. – Определите цели урока, используя опорные слова (см. с. 6). – Сегодня на уроке узнаем, как люди научились записывать числа | Обсуждают тему урока. Формулируют цель урока | Фронтальная | Регулятивные: определяют тему и цели урока. Коммуникативные: | Устные ответы |
| III. Изучение нового материала | Работа по учебнику. Задание 10 (с. 14) | Организует работу по теме урока. Объясняет новый материал, отвечает на вопросы учеников. – Какие числа называются однозначными? Двузначными? – Назовите разряды двузначного числа. – Какие двузначные числа можно записать цифрами 0, 2 и 4, если цифры в записи числа не повторяются? Запись: 20, 40, 24, 42. – Что такое цифра? Что такое число? – Сколько цифр вы знаете? – Сколько чисел в математике? Можете ли вы назвать наибольшее число? | Выполняют дидактические упражнения, отвечают на вопросы, высказывают свое мнение | Индивидуальная, фронтальная | Личностные: осознают Познавательные: общеучебные – умеют ориентироваться в учебнике; логические – сравнивают объекты по нескольким основаниям; находят закономерности; самостоятельно продолжают их по установленному правилу; осуществляют выбор оснований и критериев для сравнения объектов; подведение под понятие. Регулятивные: самостоятельно организуют свое рабочее место. Коммуникативные: участвуют в диалоге; слушают и понимают других | Устные ответы. Выполнение задания в рабочей тетради |
| Задание 11 (с. 14) | – С помощью каких цифр необходимо записать все возможные двузначные числа? (5 и 1.) Запись: 55, 51, 11, 15 | Записывают двузначные числа | Фронтальная, индивидуальная | Выполнение задания в тетради | ||
| Задание 12 (с. 14) | – Сколько всего двузначных чисел, запись которых оканчивается цифрой 5? (Девять цифр.) Запись: 15, 25, 35, 45, 55, 65, 75, 85, 95. – Сколько всего двузначных чисел, запись которых оканчивается цифрой 0? (Девять цифр.) Запись: 10, 20, 30. 40, 50, 60, 70, 80, 90 | Отвечают на вопросы, записывают числа | Фронтальная, индивидуальная | Выполнение задания в тетради | ||
| IV. Путешествие | Анализ занимательного материала по теме урока | Учитель и заранее подготовленные ученики рассказывают прочитанное по теме «Как люди научились записывать числа». – Сегодня мы отправимся в путешествие в Древний Египет, Индию, Вавилон и узнаем, как записывали цифры и числа разные народы (см. ресурсный материал) | Слушают сообщение | Индивидуальная, фронтальная | Личностные: проявляют интерес к истории математики. Познавательные: общеучебные – определяют круг своего незнания | Наблюдение |
| V. Первичное осмысление и закрепление | Работа по учебнику. Задание 22 | Задаёт вопросы. Комментирует ход решения. – Рассмотрите чертеж. Сколько точек на чертеже? (Три точки.) – Измерьте расстояние между каждыми двумя точками на чертеже. (3 см, 4 см, 5 см.) | Измеряют расстояние между двумя точками | Индивидуальная | Личностные: осознают успехи с усилиями, трудолюбием. Познавательные: общеучебные – отвечают на простые и сложные вопросы учителя, сами задают вопросы, находят нужную информацию Регулятивные: прогнозируют результаты уровня усвоения изучаемого материала; используют в работе простейшие инструменты; корректируют выполнение задания в дальнейшем; оценивают свое задание по следующим параметрам: легко выполнять, возникли сложности при выполнении. Коммуникативные: участвуют в диалоге; выполняют различные роли в группе, сотрудничают в совместном решении проблемы (задачи) | Выполнение задания в тетради |
| Задание 24 | – Какую фигуру называют треугольником? – Сколько треугольников на каждом рисунке?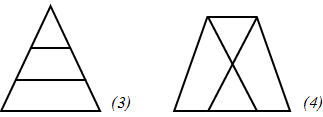
– Покажите на рисунках, как вы рассуждали.
Всего 3 треугольника.
Всего 4 треугольника | Находят треугольники на чертеже | Фронтальная, индивидуальная | Устные ответы | ||
| Задание 25 (с. 18) | – Какие следующие три числа надо записать в данном числовом ряду? 5, 10, 15, 20, … , … , … – Сравните каждые два соседних числа. (Закономерность: каждое следующее число на 5 больше предыдущего, поэтому дальше будут следовать числа: 25, 30, 35.) | Объясняют закономерность | Фронтальная, индивидуальная | Выполнение задания в тетради | ||
| Задание 26 (с. 18) | – Прочитайте условие задачи. – Мог ли остаться хоть один большой конверт без марки? – Мог ли остаться хоть один маленький конверт без марки? – На какие конверты могли наклеить марки? Рассмотрите все варианты.
| Решают комбинаторную | Фронтальная, индивидуальная | Выполнение задания в тетради | ||
| Работа в печатной тетради № 1. Задание 10 | Вероятнее всего, учащиеся предложат решать задачу более длинным путем, который естественно вытекает из ее условия:
– Проанализируйте текст задачи. Есть ли в задаче «лишнее» данное? Если есть, подчеркните его. Решение: 1) Сколько пассажиров осталось в автобусе после того, как вышли 10 человек? 20 – 10 = 10 (чел.). 2) Сколько пассажиров стало в автобусе после того, как вошли 8 человек? 10 + 8 = 18 (чел.). 3) На сколько человек уменьшилось число пассажиров автобуса? 20 – 18 = 2 (чел.). Этот способ решения учитель разбирает с учащимися устно, затем проводит беседу: – Сколько человек вышло на остановке? (10 чел.) А сколько вошло? (8 чел.) Уменьшилось или увеличилось число пассажиров автобуса? (Уменьшилось.) На сколько человек меньше вошло, чем вышло? Является ли ответ на этот вопрос ответом на вопрос задачи? – Как же решить эту задачу проще? Решение: 10 – 8 = 2 (чел.). Ответ: на 2 человека меньше. – Есть ли в этой задаче лишнее данное? (20 пассажиров было в автобусе.) | Решают задачу по дейст- | Фронтальная, индивидуальная | Выполнение задания в тетради | ||
| Задание 11 | • Решите задачу.
Решение: 7 – 5 = 2 (п.). Ответ: на 2 пчелы стало больше. – Выберите верный ответ. – Есть ли в этой задаче лишнее данное? (Нет.) – Сравните эту задачу с задачей № 10 | Решают Находят лишнее данное в условии задачи. Сравнивают задачи | Фронтальная, индивидуальная | Выполнение задания в тетради | ||
| VI. Итоги урока. Рефлексия | Обобщение полученных на уроке сведений | Предлагает оценить свою работу на уроке, заполнив таблицу самооценки. Проводит беседу по вопросам: – Что нового узнали на уроке? – Какие правила чтения математических графов вы знаете? – Как люди научились записывать числа? Каждый оценивает свой вклад в достижение поставленных целей и высказывается одним предложением, выбирая начало фразы из предложенных на рефлексивном экране на доске: • Сегодня я узнал… • Было интересно… • Я приобрел… • Я научился… • У меня получилось… • Я смог… • Я попробую… • Меня удивило… • Урок дал мне для жизни… • Мне захотелось… | Отвечают на вопросы. Проводят самооценку, рефлексию | Индивидуальная, фронтальная | Личностные: понимают, в чем значение знаний для человека, и принимают его. Коммуникативные: выполняют осознанное и произвольное построение речевого высказывания в устной форме. Регулятивные: прогнозируют результаты уровня усвоения изучаемого материала; выделяют и осознают то, что уже усвоено и что ещё нужно усвоить, осознают качество и уровень усвоения | Оценивание работы уча-щихся на уроке |
| Домашнее | Поясняет домашнее задание. № 23 (учебник); № 9 (рабочая тетрадь) | Записывают задание | Фронтальная | Наблюдение |
РЕСУРСНЫЙ МАТЕРИАЛ К УРОКУ
Как люди научились записывать числа
Очень разные и даже забавные были эти «цифры». В Древнем Египте, например, числа первого десятка записывались соответствующим количеством палочек: ч – 1, чч – 2 и т. д. Десять обозначали в виде подковы – ∩. Чтобы записать число 15, нужно было поставить одну подкову и пять палочек: ∩ччччч .
В Индии за две тысячи лет до начала нашего летосчисления появился ноль. Его обозначили так же, как и сейчас. Но ведь мы уже привыкли к нему, а тогда это было великим открытием. Назывался он в то время просто кружком. А в Древней Индии кружок – сунья. Арабы перевели это слово как сифр. Не правда ли, напоминает что-то? Правильно! Цифр – цифра. Так уж получилось, что арабским именем нуля стали называть все остальные знаки. Все они теперь цифры: и 0 – цифра, и 5 – цифра, и 9 – цифра. А само слово ноль возникло позже от латинского nullum – ничто. После того как был создан алфавит, во многих странах числа стали записывать с помощью букв. В Древней Греции и Древней Руси к буквам добавляли еще специальные знаки, чтобы не путать их с обычными буквами.
Немало различных способов записи чисел было создано людьми. В Древней Руси числа обозначали буквами с особым знаком «~» (ти́тло), который писали над буквой.
Первые девять букв алфавита обозначали единицы, следующие девять букв – десятки, а последние девять букв – сотни. Число десять тысяч называли словом «тьма» (и теперь мы говорим: «народу – тьма тьмущая»).
Современная достаточно простая и удобная десятичная система записи чисел была заимствована европейцами у арабов, которые, в свою очередь, переняли ее у индусов. Поэтому цифры, которыми мы сейчас пользуемся, европейцы называют «арабскими», а арабы – «индийскими». Эта система была введена в Европе примерно в 1120 году английским ученым-путешественником Аделардом. К 1600 году она была принята в большинстве стран мира.
Русские названия чисел тесно связаны с десятичной системой счисления. Например, семнадцать означает «семь на десять», семьдесят – «семь десятков», а семьсот – «семь сотен». Однако и эта система оказалась очень громоздкой.
Всем знакома римская нумерация. Чаще всего римские цифры встречаются на циферблате в часах:
| I | II | III | IV | V | VI | VII | VIII | IX | X |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
До сих пор используются римские цифры, которые употреблялись в Древнем Риме уже около 2500 лет тому назад.
I – 1, V – 5, X –10, L – 50, G – 100, D – 500, M – 1000.
Остальные числа записываются этими же цифрами с применением сложения и вычитания. Так, например, число XXVII означает 27, так как 10 + 10 + 5 + 1 + 1 = 27.
Если меньшая по значению цифра (I, X, С) стоит перед большей, то ее значение вычитается.
Например: IV означает 4 (5 – 1 = 4), IX означает 9 (10 – 1 = 9). ХС означает 90. Таким образом, число MCMLXXXIX означает 1989, так как
1000 + (1000 – 100) + 50 + 10 + 10 + 10 + (10 – 1) = 1989.
В настоящее время римские цифры обычно применяются при нумерации глав и разделов книги, месяцев года, для обозначений дат значительных событий, годовщин.
Для вычислений запись чисел с помощью римских цифр неудобна. В этом вы можете убедиться сами, если попробуете выполнить, например, сложение чисел CCXCVII и XLIX или деление числа CCXCVII на число IX.
Большим достижением стало введение нуля, который позволил при записи чисел указывать пропущенный разряд. Способ записи любого числа с использованием всего только десяти цифр 1 2 3 4 5 6 7 8 9 0 был изобретен в Индии. Эта система оказалась настолько простой и удобной, что быстро распространилась по всем странам, а так как распространяли ее именно арабы, а не индусы, то эти цифры мы стали называть арабскими.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
