Урок алгебры в 8 классе "Решение неравенств с одной переменной"

Понятие решения неравенств
с одной переменной

Цели: ввести понятия неравенства с одной переменной и его решения, равносильных неравенств; формировать умение решать неравенства с одной переменной путём перехода к равносильному неравенству.

Ход урока

I. Организационный момент.

II. Проверочная работа.

В а р и а н т 1

1. Используя координатную прямую, найдите пересечение промежутков:

а) (–2; 10) и (0; 15); б) [–3; 6] и [–1; 1]; в) (–∞; 2) и (–2; +∞).

2. Покажите штриховкой на координатной прямой объединение промежутков:

а) [–4; 0] и [–1; 5]; б) (–3; 3) и (–6; 6); в) (–∞; 5) и (–∞; 10).

В а р и а н т 2

1. Используя координатную прямую, найдите пересечение промежутков:

а) [–4; 5] и [0; 10]; б) (–3; –1) и (–2; 4); в) (–∞; 5] и [–5; +∞).

2. Покажите штриховкой на координатной прямой объединение промежутков:

а) (–3; 8) и (1; 9); б) [–4; 4] и [–1; 1]; в) (–∞; 1) и (–∞; 4).

Р е ш е н и е

В а р и а н т 1

1. а) (–2; 10) (0; 15) = (0; 10);

б) [–3; 6] [–1; 1] = [–1; 1];

в) (–∞; 2) (–2; +∞) = (–2; 2).

2. а) [–4; 0] [–1; 5] = [–4; 5];

б) (–3; 3) (–6; 6) =(–6; 6);

в) (–∞; 5) (–∞; 10) =(–∞; 10).

В а р и а н т 2

1. а) [–4; 5] [0; 10] = [0; 5];

б) (–3; –1) (–2; 4) = (–2; –1);

в) (–∞; 5] [–5; +∞) = [–5; 5].

2. а) (–3; 8) (1; 9) = (–3; 9);

б) [–4; 4] [–1; 1] = [–4; 4];

в) (–∞; 1) (–∞; 4) = (–∞; 4).

III. Объяснение нового материала.

1. Неравенство 5х – 11 3 содержит переменную х. При подстановке некоторых числовых значений вместо х мы можем получить как верное, так и неверное числовое неравенство. Н а п р и м е р:

при х = 4 неравенство 5 · 4 – 11 3 – верное (9 3), а

при х = 2 неравенство 5 · 2 – 11 3 – неверное (–1 3). Говорят, что число 4 является решением неравенства или удовлетворяет неравенству.

О п р е д е л е н и е 1: Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.

О п р е д е л е н и е 2: Решить неравенство – значит найти все его решения или доказать, что решений нет.

2. Чтобы решать неравенства, необходимо уметь их преобразовывать к неравенству вида ах b или ax b (где a и b – некоторые числа). Неравенства такого вида называют линейными неравенствами с одной переменной. Данное неравенство должно быть равносильно исходному.

О п р е д е л е н и е 3: Неравенства, имеющие одни и те же решения, называются равносильными.

3. По учебнику на с. 177 разобрать основные свойства, используемые при преобразовании неравенства с одной переменной к равносильному неравенству.

4. Разобрать примеры 1, 2 по учебнику со с. 177–178.

IV. Формирование умений и навыков.

При решении упражнений на этом уроке следует особое внимание уделить правильному использованию свойств при равносильном преобразовании неравенства, а также изображению геометрической модели полученного решения неравенства в виде числового промежутка. На первых порах в ответ можно записывать все три модели, н а п р и м е р:

х ≥ 3; [3; +∞);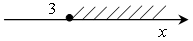

1. № 833, № 834 – устно.

2. № 835.

Р е ш е н и е

а) х + 8 0; х –8;

б) х – 7 х

в) х + 1,5 ≤ 0; х ≤ –1,5;

г) х – 0,4 ≥ 0; х ≥ 0,4;

О т в е т: а) (–8; +∞); б) (–∞; 7); в) (–∞; 1,5]; г) [0,4; +∞).

3. № 837.

Р е ш е н и е

а) 2х х х

б) 5х ≥ –3; х ≥ –3 : 5; х ≥ –0,6;

в) –12х х (–48) : (–12); х 4;

г) –х х (–7,5) : (–1); х 7,5;

д) 30х 40; х 40 : 30; х 1;

е) –15х х (–27) : (–15); х ; х 1,8;

ж) –4х ≥ –1; х ≤ (–1): (–4); х ≤ 0,25;

з) 10х ≤ –24; х ≤ (–24) : 10; х ≤ –2,4;

и) х х ; х х

к) х х 0 : ; х 0;

л) 0,02х ≥ –0,6; х ≥ (–0,6) : 0,02; х ≥ –30;

м) –1,8х ≤ 36; х ≥ 36 : (–1,8); х ≥ –20;

О т в е т: а) (–∞; –8,5); б) [–0,6; +∞); в) (4; +∞); г) (7,5; +∞);

д) ; е) (1,8; +∞); ж) (–∞; 0,25]; з) (–∞; –2,4];

и) (–∞; 12); к) (0; +∞); л) [–30; +∞); м) [–20; +∞).

4. № 838.

5. № 841.

V. Итоги урока.

В о п р о с ы у ч а щ и м с я:

– Что называется решением неравенства с одной переменной?

– Что означает «решить неравенство»?

– Какие неравенства называются равносильными?

– Какие свойства используются для преобразования неравенства в равносильное?

Домашнее задание: № 836, № 839, № 840.