Урок геометрии в 10 классе

УРОК – ИССЛЕДОВАНИЕ ПО ГЕОМЕТРИИ

В 10 КЛАССЕ ПО ТЕМЕ « ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ».

ЦЕЛЬ: Рассмотрение различных случаев построения сечений тетраэдра и параллелепипеда. Формирование у обучающихся навыков построения сечений многогранников.

ХОД УРОКА.

1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ.

Учитель приветствует обучающихся и сообщает им о том, что сегодня они будут работать математиками – исследователями в области построения сечений многогранников. Для этой цели класс делится на две лаборатории: первая будет заниматься рассмотрением сечений тетраэдра, а вторая – рассмотрением сечений параллелепипеда.

2. ВВОДНАЯ БЕСЕДА.

• Что такое многогранник? (Ответ: поверхность геометрических тел, составленная из многоугольников)

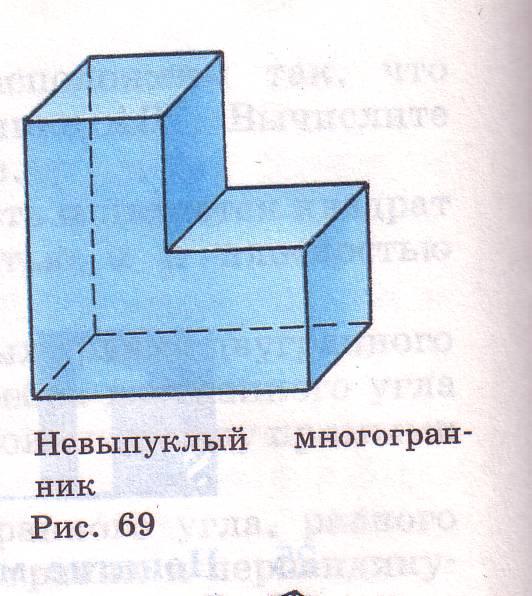
• Какие многогранники называются выпуклыми, а какие – невыпуклыми?

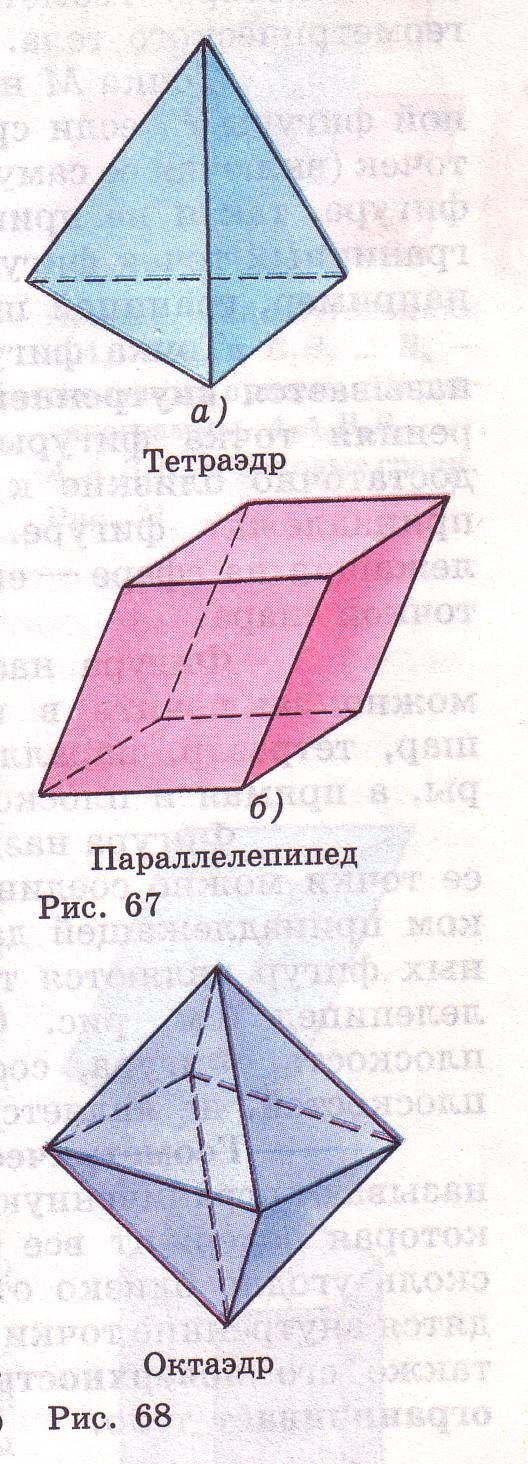
• Какой многогранник называется тетраэдром ? (Ответ: это многогранник, гранями которого являются четыре треугольника)

• Какой многогранник называется параллелепипедом?(Ответ: это многогранник, состоящий из двух равных параллелограммов, расположенных в параллельных плоскостях, и параллельных отрезков, соединяющих соответственные вершины)

• Что мы понимаем под сечением? (Ответ: назовём секущей плоскостью любую плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением).

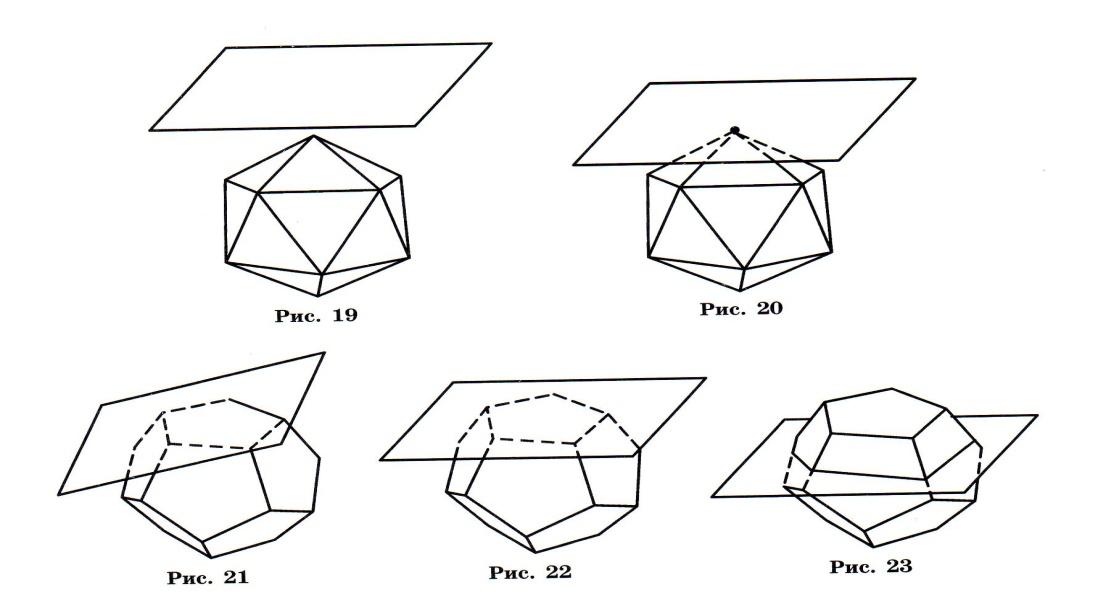
Примеры сечений многогранников: а) нет общих точек (рис.19); б) есть одна общая точка (рис.20); в) есть общий отрезок (рис.21); г) есть общий многоугольник (грань многогранника) (рис.22); д) есть общий многоугольник, не являющийся гранью (рис.23)

• Что понимается под диагональным сечением? (Ответ: сечение многогранника плоскостью, проходящей через диагональ основания и два прилежащих к ней боковых ребра)

3. ГРУППОВАЯ ИССЛЕДОВАТЕЛЬСКАЯ ДЕЯТЕЛЬНОСТЬ.

Ученики рассаживаются по группам и начинают работу по выявлению различных видов сечений тетраэдра и параллелепипеда плоскостями.

ЗАДАЧИ ДЛЯ ПЕРВОЙ ГРУППЫ.

1. На рёбрах АВ, ВД, СД тетраэдра АВСД отмечены точки М, P и N , так что точка М принадлежит ребру АВ, точка Р – ребру ДС, а точка N – ребру ВД. Постройте сечение тетраэдра плоскостью МРN.

2. Точка М лежит на боковой грани АДВ тетраэдра ДАВС. Постройте сечение тетраэдра плоскостью, проходящей через точку М, параллельно основанию АВС.

3. Какой фигурой является сечение правильного тетраэдра АВСД плоскостью, проходящей через вершину В и точки М, Р – середины рёбер соответственно АД и СД?

4. Какие многоугольники можно получить в сечении тетраэдра плоскостью? ( Приведите примеры).

ЗАДАЧИ ДЛЯ ВТОРОЙ ГРУППЫ.

1.На рёбрах параллелепипеда взяты три точки А,В,С. Постройте сечение параллелепипеда плоскостью АВС.

2.Постройте сечение параллелепипеда АВСДА₁В₁С₁Д₁ плоскостью, проходящей через вершины В_{1 ,} Д и точку К – середину ребра СС₁ ?

3. Какой фигурой является сечение параллелепипеда плоскостью, проходящей через две противоположные вершины нижнего основания и середину одного из рёбер верхнего основания?

4. Какие многоугольники можно получить в сечении параллелепипеда плоскостью? (Приведите примеры).

1. ИТОГ УРОКА (В ВИДЕ ЗАЩИТЫ ЗАДАЧИ ПО ТЕМЕ)

Каждой лаборатории предоставляется время для защиты своего научного проекта. В ходе защиты обучающиеся рассказывают о правилах построения сечений тетраэдра и параллелограмма (на классной доске с помощью цветных мелков и чертёжных инструментов). Кроме этого каждая группа рассказывает о выявленных ею видах сечений данных многогранников.

5. ДОМАШНЕЕ ЗАДАНИЕ.

По учебнику «Геометрия 10 - 11» под редакцией Л.С.Атанасяна : пункты 12 – 14 страница 24 – 29, задачи № 75 и № 79 (а), 80, 82 (а), 84. Подготовиться к самостоятельной работе по теме «Построение сечений тетраэдра и параллелепипеда».