Тема урока:
Логарифмическая функция и ее приложение
“ Наука только тогда достигает совершенства,
когда ей удается пользоваться математикой”.
К.Маркс
Цели урока:
ОБРАЗОВАТЕЛЬНАЯ:
Расширить представление учащихся о логарифмической функции, применении ее свойств в нестандартной ситуации.
Формировать навыки умственного труда, нацеливать на поиск рациональных путей решения
Продолжить формировать умение применять основной математический аппарат при постановке и решении задач, возникающих в повседневной практике и непосредственно связанных с процентами.
РАЗВИВАЮЩАЯ:
ВОСПИТЫВАЮЩАЯ:
Сформировать навыки правильного планирования собственной деятельности с учетом биологических ритмов, умение снять напряжение и усталость.
Тип урока: урок систематизации и обобщения полученных знаний с элементами получения новых.
Оборудование урока: мультимедиа-проектор, экран, таймер, доска, карточки-тесты, калькуляторы.
ХОД УРОКА:
Организационный момент
Тест-тренажер. Учащиеся получают тесты, по команде тест переворачивается и учащиеся приступают к работе. (12 минут)
Проверка теста (2 минуты)
Проверка домашнего задания
Любое число – тремя двойками.
Остроумная алгебраическая головоломка, которой развлекались участники одного съезда физиков в Одессе. Задача: любое данное число, целое и положительное изобразить с помощью трех двоек и математических символов. Пусть данное число 3.
Решение:
3= -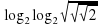 ,
,
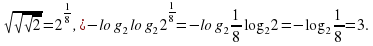
Офтольмопауза (собрать «Змею-рубик)
5. Организация учащихся на работу, постановка цели и задачи.
Мотивация учащихся
Учитель: Сегодня мы постараемся расширить ответ на вопрос
“Зачем в школе изучают логарифмы?”
Мы знаем, что логарифмы появились в XVI в. как средство для упрощения вычислений, но нужны ли они сегодня, когда вычислительная техника достаточно развита, чтобы справляться с самыми сложными расчетами? Ведь не изучаются же в современной школе такие старинные средства для упрощения вычислений, как простейшие счетные приборы, не изучаются древние алгоритмы умножения и деления чисел.
На практике человек всегда интересуется такими вопросами, как, например, насколько быстро растёт та или иная величина, в особенности, если эта величина имеет «экономический» характер – скажем платёж, если его не внести вовремя; сумма денег на его счёте в банке. Если имеется необходимость производить аналогичные одинаковые вычисления для различных исходных сумм и процентных ставок, можно составить формулу или найти её в справочнике и проводить расчёты с помощью вычислений на калькуляторе.
Цели урока для учащихся:
Расширить представление о логарифмической функции, применении ее свойств в нестандартной ситуации
Сформировать умение применять основной математический аппарат при постановке и решении задач, возникающих в повседневной практике и непосредственно связанных с процентами.
6. Установить соответствие между утверждениями, означающими одно и то же:
| Расходы увеличились на 100% | Расходы уменьшились наполовину |
| Расходы увеличились на 50% | Расходы уменьшились вдвое |
| Расходы уменьшились на 50% | Расходы уменьшились примерно в полтора раза |
| Расходы уменьшились на 30% | Расходы уменьшились примерно на треть |
|
| Расходы увеличились наполовину |
|
| Расходы увеличились вдвое |
|
| Расходы увеличились в полтора раза |
|
| Расходы удвоились
|
Задача 1. Подсчитаем, сколько денег получит вкладчик через 5 лет, если 10% будут начисляться на вложенную сумму составляющую 320000 рублей? (учащиеся подсчитывают с помощью калькуляторов)
320000+320000 0,1
0,1 5=480000(руб)
5=480000(руб)
Ответ: 480000 рублей.
Задача 2. Подсчитаем, сколько денег получит вкладчик через 5 лет, если 10% будут начисляться на предыдущую сумму составляющую 320000 рублей? (учащиеся подсчитывают с помощью калькуляторов)
Решение:
320000·1,1= 352000;
352000·1,1=387200;
387200·1,1=425920;
425920·1,1=468512;
468512·1,1=515363,2.
Но так высчитывать суммы очень долго и неудобно, значит можно посчитать следующим образом:
320000·1,15=515363,2.
Вопрос 2. Платежи бывают разные, от чего зависит их размер?
Ответ: Размер платежей зависит ещё и от времени, поэтому появилась необходимость составить общую формулу платежей: Sn=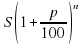 ,
,
где n – число дней.
2. Начальная сумма составляет 2000 рублей. Ежемесячно она увеличивается на 5%. Какая из перечисленных формул соответствует данному условию?
a) S=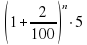 , b) S=
, b) S=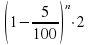 , c) S=
, c) S=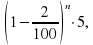 d) S=
d) S= ?
?
Сложный процентный рост:
В сбербанке для некоторых видов вкладов (называемые срочными) принята следующая схема начисления денег на сумму, внесённую в банк. Каждый год она возрастает на некоторое число процентов, если в конце года вкладчик не снял «проценты», то они капитализируются и в конце года проценты начисляются банком уже на новую, увеличенную сумму, то есть начисляются «проценты на проценты».
В математике говорят о сложных процентах и используют следующую формулу: S1=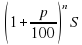 , которая выражает функциональную зависимость вида y = ax
, которая выражает функциональную зависимость вида y = ax
Задача 2. На счёт в банке положили 1 млн. рублей под 30% годовых. Как определить, через какое время сумма на счёте увеличиться в 2 разa?
( С помощью графика y = 1,3x)
Вопрос: А как найти решение без графика функции?
Ответ:
Единственное решение, но оно будет не точным. С помощью логарифма:
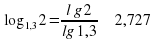 , значит, используя формулу сложных процентов и определение логарифма, можем более точно определить время, за которое происходит увеличение вклада: n=
, значит, используя формулу сложных процентов и определение логарифма, можем более точно определить время, за которое происходит увеличение вклада: n=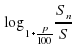 .
.
Задача 3. Сберкасса выплачивает 20 % годовых. Через сколько лет внесенная сумма утроится?
Решение: Пусть первоначальная величина вклада составляет S0 рублей. Тогда через n лет эта величина равняется 2S0 рублей
 ≈
≈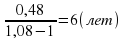 .
.
Ответ: через 6 лет вклад утроится.
Вопрос: В чём разница простого и сложного процентного роста?
Ответ: Разница состоит в том, что при простом росте процент начисляется исходя из начального значения величины, а при сложном он исчисляется из предыдущего значения.
Вопрос: Вкладывая деньги в банк и знакомясь с условиями, какой вопрос вы обязательно должны задать работнику банка, чтобы вложение было выгодным?
Ответ: Какие проценты выплачивает банк – простые или сложные?
7.Физкультминутка
упражнения для снятия утомления.
помогают быстро восстановить силы. выполняем при первых признаках усталости.
1. сложить ладони перед грудью, пальцами вверх, не дышать, сдавить изо всех сил основания ладоней. напряжены мускулы плеч и грудь. втянуть живот ii подняться вверх, как будто, опираясь на руки, выглядываете из окна. всего 10-15 секунд и - стало жарко. - повторить 3 раза.
2.сложить руки в замок, обхватить ими затылок, направить локти вперёд. подтянуть голову к локтям, не сопротивляться, растягивать шейный отдел позвоночника. тянуть ровно - так, чтобы было приятно. 10-15 секунд.
8. Логарифмическая спираль (Презентация, готовят ученики)
9. Домашнее задание. Сборник под редакцией М.И. Сканави.
ГЛ.13. № 219 и № 316-для желающих
ГЛ.9. №268, №283, 284. (комментарий)
10. Логарифмическая «комедия: 2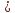 3.»
3.»
«Комедия» начинается с неравенства
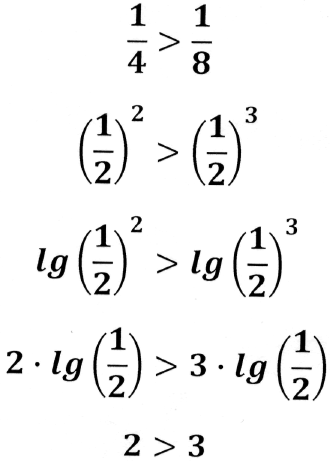
В чем ошибка этого доказательства?
Решение: Ошибка допущена при сокращении на lg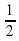 , так как lg
, так как lg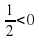 , то при сокращении на lg
, то при сокращении на lg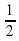 необходимо было изменить знак неравенства, т.е. 2
необходимо было изменить знак неравенства, т.е. 2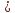 3.
3.
11.Пример. Решить неравенство:
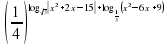
Решение: 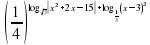
Так как 0
0,
.
Так как 3 1, то 
 .
.
Решаем неравенство
Ответ:
12. Подводятся итоги урока.
Приложение.
Любопытная задача, взятая из книги “Господа Головлевы” Салтыкова-Щедрина:
“Порфирий Владимирович сидит у себя в кабинете, исписывая цифирными выкладками листы бумаги. На этот раз его занимает вопрос: Сколько было бы у него денег, если бы маменька подаренные ему при рождении дедушкой на зубок 100 рублей не присвоила себе, а положила в ломбард на имя малолетнего Порфирия? Выходит, однако, немного: всего 800 рублей?
Предполагая, что Порфирию в момент расчета было 50 лет, и, сделав допущение, что он произвел вычисления правильно (допущения маловероятное, т.к. едва ли Головлев знал логарифмы и умел вычислять сложные проценты), требуется установить, сколько % платил в то время ломбард.
“Завещание на сотни лет”
Известно завещание знаменитого американского государственного деятеля Бенжамина Франклина. Вот извлечение из него.
“Препоручаю тысячу фунтов стерлингов бостонским жителям. Если они примут эту тысячу фунтов, то должны поручить ее отборнейшим гражданам, а они будут в год, в заем молодым ремесленникам. Сумма эта через сто лет возвысится до 131000 фунтов стерлингов. Я желаю, чтобы тогда 100000 фунтов были употреблены на постройку общественных зданий, остальные же 31000 фунтов отданы были в проценты на 100 лет. По истечению второго столетия сумма возрастет до 4060000 фунтов стерлингов. Из коих 1060000 фунтов оставляю в распоряжение бостонских жителей, а 3000000 – правлению Массачустской общины. Далее не осмеливаюсь простирать своих видов”.
Оставляя всего 1000 фунтов, Франклин распределяет миллионы. Математический расчет подтверждает, что соображения завещателя вполне реальны. 1000 фунтов, увеличиваясь в 1,05 раза (т.к. капитал, приносящий 5 %, увеличивается ежегодно в 105 раз), через 100 лет должны превратиться в х = 1000 · 1,05100 фунтов. Это выражение можно вычислить с помощью логарифмов lg 1000 + 100lg1, 05 = 5,11893 откуда х = 131000 в согласии с текстом завещания.
Далее 31000 фунтов в течение следующего столетия превращается в сумму у = 31000 · 1,05100, откуда вычисляя с помощью логарифмов, находим у = 4076000.
Звезды, шум и логарифмы.
Шум и звезды объединяются здесь потому, что громкость шума и яркость звезд оценивается одинаковым образом – по логарифмической шкале.
Астрономы делят звезды по степени яркости на видимые и абсолютные звездные величины – звезды первой величины, второй, третьей и т.д. Последовательность видимых звездных величин, воспринимаемых глазом, представляет собой арифметическую прогрессию. Но физическая по иному закону: яркости звезд составляют геометрическую прогрессию со знаменателем 2,5. Легко понять, что “величина” звезды представляет собой логарифм ее физической яркости. Короче говоря, оценивая яркость звезд, астроном оперирует таблицей логарифмов, составленной при основании 2,5.
Аналогично оценивается и громкость шума. Вредное влияние промышленных шумов на здоровье рабочих и на производительность труда побудило выработать приемы точной числовой оценки громкости шума. Единицей громкости звука служит “бел”, но практически используется единица громкости, равные его десятой доле, - так называемый “децибелы”. Последовательные степени громкости 1 бел, 2 бела, 3 бела, и т.д. Составляют арифметическую прогрессию… Физические же величины, характеризующие шумы (энергия, интенсивность звука и др.), составляют геометрическую прогрессию со знаменателем 10. Громкость, выраженная в белах, равна десятичному логарифму соответствующей физической величины.
Логарифмы и ощущения.
Ощущения, воспринимаемые органами чувств человека, могут вызываться раздражениями, отличающимися друг от друга во много миллионов и даже миллиардов раз. Удары молота о скользкую плиту в сто раз громче, чем тихий шелест листьев, а яркость вольтовой дуги в триллионы раз превосходит яркость какой-нибудь слабо звезды, едва видимой на ночном небе. Но никакие физиологические процессы не позволяют дать такого диапазона ощущений. Опыты показали, что организм как бы “логарифмирует” полученные им раздражения, т.е. величина ощущения приблизительно пропорциональна десятичному логарифму величины раздражения.
Как видим, логарифмы вторгаются и в область психологии.
Не хотелось бы, чтобы Вы пришли к неправильному выводу о том, распределение звезд по звездным величинам обусловлено физическими свойствами самих звезд (яркость, удаленность), а последовательность степеней громкости шума зависит от его характеристик (интенсивность, частота). Все это вытекает из наших ощущений, воспринимаемых органами чувств человека: зрение, слух, осязание, обоняние… Эти ощущения вызываются внешними раздражителями, которые могут отличаться друг от друга. Например, удары молота о скользкую плиту в 100 раз громче шелеста листьев, или яркость вольтовой дуги в триллион раз превосходит яркость звезды еле видимой на ночном небе.
Все закономерности, о которых шла речь выше, являются следствиями общего для всех органов чувств “психофизического закона Вебера-Фехнера”. Фехнер математически выразил тот факт, что ощущение изменяется гораздо медленнее, чем растет сила раздражения.
“Когда величина раздражителя изменяется в геометрической прогрессии, величина ощущения изменяется в прогрессии арифметической”, то есть “Величина ощущения приблизительно пропорциональна логарифму интенсивности раздражителя”.
Таким образом, величина блеска звезд пропорциональна логарифму по основанию 2. 5 его физической яркости, степень громкости шума пропорциональна логарифму по основанию 10 внешнего раздражителя, величина звука пропорциональна логарифму по основанию 2 ее физической характеристики. Числа 2; 2,5; 10 вычислены экспериментальным путем.
Интересный факт: Пример процесса, подчиняемого закону Вебера-Фехнера:
“Продвижение людского потока при эвакуации при пожаре пропорционально логарифму плотности толпы”.
Физики шутят: “ Математика – царица всех наук, но служанка физики”. Так пошутить могут и музыканты, и биологи, и психологи и др. А это еще раз подтверждает правильность слов Карла Маркса “ Наука только тогда достигает совершенства, когда ей удается пользоваться математикой”.
Поистине безграничны приложения показательной и логарифмической функций в самых различных областях науки и техники, а ведь придумывали логарифмы для облегчения вычислений. Более трех столетий прошло с того дня, как в 1614 году были опубликованы первые логарифмические таблицы, составленные Джоном Непером. Они помогали астрономам и инженерам. Сокращая время на вычисления, и тем самым. Как сказал знаменитый французский ученый Лаплас: “Удлиняя жизнь вычислителям”.
Ещё недавно трудно было представить инженера без логарифмической линейки в кармане; изобретенная через десяток лет после появления логарифмов Непера английским математиком Гунтером. Она позволяла быстро получать ответ, с инженерного обихода вытеснила микрокалькулятор, но без логарифмической линейки не были бы построены ни первые компьютеры, ни калькуляторы
Математический тренажер №12
| 1 вариант | 2 вариант |
| 1.Найти значение выражения: |
| | |
| 2.Вычислите значение выражения: |
| | |
| Вычислите: |
| 3. | 3. |
| 4. Если объем куба АВСDA1B1C1D1 равен 1, то объем пирамиды D1АВСD равен… А)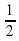 ; Б) ; Б) ; В) ; В)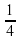 ; Г) ; Г) ; Д) ; Д)  . . | 4. Если объем куба АВСDA1B1C1D1 равен 1, а М1 и М – середины ребер D1C1 u DC соответственно, то объем призмы AMDA1M1D1 равен… А)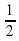 ; Б) ; Б) ; В) ; В)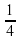 ; Г) ; Г) ; Д) ; Д)  . . |
| 5. Трапеция АВСD вписана в окружность? Угол А равен 60 , угол АВD равен 90 , угол АВD равен 90 , СD = 4см. Найдите радиус окружности. , СD = 4см. Найдите радиус окружности. | 5.В прямоугольной трапеции АВСD меньшая диагональ АС составляет с основанием угол 60 Периметр треугольника АСD равен 36см. Вычислите длину средней линии трапеции, если АС=АD. Периметр треугольника АСD равен 36см. Вычислите длину средней линии трапеции, если АС=АD. |
| 6.Если lo x=4, то x=4, то =… =… 1) ; ; 2) 2)  3)  4) 3; 5) 9. 4) 3; 5) 9. | 6. Если lo x=2, то x=2, то  =… =… 1) ; ; 2) 2)  3)  4) 2; 5) 4. 4) 2; 5) 4.
|
| 7.Решите неравенство |
| | |
| 8. 4-й член арифметической прогрессии равен 9, а 6-й член равен 15. Найти а5 . | 8. . 4-й член геометрической прогрессии равен 9, а 6-й член равен 4. Найти в5 . |
| 9.Две бригады, работая совместно, закончили посадку деревьев за 4 дня. Первая бригада сажала по 20 деревьев, вторая – на 25% меньше. Сколько деревьев было посажено? | 9. Два экскаватора работали на выемке грунта. Первый вынимал в час 30м3 грунта, второй – на 20% меньше. Первый работал 10 часов, второй – 8 часов. Сколько м3 грунта вынули оба экскаватора вместе? |
| 10.Решить уравнение . | 10. Решить уравнение . |
ПРЕЗЕНТАЦИЯ.
Любопытная задача, взятая из книги “Господа Головлевы” Салтыкова-Щедрина:
“Порфирий Владимирович сидит у себя в кабинете, исписывая цифирными выкладками листы бумаги. На этот раз его занимает вопрос: Сколько было бы у него денег, если бы маменька подаренные ему при рождении дедушкой на зубок 100 рублей не присвоила себе, а положила в ломбард на имя малолетнего Порфирия? Выходит, однако, немного: всего 800 рублей?Предполагая, что Порфирию в момент расчета было 50 лет, и, сделав допущение, что он произвел вычисления правильно (допущения маловероятное, т.к. едва ли Головлев знал логарифмы и умел вычислять сложные проценты), требуется установить, сколько % платил в то время ломбард.
“Завещание на сотни лет”
Известно завещание знаменитого американского государственного деятеля Бенжамина Франклина. Вот извлечение из него.
“Препоручаю тысячу фунтов стерлингов бостонским жителям. Если они примут эту тысячу фунтов, то должны поручить ее отборнейшим гражданам, а они будут в год, в заем молодым ремесленникам. Сумма эта через сто лет возвысится до 131000 фунтов стерлингов. Я желаю, чтобы тогда 100000 фунтов были употреблены на постройку общественных зданий, остальные же 31000 фунтов отданы были в проценты на 100 лет. По истечению второго столетия сумма возрастет до 4060000 фунтов стерлингов. Из коих 1060000 фунтов оставляю в распоряжение бостонских жителей, а 3000000 – правлению Массачуйстской общины. Далее не осмеливаюсь простирать своих видов”.
Оставляя всего 1000 фунтов, Франклин распределяет миллионы. Математический расчет подтверждает, что соображения завещателя вполне реальны. 1000 фунтов, увеличиваясь в 1,05 раза (т.к. капитал, приносящий 5 %, увеличивается ежегодно в 105 раз), через 100 лет должны превратиться в х = 1000 · 1,05100 фунтов. Это выражение можно вычислить с помощью логарифмов lg 1000 + 100lg1, 05 = 5,11893 откуда х = 131000 в согласии с текстом завещания.
Далее 31000 фунтов в течение следующего столетия превращается в сумму у = 31000 · 1,05100, откуда вычисляя с помощью логарифмов, находим у = 4076000.






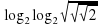 ,
, 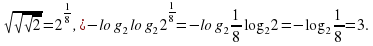
 0,1
0,1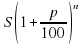 ,
, 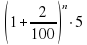 , b) S=
, b) S=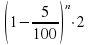 , c) S=
, c) S=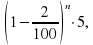 d) S=
d) S= ?
?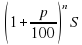 , которая выражает функциональную зависимость вида y = ax
, которая выражает функциональную зависимость вида y = ax 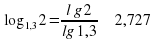 , значит, используя формулу сложных процентов и определение логарифма, можем более точно определить время, за которое происходит увеличение вклада: n=
, значит, используя формулу сложных процентов и определение логарифма, можем более точно определить время, за которое происходит увеличение вклада: n=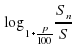 .
.
 ≈
≈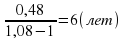 .
.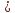 3.»
3.»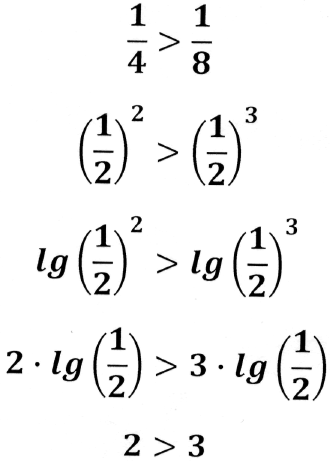
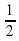 , так как lg
, так как lg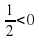 , то при сокращении на lg
, то при сокращении на lg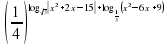
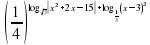
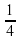 ; Г)
; Г)









