Открытый урок по алгебре
в 8-м классе «Теорема Виета»
Учитель математики
МБОУ «Тюшинская СШ»
Гулова Л.В.
2020
Дата: 21.01.2020
Тема урока: «Теорема Виета».
Тип урока: открытие новых знаний.
Технология: проблемно – диалогическая.
Цель урока: изучить теорему Виета и теорему, обратную теореме Виета.
Задачи урока:
Развивающие:
способствовать развитию умений учащихся обобщать полученные знания, проводить анализ, синтез, сравнения, делать необходимые выводы;
содействовать развитию умений применять полученные знания в типовых и нестандартных условиях; обеспечить условия для развития умений грамотно, четко и точно выражать свои мысли;
создать условия, в которых учащиеся могли бы самостоятельно планировать и анализировать собственные действия, реально оценивать свои возможности и знания, способствовать развитию памяти, внимания.
Воспитательные:
способствовать развитию творческого отношения к учебной деятельности;
обеспечить условия для воспитания положительного интереса к изучению математики;
воспитывать культуру поведения при фронтальной, групповой и индивидуальной работе.
Образовательные:
«открыть зависимость между корнями и коэффициентами приведенного квадратного уравнения»; учить применять теорему Виета и обратную ей теорему для приведенных квадратных уравнений в различных ситуациях;
совершенствовать навык решения квадратных уравнений;
обеспечить мотивацию к учебной деятельности как одно из средств развития и социализации личности учащихся.
Планируемый результат обучения, в том числе и формирование УУД:
Познавательные УУД:
умение структурировать знания, контроль и оценка процесса и результатов деятельности; постановка и формулирование проблемы;
умение осознанно и произвольно строить речевое высказывание;
поиск и выделение необходимой информации; смысловое чтение и выбор чтения в зависимости от цели.
Коммуникативные УУД:
планирование учебного сотрудничества с учителем и со сверстниками, инициативное сотрудничество в поиске и сборе информации;
управление поведением партнера;
умение выражать свои мысли.
Регулятивные УУД:
волевая саморегуляция;
оценка – выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению, прогнозирование; контроль, коррекция;
целеполагание как постановка учебной задачи;
планирование, контроль в форме сличения способа действия и его результата с заданным эталоном;
оценка – оценивание качества и уровня усвоения.
Личностные УУД:
действие смыслообразования.
Основные понятия: приведенное квадратное уравнение, коэффициенты приведенного квадратного уравнения, теорема Виета.
Межпредметные связи: история, литература, биология.
Оборудование: презентация, задания на карточках, эталоны и критерии для проверки и оценки, смайлики для рефлексии, математическое лото, карточки для проведения самостоятельной, частично-поисковой деятельности учащихся.
Ход урока
Организационный момент. Мотивация
- Приветствие учителя.
- Прочитайте высказывание Бернарда Шоу (ирландский драматург, философ и прозаик): «Единственный путь, ведущий к знаниям, - это деятельность» (СЛАЙД)
- Как вы понимаете это высказывание?
-Урок не может быть вне деятельности, мы с вами будем трудиться в поисках научной истины.
Актуализация знаний
- Какую тему мы изучаем последние уроки? (Квадратные уравнения)
Сейчас я предлагаю вам выполнить задание и вспомнить, какие же виды квадратных уравнений вы уже знаете. У каждого на парте есть тест, который называется «Виды квадратных уравнений» подпишите его и на выполнение этого задания у вас ровно минута, время пошло. После выполнения задания ребята делают взаимопроверку по готовому ключу.
Тест «Виды квадратных уравнений» (СЛАЙД)
| Ф.И. | Полное | Неполное | Приведённое | Неприведённое | Общее количество "+" |
| 1. х2 + 8х + 3 = 0 | | | | | |
| 2. 6х2 + 9 = 0 | | | | |
| 3. х2 – 3х = 0 | | | | |
| 4. –х2 + 2х + 4 = 0 | | | | |
| 5. 3х + 6х2 + 7 =0 | | | | |
Ключ к тесту: (СЛАЙД)
| 1. | + | | + | |
| 2. | | + | | + |
| 3. | | + | + | |
| 4. | + | | | + |
| 5. | + | | | + |
Критерий оценивания: (СЛАЙД)
10 "+" оценка - 5.
8, 9 "+" оценка - 4.
5, 6, 7 "+" оценка - 3.
1, 2, 3, 4 "+" оценка - 2.
А сейчас мы с вами разгадаем кроссворд, а в выделенных клетках мы получим тему нашего урока. (СЛАЙД)
Уравнение вида ах2 + bх +с = 0 называется (Квадратным) уравнением.
а – (Первый) коэффициент.
b – (Второй) коэффициент.
с – (Свободный) член.
Квадратное уравнение называется (Приведенным), если его первый коэффициент равен 1.
Величина, определяющая число корней квадратного уравнения, которая вычисляется по формуле D = b2 – 4ac. (Дискриминант)
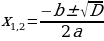 формулы (Корней) квадратных уравнений.
формулы (Корней) квадратных уравнений.
Если D 0, то уравнение имеет (Два) корня.
Если D = 0, то уравнение имеет (Один) корень.
Если D
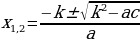 формулы корней квадратных уравнений с (Четным) вторым коэффициентом.
формулы корней квадратных уравнений с (Четным) вторым коэффициентом.
Если в теореме поменять местами условие и заключение, то получится теорема (Обратная) данной.
Запишите, пожалуйста, в тетрадь число, классная работа и тему нашего урока «Теорема Виета». (СЛАЙД)
Создание проблемной ситуации
- А сейчас я предлагаю вам посмотреть ситуацию, которая произошла в семье восьмиклассника.
Сын: Мама, я уже выучил стихотворение, можно мне ехать на тренировку?
Мама: Женя, ты сможешь поехать на тренировку, если за 5 минут найдешь сумму и произведение корней 20 квадратных уравнений.
Сын: Я хорошо решаю уравнения, но за 5 минут мне никак не успеть!!! Папа, мне срочно нужна твоя помощь!!!
Папа: Женя, не переживай. Я открою тебе секрет, и ты справишься с заданием даже быстрей!
Сын: Я все понял, спасибо, папа!
А этот секрет, который папа сказал Жени, вы сами откроете сегодня на нашем уроке.
А вы сможете найти суммы и произведения корней этих уравнений так же быстро? (Нет)
Выдвижение гипотез, формирование целей урока
- Какой у вас возникает вопрос? Что вам предстоит выяснить?
- Сформулируйте цель своей деятельности (Узнать, существует ли связь между корнями и коэффициентами приведенного квадратного уравнения. Если да, то какова эта связь.)
(СЛАЙД) Цели нашего урока:
«открыть зависимость между корнями и коэффициентами приведенного квадратного уравнения»;
научиться применять теорему Виета и обратную ей теорему для приведенных квадратных уравнений в различных ситуациях;
совершенствовать навык решения квадратных уравнений.
Открытие нового знания (СЛАЙД)
- Сейчас мы проведем небольшую исследовательскую работу. Работать будете в группах по 4 человека. Прочитайте задание на карточке. Вы должны заполнить таблицу, проанализировать ее, найти закономерность, и определить связь корней с коэффициентами, сделать вывод.
| 1 группа |
| Уравнение х2 + bх + c=0 | b | c | x1 | x2 | Сумма корней x1 + x2 | Произведение корней x1 · x2 |
| х2 - 10х + 21 = 0 |
|
|
|
|
|
|
| х2 + 7х + 12 = 0 |
|
|
|
|
|
|
| х2 – 3х – 10 = 0 |
|
|
|
|
|
|
| х2 + 3х – 10 = 0 |
|
|
|
|
|
|
| 2 группа |
| Уравнение х2 + bх + c=0 | b | c | x1 | x2 | Сумма корней x1 + x2 | Произведение корней x1 · x2 |
| х2 + 5х + 6 = 0 |
|
|
|
|
|
|
| х2 - 9х + 20 = 0 |
|
|
|
|
|
|
| х2 – 2х – 15 = 0 |
|
|
|
|
|
|
| х2 + 2х – 15 = 0 |
|
|
|
|
|
|
| Выводы по таблице: |
| Все уравнения приведенные, так как a=1 |
| Сумма корней x1 + x2 равна второму коэффициенту с противоположным знаком |
| Произведение корней x1x2 равно свободному члену |
Проверка выполнения заданий в группах, выводы (СЛАЙД)
Общий вывод:
- Утверждение верно для всех уравнений, имеющих корни;
- Это утверждение называется теоремой Виета, названной в честь французского математика Франсуа Виета.
- Послушайте небольшую историческую справку об этом математике. (СЛАЙД)
Франсуа Виет родился в 1540 году во Франции. В родном городке Виет был лучшим адвокатом, но главным делом его жизни была математика. Занимаясь наукой, Виет пришел к выводу, что необходимо усовершенствовать алгебру и тригонометрию. В 1591 году Виет ввел буквенные обозначения и для неизвестных, и для коэффициентов уравнения. Ввел формулы. Франсуа Виет отличался необыкновенной работоспособностью. Иногда, увлекшись каким-нибудь исследованием, он проводил за письменным столом по трое суток подряд.
- Какой же секрет открыл папа Жени? (Теорему Виета)
- Прочитаем теорему в учебнике.
- Запишите теорему в виде формул в тетрадь. (СЛАЙД)
- В этой теореме о каких квадратных уравнениях идет речь? (О приведенных)
-Как быть с неприведенными? (Вначале представить в виде приведенных и применить теорему Виета).
- Для закрепления теоремы Виета я предлагаю вам послушать стихотворение «Теорема Виета». (СЛАЙД)
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого?
Умножишь ты корни – и дробь уж готова.
В числителе c, в знаменателе a
И сумма корней тоже дроби равна.
Хоть с минусом дробь эта, что за беда –
В числителе b, в знаменателе a.
- Существует и теорема, обратная теореме Виета. (СЛАЙД) Прочитайте ее в учебнике, а ее доказательство рассмотрите дома самостоятельно.
(СЛАЙД) Комната психологической разгрузки «Солнечный луч». (Музыка) Детям даётся инструкция: «Сядьте удобнее, закройте глаза. Представьте, что вы лежите на красивой поляне. Сделайте глубокий вдох и медленно делайте выдох, пусть всё напряжение уходит. Вокруг зелёная трава, вдалеке большой лес, поют птицы. Вы чувствуете, какая тёплая земля. Светит яркое солнышко. Один тёплый лучик упал на ваше лицо и пошёл гулять дальше по вашему телу. Вам хорошо и приятно греться на солнышке. Вокруг зелёная трава, вдалеке большой лес, поют птицы. Вы чувствуете, какая тёплая земля. Земля вам даёт силу и уверенность. Сделайте глубокий вдох и медленно делайте выдох, пусть всё напряжение уходит. Ещё раз вдох и выдох... На счёт 5 вы вернётесь обратно. 1 – вы чувствуете, как хорошо лежать и отдыхать. 2, 3, 4 – у вас открываются глаза, 5 – вы возвращаетесь на урок полные сил и уверенности.
Применение новых знаний
Сейчас мы решим номер из учебника. № 581. Один ученик работает у доски, остальные решают самостоятельно в тетрадях. После решения уравнений, вернуться к ситуации с восьмиклассником и еще раз проговорить, какой секрет раскрыл папа сыну.
Загадка
(СЛАЙД) Учитель: Угадайте, о чем говориться. Даю три определения этому предмету:
Главная значимая часть слова, которая выражает основное его значение.
Число, которое после постановки его в уравнение обращает уравнение в верное равенство.
Один из основных органов растений. (Корень)
Рефлексия (СЛАЙД)
Сегодня мы с вами поднялись еще на одну ступеньку, преодолевая квадратные уравнения, сейчас я предлагаю вам определиться на какой ступени оказались вы в конце нашего урока, поднимите смайлик.
Я усвоил тему урока и чувствую себя уверенно
У меня возникли вопросы при изучении теоремы Виета
Я нуждаюсь в помощи
Подведение итогов урока. Оценивание учащихся.
Домашнее задание. (СЛАЙД)
П. 24, № 580, № 582.
И закончить сегодняшний урок хотелось бы словами английского математика XX века У. Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт». Спасибо за урок! (СЛАЙД)
Приложение












Тест “Виды квадратных уравнений”
| Ф.И. | Полное | Неполное | Приведённое | Неприведённое | Общее количество "+" |
| 1. х2 + 8х+3 = 0 | | | | | |
| 2. 6х2 + 9 = 0 | | | | |
| 3. х2 – 3х = 0 | | | | |
| 4. –х2 + 2х +4 = 0 | | | | |
| 5. 3х + 6х2 + 7 =0 | | | | |
Тест “Виды квадратных уравнений”
| Ф.И. | Полное | Неполное | Приведённое | Неприведённое | Общее количество "+" |
| 1. х2 + 8х+3 = 0 | | | | | |
| 2. 6х2 + 9 = 0 | | | | |
| 3. х2 – 3х = 0 | | | | |
| 4. –х2 + 2х +4 = 0 | | | | |
| 5. 3х + 6х2 + 7 =0 | | | | |
Решите уравнения и заполните таблицу.
| 1 группа |
| Уравнение х2 + bх + c=0 | b | c | x1 | x2 | Сумма корней x1 + x2 | Произведение корней x1 · x2 |
| х2 - 10х + 21 = 0 |
|
|
|
|
|
|
| х2 + 7х + 12 = 0 |
|
|
|
|
|
|
| х2 – 3х – 10 = 0 |
|
|
|
|
|
|
| х2 + 3х – 10 = 0 |
|
|
|
|
|
|
Сделайте вывод и заполните таблицу.
| Выводы по таблице: |
| Все уравнения __________________________________, так как а = ____ |
| Сумма корней x1 + x2 равна______________ коэффициенту _________________________________ |
| Произведение корней x1 · x2 равно _______________________________________________________ |
Решите уравнения и заполните таблицу.
| 2 группа |
| Уравнение х2 + bх + c=0 | b | c | x1 | x2 | Сумма корней x1 + x2 | Произведение корней x1 · x2 |
| х2 + 5х + 6 = 0 |
|
|
|
|
|
|
| х2 - 9х + 20 = 0 |
|
|
|
|
|
|
| х2 – 2х – 15 = 0 |
|
|
|
|
|
|
| х2 + 2х – 15 = 0 |
|
|
|
|
|
|
Сделайте вывод и заполните таблицу.
| Выводы по таблице: |
| Все уравнения __________________________________, так как а = _____ |
| Сумма корней x1 + x2 равна______________ коэффициенту _________________________________ |
| Произведение корней x1 · x2 равно _______________________________________________________ |







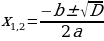 формулы (Корней) квадратных уравнений.
формулы (Корней) квадратных уравнений.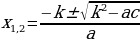 формулы корней квадратных уравнений с (Четным) вторым коэффициентом.
формулы корней квадратных уравнений с (Четным) вторым коэффициентом.












