Урок по теме: "Числовая окружности" 10 класс

Тема урока : Числовая окружность.

Цель урока:

- ввести понятия числовой окружности и единичной окружности; научить учащихся находить на числовой окружности точки, соответствующие заданным числам, выраженным в долях числа π.

- способствовать развитию пространственного воображения, умению работать с интерактивной доской, развитие логического мышления, вычислительных навыков, памяти, внимания.

- содействовать воспитанию интереса к математике, активности, мобильности.

Тип урока: изучение нового материала с применением информационных технологий.

Методы обучения: объяснительно — иллюстративный, использование слайдов при объяснении нового материала.

Оборудование: интерактивная доска с проектором, шаблоны — макеты окружностей.

Ход урока:

1. Организационный момент.

- приветствие;

- проверка готовности класса к уроку.

2. Актуализация знаний учащихся.

С понятием функция вы знакомы с 7 класса, сегодня мы начинаем изучать большой раздел в математике, в котором продолжим изучение функций, их свойств и для начала повторим, что нам о них известно.

Устная работа: Слайд 1

— Какая из предложенных формул задаёт изображённую на графике функцию?

— Перечислите свойства изображённых функций.

Слайд 2

— Дайте характеристику каждой прямой

— Составьте ее уравнение

Слайд 3

— Как называется данный вид функций?

— Перечислите свойства этой функции.

— Какие функции называются числовыми? (Числовой функцией с областью определения X называется соответствие, при котором каждому значению независимого аргумента x ставится в соответствие по некоторому правилу f определённое число y. В аналитической записи этих функций используют алгебраические операции над переменными.)

Математические модели некоторых реальных ситуаций часто бывают связаны с функциями другого типа. Мы начинаем знакомство с первыми представителями класса неалгебраических функций — тригонометрическими функциями. Для этого нам потребуется новая математическая модель.

Слайд 4

— Что вы видите на слайде? (Окружность).

— Что называется окружностью?

— Как найти длину окружности? (L=2πR).

3. Объяснение новой темы.

Новой математической моделью является числовая окружность. Каждому ученику раздается лист с макетом окружности, с использованием которой будет изучаться новый материал.

Слайд 5

1)Любую окружность можно рассматривать как числовую, но удобнее всего использовать единичную окружность — окружность с радиусом 1.

На макете ученики отмечают длину половины

окружности и длину четверти окружности,

отмечают четверти. На этом этапе необходимо

акцентировать внимание учащихся на

положительное и отрицательное направление

обхода окружности.

Слайд 6

2)Мы обошли полностью круг по окружности

от 0 до 2π и можем продолжить движение,

пройдя от 2π четверть окружности, попадём в

точку, которую уже отметили, но соответствовать

она будет уже другому числу: и т.д. Для числовой окружности справедливо следующее утверждение: если точка М числовой окружности соответствует числу t, то она соответствует и числу вида t + 2πk, где параметр k – любое целое число.

Слайд 7 1)Каждую из четырех четвертей числовой

окружности делим на две равные части, и около

каждой точки записываем «имя» при

положительном направлении обхода окружности.

2)Каждую из четырех четвертей числовой

окружности делим на три равные части.

Слайд 8 Выполнить работу можно в интерактивном режиме.

Слайд 9

Во всех разобранных примерах точки и длины дуг на единичной окружности соответствовали долям числа π, но мы можем найти такие точки, которые будут соответствовать числам 1, 2. 3, 4…. .

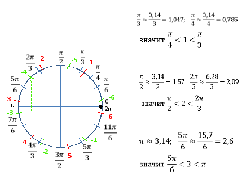
4. Закрепление изученного материала.

Решить на интерактивной доске и в тетрадях:

№ 11.6 — № 11.9 (в, г) № 11.15 — 11.17 (в, г).

5. Итоги урока.

Вместе с учащимися на макете на интерактивной доске отметить «имена» точек при положительном направлении обхода окружности.

6. Домашнее задание.

Изучить по учебнику на стр. 86–91 теоретический материал и решение примеров 1 — 3; решить № 11.6 — № 11.9 (а, б), № 11.15 — 11.17 (а, б).

Литература:

1. Учебник для общеобразовательных учреждений (профильный уровень). Алгебра и начала анализа. 10 класс под редакцией А. Г. Мордковича. Издательство «Мнемозина», Москва 2007.

2. Задачник для общеобразовательных учреждений (профильный уровень). Алгебра и начала анализа. 10 класс