Урок по теме: «Решение тригонометрических уравнений»
Тип урока: урок повторения и обобщения знаний, закрепления умений.
Цели и задачи урока:
1) образовательные – сформировать у учащихся умение различать тригонометрические уравнения по способам решения, отработать навыки решения всех видов тригонометрических уравнений;
2) развивающие – развивать умения работать с книгой, самостоятельно добывать знания; развивать и совершенствовать умения применять имеющиеся у учащихся знания в изменённой ситуации; развивать логическое мышление, умение делать выводы и обобщение;
3) воспитательные – воспитывать трудолюбие, умение общаться со своими сверстниками в процессе работы в парах, аккуратность, культуру поведения, чувство ответственности.
Оборудование урока: презентация, магнит, карточки; чистые листы для самостоятельной работы; таблицы по тригонометрии:
а) значения тригонометрических функций;
б) решение простых тригонометрических уравнений (частные случаи);
в) основные формулы тригонометрии;
Литература:
А. Н. Колмогоров Алгебра и начала анализа, 10-11.
М.И. Башмаков Алгебра и начала анализа: Учебник для 10-11 кл сред. шк..
А.Г.Мордкович Математика : Учебник для 10 кл.
Структура урока:
Ход урока:
Задача: подготовить учащихся к работе на уроке. Взаимное приветствие; проверка подготовленности учащихся к уроку, организация внимания.
Великий физик, математик и политик А. Эйнштейн заметил: «Мне приходиться делить время между политикой и уравнениями. Однако, уравнения гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно». Сегодня на уроке мы повторяем, приводим в систему наши знания по решению тригонометрических уравнений. И ваша задача – показать свои знания и умения по их решению.
Пояснить учащимся, что в процессе работы над учебными элементами учащиеся они уметь:
1 уровень – решать простейшие тригонометрические уравнения; решать тригонометрические уравнения по заданному алгоритму.
2 уровень – решать тригонометрические уравнения, самостоятельно выбирая метод решения.
3 уровень – применять полученные знания в нестандартных ситуациях.
1 уровень – самый общий, т.е. знаниями этого уровня должны овладеть все учащиеся.
2 уровень включает все, что достигнуто на 1 уровне, но в более сложном виде.
3 уровень – все, что достигнуто на 1 и 2 уровнях, но теперь должно применяться в нестандартных ситуациях.
Тригонометрия традиционно популярна при проведении всевозможных экзаменов (в том числе ЕГЭ), конкурсов, олимпиад. В связи с этим очень важно научиться решать тригонометрические уравнения, определять способы решения тригонометрических уравнений.
Устно:
Что называется arcsin а?
Что называется arccos а?
Чему равен arcsin (-а)?
Чему равен arccos (-а)?
Назовите формулу нахождения корней уравнения вида sin x = a.
Назовите формулу нахождения корней уравнения вида cos x = a.
Вычислите:
arcsin  ; 2) arccos
; 2) arccos  ; 3) arctg
; 3) arctg 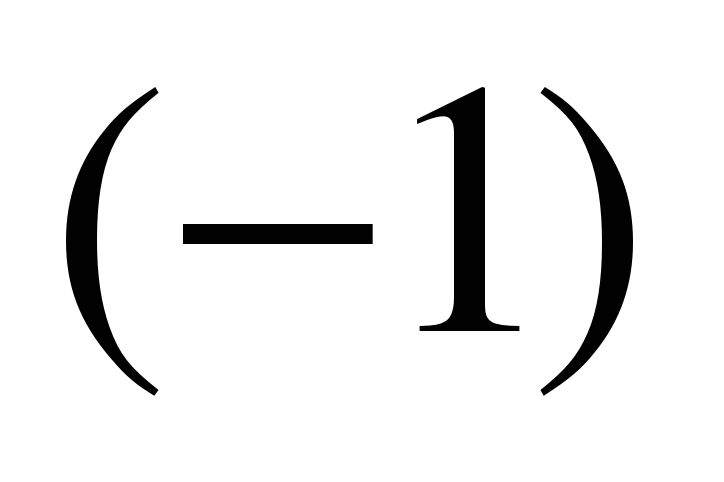 ; 4) arcsin
; 4) arcsin 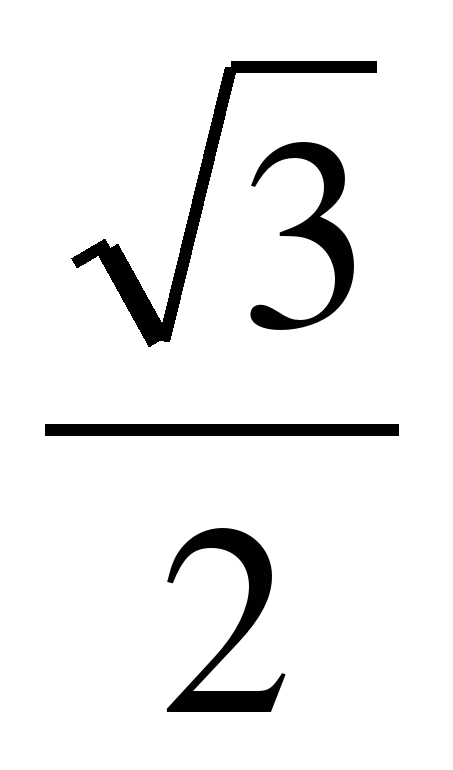 .
.
Решите уравнения
1) sin x = 1,5; 2) cos x = -2.
4.Найти ошибки в решениях тригонометрических уравнений:
(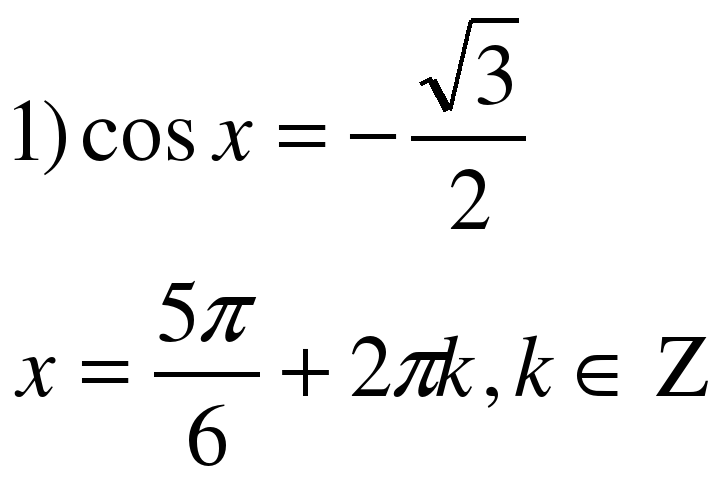
 ±)
±)  (-1k)
(-1k) 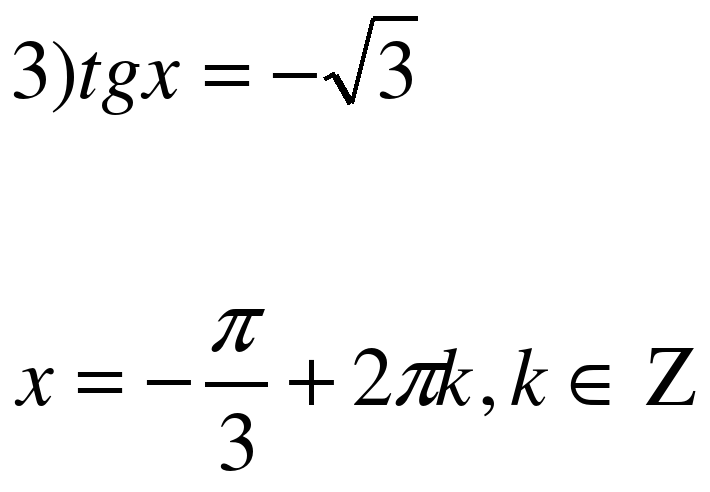 (πk)
(πk)
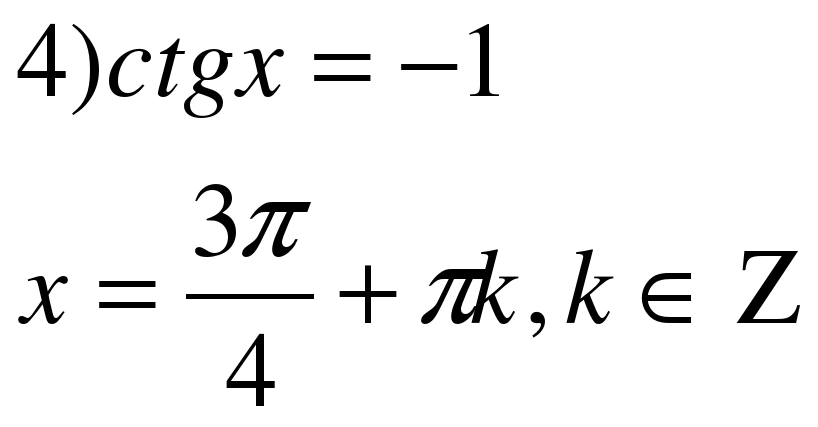 (верно)
(верно) 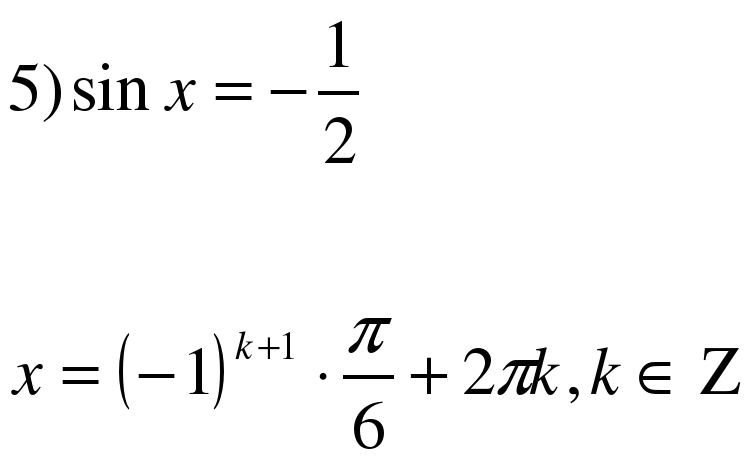 (πk)
(πk)
sin x = 0, Х= (верно)
4.Каким способом можно решить уравнения.
1.cos (4x – 2) = 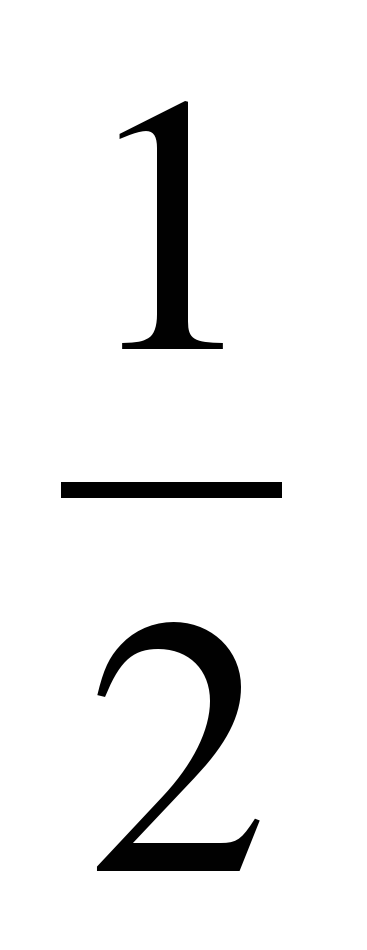 ; 2. cos2 x – 2cos x = 0;
; 2. cos2 x – 2cos x = 0;
3. cos2 x – sin2 x = 1; 4. sinx +sin3x = sin5x – sinx;
5. 3sin2 x – 5sin x – 2 = 2; 6. 2sin x – 3cos x = 0;
7. (tg x - 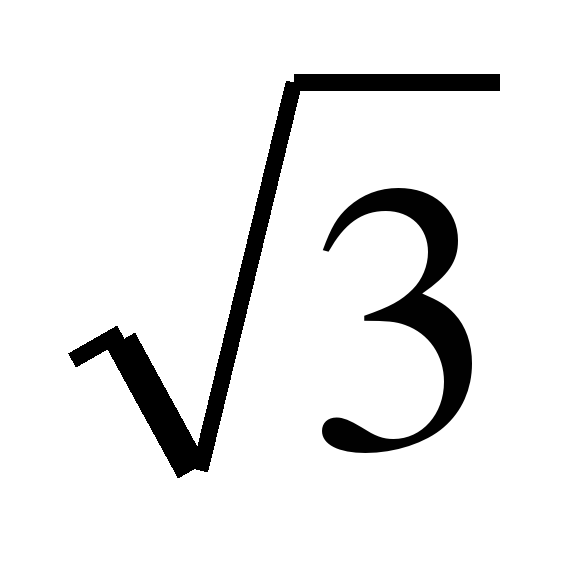 )(2sin
)(2sin  + 1) = 0; 8. 3sin2 x – 4sin x cos x + cos2 x = 0;
+ 1) = 0; 8. 3sin2 x – 4sin x cos x + cos2 x = 0;
9.  ; 10. cos x + cos 2x + cos 3x = 0
; 10. cos x + cos 2x + cos 3x = 0
Цель: закрепить умения решать тригонометрические уравнения методом сведения к квадратному.
Метод сведения к квадратному уравнению состоит в том, что, пользуясь изученными формулами, надо преобразовать уравнение к такому виду, чтобы какую-то функцию (например, sin x или cos x ) или комбинацию функций обозначить через у, получив при этом квадратное уравнение относительно у.
Пример. Решить уравнение 4 -  .
.
Решение: Вместо  подставим тождественное ему выражение
подставим тождественное ему выражение  Тогда исходное уравнение примет вид
Тогда исходное уравнение примет вид

Если ввести y = sin x , получим квадратное уравнение
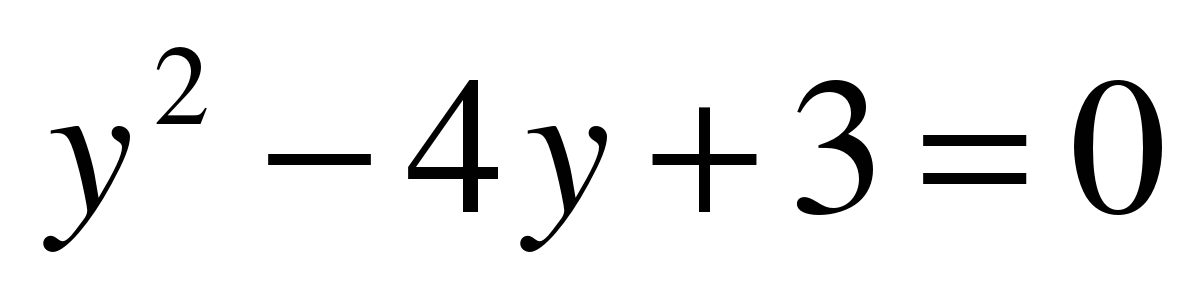
Оно имеет корни 1 и 3. Значит, исходное уравнение равносильно совокупности уравнений
sin x = 1 или sin x = 3.
Уравнение sin x = 1 имеет решение x = 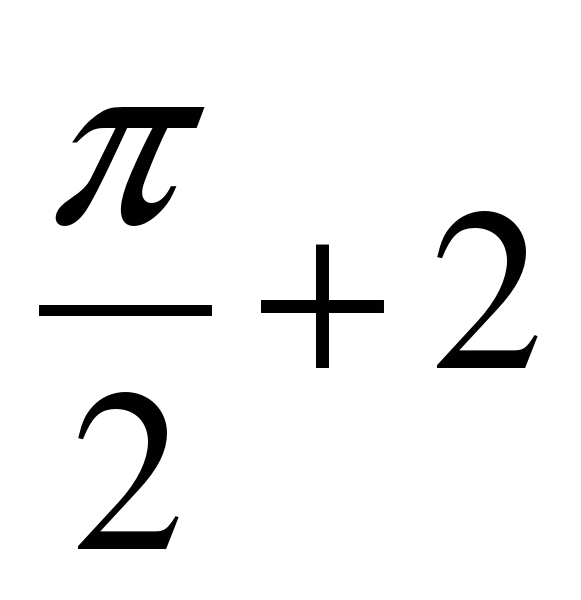
 n, n
n, n .
.
Уравнение sin x = 3 решений не имеет.
Ответ: 
| 1 вариант | 2 вариант |
|  (2 б) (2 б)
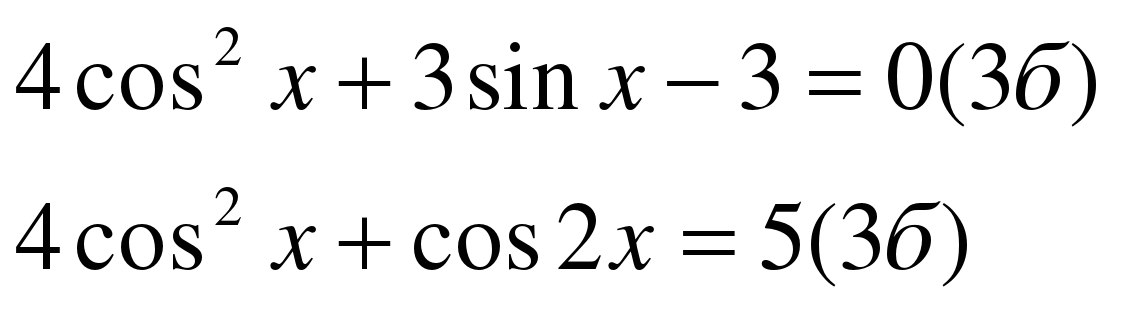
| |
|
|
|
Цель: закрепить навык решения однородных уравнений.
Покажем как решать однородное уравнение 1-й степени, т.е.
Пример 1. Решить уравнение .
Поделим обе части уравнения на cos x или sin x. Но предварительно надо доказать, что это выражение никогда не обращается в нуль. Предположим, что cos x=0. Тогда 5sin x-2∙0=0 sin x=0. Получается, что если sin x=0, то и cos x=0 , чего быть не может ввиду равенства .
Значит можно поделить уравнение на cos x:
Получим уравнение 5tg x-2=0. Отсюда .
Решение однородных уравнений вида начинается с того, что обе части уравнения делят на .
Пример 2. .
Решение. Данное уравнение не является однородным. Но его можно превратить в однородное, заменив 3sin2x на 6sin x cos x и число 2 на .
Приведя подобные слагаемые, получим уравнение
. Аналогично решению примера 1, докажем, что cos x0 .
Тогда можно обе части уравнения поделить на  . Получим
. Получим
или . Отсюда
.
Самостоятельная работа.
| 1 вариант | 2 вариант |
| 8 (2 балла) | (2 балла) |
| 3 (3 балла) | (3 балла) |
Физкультминутка. Примите удобную позу сидя на стуле. В положении сидя, ноги согнуты в коленях под углом приблизительно 100 градусов. Согните стопу, опираясь на пятку и приведя к голени, свободно отпустите. Вместе и попеременно.
Вы освоили решение уравнений 2 уровня сложности. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных ситуациях.
Самостоятельная работа.
(задания не ограничиваются временными рамками, так как их решают далеко не все учащиеся )
sin6x+cos6x=1-2sin3x (2 )
cos2x = (cos x – sin x)
1 – sin2x = cos x – sin x
-
-
-
sin x(sin x+cos x)=1
-
Каждое задание - 2 балла
Проверьте и оцените свои работы. Исправьте ошибки, если они есть, подсчитайте количество баллов. Проставьте количество баллов в оценочный лист. Оцените свои работы.
Дифференцированная домашняя работа.
На “3”. Решите уравнения:
1) sinx=1/2
2) cos2x-9cosx+8=0
3) 3cosxsinx-sinx=0
На “4”. Решите уравнение:
1) cos2x-9cosx+8=0
2) 3cosx+sinx=0
3) 3sin2x+sinxcosx- 2cos2x=0
На “ 5”. Решите уравнение:
1) 2cos2x+3sinx=0
2) 3sinxcosx-cos2x=0
3) 2sin2x-3sinxcosx+4cos2x=4
Подведение итогов. Выставление оценок.
Оценка за весь модуль зависит от суммы баллов по всем учебным элементам. Если сумма больше 31, то вы получаете «5», при получении от 25 до 30 баллов – оценка «4», при получении от 21 до 24 баллов – оценка «3», менее 20 балла вы получаете «2». Для тех, кто получил неудовлетворительную оценку проводится коррекционная контрольная работа.
Рефлексия.
1.Прочитайте ещё раз требования к уровню подготовки и ответьте на вопрос:
- Достигли ли Вы цели урока? В какой степени?
2. Вопрос классу: «Оцените своё самочувствие на уроке, поставив какой-либо значок на графике функции у = sin х, изображенной на доске. Где вы себя ощущали: на гребне волны синусоиды или во впадине?
Хочется закончить урок словами Я.А.Коменского: “ Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию ”.
Приложение 1. Оценочный лист учащегося.
| Фамилия |
| Имя |
| УЭ | К-во баллов за основные задания | Корректирующие задания | Общее к-во баллов за этап |
| № 1 |
|
|
|
| № 2 |
|
|
|
| № 3 |
|
|
|
| № 4 |
|
|
|
| № 6 |
|
|
|
| Итоговое количество баллов |
| Оценка |
Министерство образования и науки РФ
ФГБОУ ВПО " Тувинский Государственный Университет"
Физико-математический факультет
кафедра математического анализа и МПМ
Разработка урока по математике
на тему
" Решение тригонометрических уравнений".
Выполнила: студентка ТувГУ ФМФ
5 курса 1 группы по специалности
"математика с доп. спец.информатика"
Хомушку Чодураа Мергеновна
Проверила: к.п.н., доцент кафедпы
мат.анализа и МПМ
Кара-Сал Надежда Маасовна.
Кызыл - 2015 г.







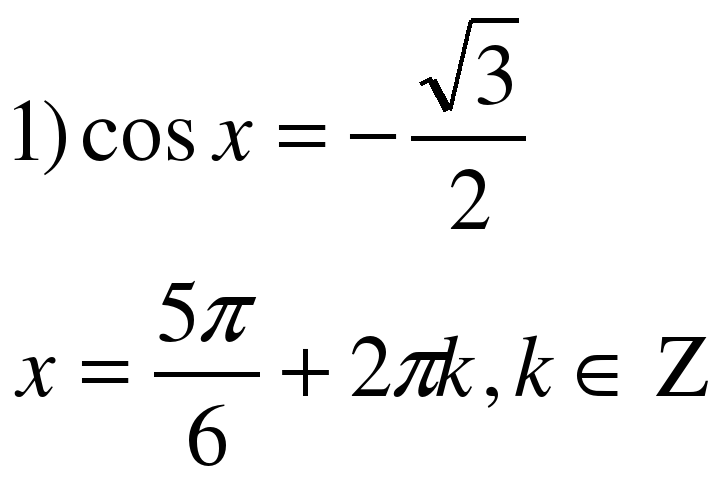
 (-1k)
(-1k) 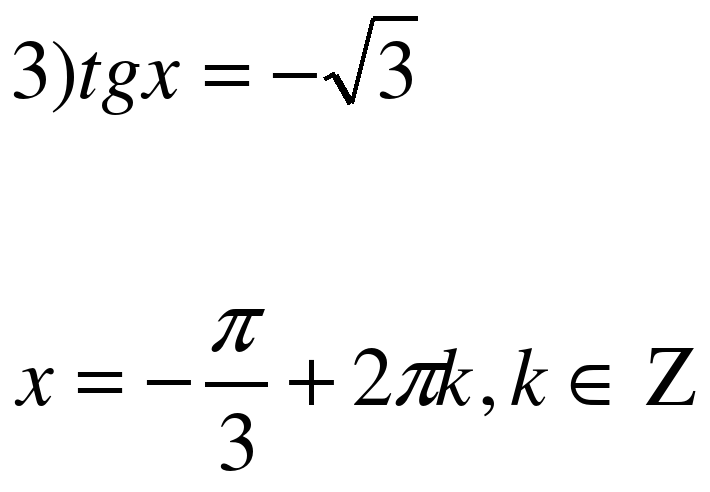 (πk)
(πk)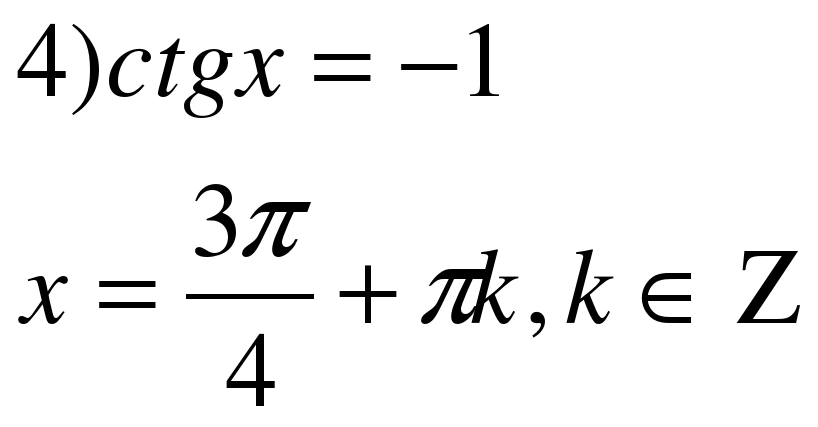 (верно)
(верно) 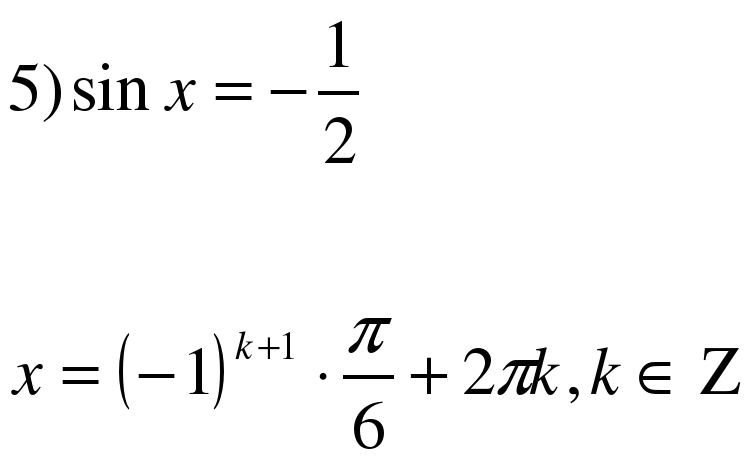 (πk)
(πk)










