Открытый урок по алгебре в 8 классе
Тема: «Решение линейных неравенств с одной переменной»
Девиз урока: Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.
Цель урока: систематизация знаний по решению неравенств.
Задачи:
1) Образовательная: Развитие умения применять свойства числовых неравенств при решении неравенств с одной переменной (в ходе рассмотрения алгоритма решения). Развитие мышления учащихся (в ходе выполнения заданий актуализации и на протяжении всего урока). Развитие внимания учащихся (выполнение заданий на нахождение соответствия, решение неравенств по алгоритму). Развитие памяти учащихся(выполнение заданий в тестовой форме). Развитие вычислительных навыков (выполнение заданий по алгоритму решения неравенств с одной переменной).
2) Развивающая: Развивать навыки коллективной работы, взаимопомощи, самоконтроля.
3)Воспитательная: Воспитать информационные компетенции, математическую зоркость, математическую речь.
Тип урока: Урок систематизации и обобщения изученного материала.
Вид урока: Комбинированный урок
Методы: по характеру познавательной деятельности.
1.Частично-поисковый (при рассмотрении применения свойств для решения неравенств с одной переменной).
2.Репродуктивный (при решении неравенств по алгоритму).
3.Работа по тестовым технологиям (актуализация, контроль знаний).
Оборудование:
1. Компьютер, проектор, экран, доска.
2. Подготовленная презентация.
Структурные элементы урока:
1) Организационный этап.
2)Этап подготовки учащихся к активному сознательному усвоению знаний, постановка целей и задач урока.
3)Этап повторения, систематизации изученного материала, обобщение.
4)Самостоятельная работа (тестирование) по вариантам с взаимопроверкой.
5)Подведение итогов урока. Задание на дом.
Ход урока:
Организационный этап. Слайд 2-3.
Этап подготовки учащихся к активному сознательному усвоению знаний, постановка целей и задач урока. Слайд 4–8.
Мы изучаем тему: «Решение неравенств с одной переменной». Для повторения теории темы, её понимания проведём тестирование. Учащимся предлагается текст. Они отмечают знаком («+») то, что им известно, («-») то, что не знакомо или не понятно. Слайд 9-11.
По результатам текста учитель задает дополнительные вопросы по теории.
3) Этап обобщения и систематизации знаний.
А)Повторение изученного:
1)Учащимся на внимание предлагается соотнести неравенства с числовым промежутком и наоборот. Слайд 12-13.
2)Для повторения темы, её понимания и умения применять знания проводится тестирование с последующей проверкой. Каждое задание теста предлагает ответы «Да» или «Нет».
«Да» - 1; «Нет» - 0.
В результате выполнения теста получается какое-то число. Слайд 15(вопросы теста).
1)Является ли число 14 решением неравенства 2х 10?
2) Является ли число - 5 решением неравенства 4х 12?
3)Является ли неравенство 5х – 15 4х + 14 строгим?
4)Существует ли целое число принадлежащее промежутку [- 2,8;- 3,6]?
5)При любом ли значении переменной а верно неравенство а² + 9 0?
6)Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число знак неравенства не меняется?
- Назовите число, которое у вас получилось.
-Давайте проверим ответ. 101110 – Слайд 16.
3)Устная работа:
- Проведите экспертизу, найдя ошибку. Слайд 17.
Х ≥ 7 2) У 2,5


2,5
Ответ: (-∞;7) Ответ: (-∞;2,5]
3) m ≥ 12 4) x ≤ -1,3


 - 1,3
- 1,3
Ответ: (-∞;12) Ответ: [-∞;-1,3]
- Чтобы приступить к решению неравенств с одной переменной повторим алгоритм решения. Слайд 18.
Учащимся на примере решения неравенства называют алгоритм решения комментируя каждое из преобразований.
Пример: решить неравенство 5(х – 3) 2х - 3
5х – 15 2х - 3
Раскрываем скобки.
5х–2х-3+15
Переносим слагаемое с Х в левую часть, числа в правую, меняя при переносе знак на противоположный.
3х 12
Приводим подобные слагаемые.
х 4
Делим на число при Х, учитывая знак этого числа.
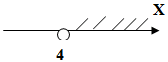
Переходим от аналитической модели к геометрической.
Ответ: (4; +∞)
Пишем ответ в виде числового промежутка.
Работа у доски. Слайд – 19.
Учащимся по карточкам выдается задание: решить неравенство и изобразить множество его решений на координатной прямой.
Задания составлены с учетом индивидуальных способностей учеников и имеют разноуровневый характер.
1-й уровень: 2-й уровень: 3-й уровень:
х – 7 3 30 + 5 х x-1)(3x+1)x+2)²
х + 2 14 + 2 х
4 х - 8
Релаксационная пауза.
- Учащимся предлагается проверить ответы. Слайд – 20.
1)Закрепление навыков решения продолжается.
Учащимся дается задание по вариантам: Слайд – 21.
Решите неравенства
1) 6-2xx
2) 2(3x-7)x-11
И укажите наибольшее целое число, которое является его решением.
2)Проверка решения. Слайд – 22.
3)Закрепление изученной темы: Слайд – 23,24.
Найди ошибку в решении неравенств. Объясни, почему допущена ошибка.
Запиши в тетради правильное решение.
1) 3(2x+1)-12x -3x 2) 3(7-2y) y-7
6x+3-12x -3x 21 -6y y-7
-6x+3x -3 -6y -y -7-21
-3x -3 -7y - 28
х 1 y
Ответ:(1;+∞) ответ: (4 ;+ ∞)
3) .-5(x-1)+5 ≤ -3(x+2) 4) 5-3y ≤ 80
-5x+5+5 ≤ -3x-6 -3y ≤ 75
-5x-3x ≤ -6-10 y ≥ -25
-8x ≤ -16 ответ: (-∞;-25)
x ≥ 2
ответ: [2;+∞)
- Самостоятельная работа(тестирование) по вариантам с взаимопроверкой. Слайд – 25.
- Проверка самостоятельной работы. Слайд – 27.
- Подведение итогов, оценка знаний по теме учениками. Слайд – 28.
Домашнее задание. Слайд – 29. № 853; №856; №857(в,г)


















