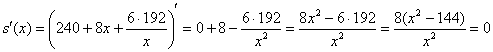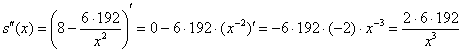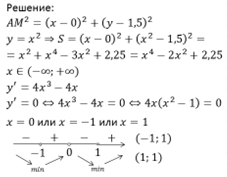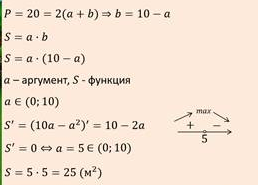Конспект урока по алгебре в 10 классе на тему
«Решение задач на оптимизацию с помощью производной»
Тип урока: Изучение нового материала.
Форма урока: Урок открытия нового знания.
Технология: педагогическая мастерская «Задачи Дидоны».
Продолжительность: 45 минут.
Цель урока: познакомиться с алгоритмом решения задач на оптимизацию с помощью производной.
Методы: словесные, наглядные, практические.
Формы обучения: работа в группах, индивидуальная.
Задачи урока:
Образовательные: научиться решать задачи на оптимизацию с помощью производной.
Развивающие: способствовать развитию внимания, памяти, умственной деятельности и познавательного интереса учащихся, коммуникабельности, математической речи, умения оценивать себя, умение работать в группах; развитие способностей математической деятельности, необходимой для продуктивной жизни в обществе.
Воспитательные: воспитание интереса к предмету через игровые моменты урока, уверенности в собственных силах, целеустремлённости, толерантности.
Планируемые результаты:
Личностные:
- проявляют положительное отношение к урокам математики, овладеть умением правильно и корректно выражать собственное мнение; овладеть умением учиться самостоятельно; овладеть умением выражать свои мысли в письменной форме; научиться применять полученные знания и умения к решению новых проблем.
Метапредметные:
- сформировать умение устанавливать причинно-следственные связи, оценивать правильность выполнения учебной задачи, собственные возможности её решения.
Предметные:
- решают задачи на оптимизацию с помощью производной по заданному алгоритму.
Оборудование: компьютер, мультимедийный проектор, презентация «Мастерская Задачи Дидоны», выполненная с помощью программы Microsoft Power Point, сигнальные карточки красного и зеленого цвета, карточки зеленые и желтые с заданиями, учебник «Алгебра 10-11 класс», Колмогоров А.Н.
План урока:
Индуктор (5 мин)
Деконструкция (4 мин)
Реконструкция (3 мин)
Социоконструкция (7 мин)
Социализация (15 мин)
Афиширование (9 мин)
Рефлексия (2 мин)
| Этап урока | Содержание этапа |
| Индуктор Создание мотивационной базы для активной работы ученика. Создание эмоционального настроя, включение подсознания, создание личного отношения к предмету обсуждения. | Учитель хаотически выкладывает на парты учащихся карточки различных цветов. Учащимся с одинаковым цветом карточки необходимо соединиться в одну группу. В одной группе максимум 5 учеников. Учитель выдает каждой группе набор карточек с заданиями, которые пронумерованы в том порядке, в котором понадобятся на уроке. Работа с карточкой №1. Задание ― разгадать кроссворд, определить выделенное слово. Работа с карточкой №2. Работа с текстом. В группе ответить на вопросы. Коллективное обсуждение ответов с учителем. |
| Деконструкция Разрушение, хаос, неспособность выполнить задание имеющимися средствами. Формирование информационного поля. | Работа с карточкой №3. Работа с задачей «Много ли человеку земли надо?» по рассказу Л.Н. Толстого. Обсуждение описанной ситуации в группах. (1, 2 вопрос).
Ответы на вопросы: S=78 км2 Да, мог. Если четырехугольник был бы прямоугольником. |
| Реконструкция предполагает переход от чувств, эмоций к реальным действиям, оформление ощущений в виде гипотезы, текста, рисунка, проекта. | Работа с карточкой №3. Ответить на 3-4 вопрос.
Ответы на вопросы: 3.Пусть х-длина прямоугольника, тогда 20-х ― ширина. S(x)=20x-x2 4. Минимальное или максимальное значение можно находить либо используя свойства функции, либо с помощью производной. |
| Социоконструкция Объединение гипотез, взаимная оценка индивидуально созданных проектов позволяют ученику сопоставить свои знания с опытом товарища, скорректировать их с учетом полученной в процессе взаимодействия информации, таким образом, происходит взаимообогащение субъективного опыта партнеров. | Работа с карточкой №3. Ответить на 5 и 6 вопрос. Коллективное обсуждение ответов на 3-5 вопрос с учителем.
Ответы на вопросы: 5. Более универсальным методом является нахождение минимального или максимального значения с помощью производной, так как функции могут быть довольно трудными. S’(x)=20-2x 20-2x=0 x=10 – длина 20-х=20-10=10 – ширина Искомый прямоугольник ― квадрат со стороной 10 км. Алгоритм: Составление математической модели. Работа с составленной моделью. Ответ на вопрос задачи. |
| Социализация Групповая работа обеспечивает интеграцию идей, вариантов, вопросов, проблем, оформление общего проекта, разработку модели, совместную корректировку гипотезы. | Работа с карточкой №4. Решить задачи в группе. |
| Афиширование Результаты работы групп предлагаются для рассмотрения всем участникам мастерской, организуется презентация работ учеников и Мастера, оглашение различных точек зрения на проблему | Оглашение результатов работы. Каждая группа представляет свое решение задач. Обсуждение затруднительных моментов. Карточка №5 – домашняя работа.
|
| Рефлексия Анализ движения собственной мысли, чувств, знания, мироощущения.
| Письменно ответить на вопросы: На уроке я делал… Своей работой я доволен/не доволен потому что… Этот урок показался мне… За урок я бы поставил себе, потому что… Материал урока я освоил… Мое настроение после занятия… |
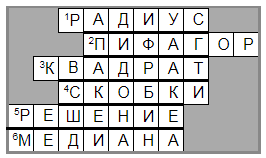
Карточка №1 «Кроссворд»
Какое слово получилось в выделенных клеточках? (Ответ: Дидона)

Карточка №2 «Задача Дидоны»
Человеку часто приходиться решать задачи, в которых нужно с помощью наименьших затрат, сил, средств, материалов получить наилучший результат. Как из круглого бревна выпилить прямоугольную балку с наименьшим количеством отходов? В каком месте следует построить мост через речку, чтобы дорога, проходящая через него и соединяющая два города, была кратчайшей?
А самая простая и самая древняя задача была такой: «Какой из всех прямоугольников заданного периметра имеет наибольшую площадь?» Решена она была древнегреческим математиком Евклидом. Все задачи такого содержания в древней Греции были объединены одним названием – «задачи Дидоны». Они названы по имени легендарной основательницы одного из старейших городов Греции и его первой царицы Дидоны.
Согласно легенде, вынужденная бежать из своего родного города, Дидона вместе со своими спутниками прибыла на северный берег Африки и хотела приобрести у местных жителей землю для нового поселения. Ей согласились уступить участок земли, однако не больше, чем объемлет воловья шкура. Хитроумная Дидона разрезала воловью шкуру на узкие ремешки, и, разложив их, сумела ограничить гораздо большую площадь, по сравнению с той, которую можно было покрыть одной шкурой. Если учесть, что царица выбирала участок, примыкающий к берегу моря, то математическую задачу, с которой она столкнулась, можно сформулировать так: какой формы должна быть кривая L, чтобы площадь фигуры, ограниченной этой кривой и заданной линией G, была наибольшей?
Ответьте на вопросы:
Кем была Дидона? С какой задачей она столкнулась?
К какому классу задач относится задача Дидоны?
Какие способы нахождения наибольшего и наименьшего значения вы знаете?
Какой из перечисленных способ более удобен для работы со сложными математическими объектами (функциями)?
Карточка №3 «Много ли земли надо?»
(По произведению Л.Н. Толстого)
Пахом давно мечтал я о земле. Работал много, поднакопил деньжат и пошел к барыне.
Барыня: Ну, что пришел?
Пахом: Землицы бы мне.
Барыня: А деньги то есть?
Пахом: Целая тысяча!
Барыня: Ну что же, сколько за день земли обойдешь, вся твоя будет за тысячу рублей. Но если к заходу солнца не вернешься на место, с которого вышел, пропали твои деньги. Согласен?
П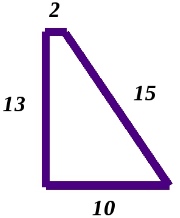 ахом: А куда же мне деваться.
ахом: А куда же мне деваться.
Барыня: Тогда пойдем.
Выбежал утром Пахом, а к вечеру прибежал на место и упал замертво без чувств, обежав четырехугольник, периметром 40 км.
Ответьте на вопросы:
Какую площадь обошел Пахом?
Мог ли Пахом обойти четырёхугольник, периметр которого был бы равен 40, но площадь была бы больше?
Составить математическую модель задачи для нахождения наибольшей площади четырёхугольника, периметр которого равен 40.
Какие методы можно использовать для нахождения максимального (минимального) значения функции?
Какой из методов наиболее универсальный? Объясните свою точку зрения. Решить задачу Пахома данным методом.
Составьте алгоритм решения задачи.
Карточка №4
Решить задачи
№ 1
На странице книги печатный текст должен занимать (вместе с промежутками между строк) 192 см2. Верхнее и нижнее поля занимают по 4 см, левое и правое – по 3 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?
Р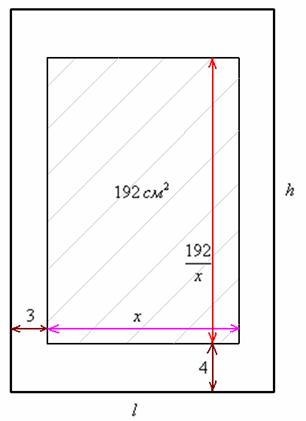 ешение
ешение
Пусть х - ширина области печати (малиновый отрезок) (можно обозначить высоту – получится равноценное решение). Тогда высота области печати:
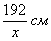 (красный отрезок).
(красный отрезок).
Ширина всего листа:
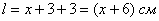
Высота: 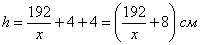
Площадь листа:
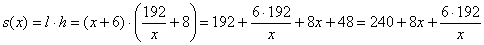
Критические точки:
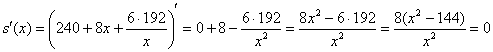
Точка 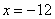 не удовлетворяет геометрическому смыслу задачи.
не удовлетворяет геометрическому смыслу задачи.
Проверим выполнение достаточного условия экстремума:
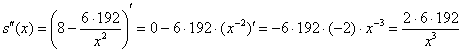
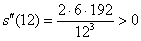 , значит, функция
, значит, функция 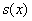 достигает минимума в точке
достигает минимума в точке 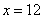 .
.
Размеры оптимального листа:
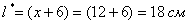 ;
;
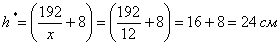
Минимальная площадь:
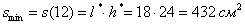
Ответ: ширина: 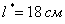 , высота:
, высота: 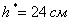 ; при этом минимальная площадь:
; при этом минимальная площадь: 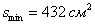
№2
На графике функции y=x2 найти точку М, ближайшую к точке А(0; 1,5).
Решение
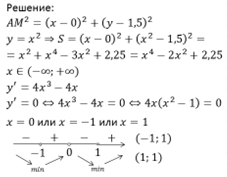
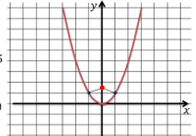
Ответ: (-1; 1), (1;1).
№3
Завод изготавливает и продает полупроводниковые приборы. Удельные расходы (в расчете на один прибор) зависят от объема производства и включают в себя постоянную часть в размере 1000 (руб/прибор) и переменную часть 2n (руб/прибор), где n − число приборов, изготовленных за месяц. Цена прибора, в свою очередь, зависит от объема производства по закону p(n)=10000−n (руб/прибор). Определить, при каком объеме производства прибыль будет максимальной?
Решение
Доход от продажи ― R(n)=np(n)=n(10000−n).
Месячные расходы при этом составляют C(n)=n(1000+2n).
Прибыль определяется формулой
P(n)=R(n)−C(n)=n(10000−n)−n(1000+2n)=9000n−3n2.
Исследуем функцию прибыли на экстремум.
P′(n)=(9000n−3n2)′=9000−6n=0,⇒n=90006=1500.
P′′(n)=(9000−6n)′=−6
Поскольку вторая производная всюду отрицательна, то решение n=1500 ― точка максимума, то есть при производстве 1500 приборов в месяц прибыль предприятия будет максимальной.
Карточка №4. Домашняя работа
№1
Таня очень любит возиться с цветами. Поэтому родители на даче выделили место под клумбу. Огородить клумбу они решили декоративным забором. Таня решила сделать клумбу прямоугольной формы. У неё есть двадцать метров забора. Давайте поможем Тане определиться со сторонами прямоугольника, чтобы площадь клумбы была наибольшей.
Решение
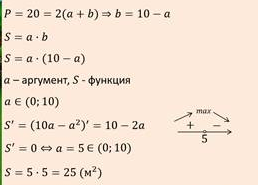
Ответ: квадрат со стороной 5.
№2
Компания изготавливает и продает 1000 изделий в месяц по цене 2000 рублей за штуку. При уменьшении цены на 50 рублей можно дополнительно продать еще 50 изделий в месяц. При какой цене фирма получит максимальный доход и каково его значение?
Решение
Пусть x ― количество вычетов по 50 рублей из базовой цены 2000 рублей.
Цена одного изделия (при продаже более 1000 изделий в месяц) ― 2000−50x.
Общее количество проданных изделий ― 1000+50x штук.
Полный доход:
R(x)=(2000−50x)(1000+50x)=2000000−50000x+100000x−2500x2=−2500x2+50000x+2000000(руб).
R′(x)=(−2500x2+50000x+2000000)′=−5000x+50000
R′(x)=0,⇒−5000x+50000=0,⇒x=500005000=10.
R′′(x)=(−5000x+50000)′=−5000.
x=10 ― точка максимума.
Доход будет наибольшим, когда число вычетов равно x=10.
Цена изделия 2000−50⋅10=1500(руб).
Объем продаж за месяц 1000+50⋅10=1500(изделий).
Максимальный доход компании составляет
Rmax=1500⋅1500=2225000(руб).








 ахом: А куда же мне деваться.
ахом: А куда же мне деваться. ешение
ешение