Уроки "Знакомство с комбинаторикой"

«Ведение в комбинаторику. Правила суммы и произведения»

Технологическая карта урока с использованием ЭОР

Герасимова Ирина Георгиевна

Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа № 38 имени Героя РФ Константинова Л. С.» города Чебоксары Чувашской Республики.

Предмет: математика

Пояснительная записка.

Тема: "Введение в комбинаторику. Правила суммы и произведения"

Место урока: начальный (1 урок в теме "Комбинаторика. Теория вероятностей")

Тип урока: урок «открытия новых знаний».

Целевая аудитория: 5-9 классы

Продолжительность: 40 минут.

Цель урока: ввести понятие науки "комбинаторика", комбинаторной задачи; познакомить с историей возникновения; показать учащимся на примерах практическое применение комбинаторики в повседневной жизни.

Задачи:

Образовательная: познакомить учащихся с правилами суммы и произведения, методом перебора для решения комбинаторных задач, формировать навыки их применения при решении простейших задач;

Развивающая: развивать математическое мышление и логическую речь учащихся; мотивацию к познанию социокультурной среды;

Воспитательная: формировать навыки самоконтроля, воспитывать чувство ответственности за качество и результата выполняемой работы, вырабатывать партнерские отношения.

Методы обучения: проблемный, частично – поисковый, объяснительно – иллюстративный, исследовательский.

Планируемые результаты:

Используемые формы организации познавательной деятельности учащихся: коллективная форма работы, групповая, индивидуальная работа.

Оборудование и основные источники информации: компьютер, проектор, экран, авторская презентация к уроку, рабочая тетрадь, раздаточный материал (листы с заданием, карточки с задачами, шаблон буклета).

Ход урока

I. Организационный момент. Мотивация. Игра с рукопожатиями и подсчетом полученных комбинаций.

II. Активизация познавательной деятельности

Постановка проблемы урока:

Сценка.

- Холмс, это кажется, по вашей части

- Дорогой Ватсон, у Вас на подносе коробки с соком? Но, Вы же знаете, я не пью сок!

- Холмс мне просто нужен Ваш совет. Понимаете, я вчера, налив в равных количествах в стакан соки из двух коробок получил прекрасный коктейль. Теперь чтобы снова найти нужное сочетание, мне, очевидно, придется попробовать кучу вариантов. Но очень боюсь, что заболит живот.

- Не волнуйтесь, Ватсон, Вам в худшем случае придется попробовать шесть вариантов коктейлей. Хотя, может быть, вам повезет и нужный коктейль появится раньше последней из возможных комбинаций. В противном случае, если после проведения всех опытов у вас разболелся живот, то вам останется утешиться мыслью, что пострадали за науку.

- Вы смеетесь, Холмс? О какой науке может идти речь в подобной ситуации?

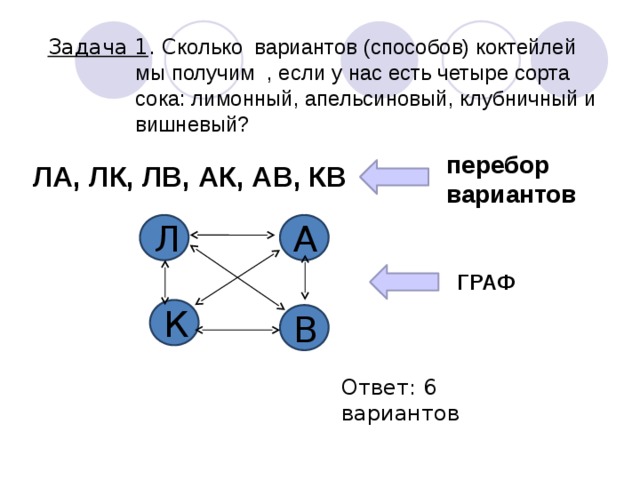
- Речь идет о комбинаторике – разделе науки, в котором рассматриваются задачи – подсчете числа комбинаций, составленных из некоторых элементов по определенным правилам. Вот Вы сейчас, Ватсон, столкнулись с элементарной комбинаторной задачей: «Сколько существует способов составить коктейль из двух напитков, взятых в равных количествах, если у вас имеется четыре сорта сока?»

- И как Вы так быстро решили задачу?

- Эта задача решается элементарно Ватсон!

Ну что, ребята, поможем Ватсону решить эту задачу? Итак, сколько же вариантов (способов) мы получим с вами, если у нас есть четыре сорта сока: лимонный, апельсиновый, клубничный и вишневый?

Ученики решают задачу и один около доски.

Л, А, К, В. Варианты: ЛА, ЛК, ЛВ,

АК, АВ, КВ.

Учитель:

Шерлок Холмс и доктор Ватсон столкнулись с так называемыми комбинаторными задачами. Сегодня на уроке мы познакомимся с разделом математики, который позволяет ответить на вопросы "Сколькими способами... " или "Сколько вариантов..." Так что же изучает комбинаторика? Давайте запишем определение этой науки в наши буклеты, которые мы будем заполнять в течение нашего занятия.

Итак, кто запомнил, что такое комбинаторика? Выслушав ответы, записываем: Комбинаторика – раздел математики, в котором рассматриваются задачи о подсчете числа комбинаций, составленных из некоторых элементов по определенным правилам. Задача комбинаторики – это задача размещения объектов по специальным правилам и нахождение числа способов таких размещений. Особая примета комбинаторных задач – вопрос, который можно сформулировать так, чтобы он начинался словами «Сколькими способами…»

"Учимся не для школы, а для жизни" (Сенека Люций Анней - римский философ и поэт). Эти слова, я хочу взять эпиграфом к нашему уроку. Так как при изучении нового материала ребята часто задают вопросы: "А зачем она нужна?", "Может ли она чем-то помочь в реальной жизни?"

Поэтому для начала предлагаю поиграть в игру.

Игра "Верите ли вы, что..."

Я выслушала ваше мнение и в конце урока мы вернемся к этим вопросам.

III. Подготовка к основному этапу изучения нового материала.

Учитель: В старинных русских сказаниях повествуется, как богатырь, доехав до распутья, читает на камне: "Вперёд поедешь – голову сложишь, направо поедешь – меча лишишься”. А дальше уже говорится, как он выходит из этого положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации. И целый раздел математики, именуемый комбинаторикой, занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из этих комбинаций выбрать наилучшую.

Из истории.

С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов – во время битвы, инструментов – во время работы. Первые упоминания о вопросах близких к комбинаторным, встречаются в китайских рукописях 12-13 вв до н.э. В древней Греции изучали фигуры, которые можно было составить из частей квадрата, разрезанного особым образом. Позже появились такие игры как нарды, карты, шашки, шахматы и т.д. В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных. Не только игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв с использованием ключевых слов и т. д. Многие ученые проводили исследования по комбинаторике. И только в 1666 г. была опубликована работа Готфрида Вильгельма Лейбница «Об искусстве комбинаторики». С этого момента комбинаторику рассматривают как самостоятельный раздел математики.

Задача, в которых идет речь о тех или иных комбинациях объектов, называются комбинаторными. Область математики, в которой изучаются комбинаторные задачи, называются комбинаторикой.

И сегодня мы научимся находить возможные комбинации для решения элементарных комбинаторных задач и рассмотрим сферы их применения. Продуктом нашей совместной деятельности станет выпуск буклета "Комбинаторика в нашей жизни".

IV. Открытие нового знания.

Учитель: Скажите, а вам приходиться делать выбор, подсчитывать способы? В каких ситуациях?

Представим ситуацию: мама отправляет вас в магазин купить что-нибудь к чаю. В магазине 8 сортов печенья, 10 сортов конфет, 17 сортов конфет и 3 вида тортов. сколько вариантов выбора покупки вы имеете?

Данная задача является элементарной комбинаторной задачей. Какие действия необходимо по вашему выполнить для ее решения? (правило сложения).

Учитель: А теперь рассмотрим другие виды задач. У каждой из вас пары есть задача и все необходимые инструменты для практического ее решения. Приступайте. Примеры задач:

Уважаемая миссис Хадсон к нам придут гости. В качестве вторых блюд приготовьте мясо, котлеты и рыбу. На сладкое – мороженое, фрукты и пирог. Гость выбирает одно второе блюдо и одно блюдо на десерт. Подсчитайте, сколько будет гостей, и поставьте необходимое количество стульев. Очень вас прошу, чтобы количество стульев соответствовало количеству приглашенных.

Давайте поможем миссис Хадсон.

Мясо - фрукты мясо - мороженое мясо - пирог.

Котлеты-фрукты котлеты - мороженое котлеты - пирог.

Рыба – фрукты рыба - мороженое рыба – пирог.

Следовательно, необходимо поставить 9 стульев.

1. Государственные флаги некоторых стран состоят из трёх горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику, при условии, что у каждой страны свой отличный от другой, выбор полос.

2.Изменяя порядок слов: мою, руки, я, составьте всевозможные предложения.

3.Предположим, что имеется белый хлеб, черный хлеб, сливочное масло, сыр, колбаса и шпроты. Сколько бутербродов можно приготовить? (Без повторения продуктов)

Эти задачи мы решили методом перебора возможных вариантов. Этот способ прост для небольшого количества элементов. А что делать в остальных случаях? Давайте размышлять. Что общего есть при решении данных задач? Сформулируйте правило для решения данных задач.

(Решение задач оформляется в рабочей тетради)

V. Первичное осмысление и применение нового знания.

Холмс мягко улыбнулся: « Послушайте Ватсон, мне вчера подарили книгу баснописца Крылова, и я смог познакомиться с любопытной басней « Квартет».

Проказница Мартышка,

Осел, козел,

Да косолапый Мишка,

Затеяли играть квартет.

Ударили в смычки, дерут, а толку нет.

«Стой, братцы, стой!- кричит Мартышка-

Погодите!

Как в музыке идти? Ведь вы не там сидите».

И замечательная мораль у этой басни. В содержание этой басни прячется симпатичная задача, и связана она с комбинаторикой.

Послушайте и решите эту задачу: « Сколькими способами могут сесть крыловские музыканты? Подсчитайте число возможных вариантов посадки артистов в квартете». Применяя правило произведения, ребята объясняют и считают число возможных вариантов.

Ну что молодцы ребята справились с задачей.

VI. Закрепление знаний и способов действий.

Просмотр слайдов "Применение комбинаторики ".

Учитель: Каждый из нас хочет быть востребован в жизни. Представите, что вы решили заняться бизнесом (частный ресторан, туристическое агентство, спортивный клуб). Для того, чтобы ваше заведение было конкурентоспособным необходимо знать, что ваших клиентов интересует больше всего. Учитель: навыки решения комбинаторных задач в дальнейшем помогут вам творить, думать необычно, оригинально, смело, видеть то, мимо чего вы часто проходили не замечая, любить неизвестное, новое; преодолевать трудности и идти через невозможное вперед.

Математика повсюду –

Глазом только поведешь

И примеров сразу уйму

Ты вокруг себя найдешь…

Я предлагаю вернуться к нашей игре "Верите ли вы, что..." и переосмыслить свои ответы.

VII. Рефлексия.

Учитель: Так может ли комбинаторика помочь в реальной жизни? В чем?

Я рада слышать ваши ответы. Я сегодня увидела в вас энергичных, предприимчивых, ярких личностей. Я уверена, что каждый из вас найдет достойное место в жизни.

VIII. Домашнее задание. Придумайте несколько комбинаторных задач.

ЗНАКОМСТВО С КОМБИНАТОРИКОЙ

"Учимся не для школы, а для жизни"

(Сенека Люций Анней - римский философ и поэт)

Тема урока: Знакомство с комбинаторикой.

Эпиграф урока:

«Учимся не для школы, учимся для жизни»

Сенека Люций Анней - римский философ и поэт

Комбинаторика – раздел математики , в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Задача комбинаторики – это задача размещения объектов по специальным правилам и нахождение числа способов таких размещений.

Особая примета комбинаторных задач – вопрос, который можно сформулировать так, чтобы он начинался словами «Сколькими способами…»

Прямо поедешь – голову сложишь,

направо поедешь – коня потеряешь,

налево поедешь – меча лишишься

Выбирали наилучшее расположение

• охотников во время охоты;
• воинов во время битвы;
• инструментов во время работы;
• украшений на одежде;
• узоров на керамике;
• перья в оперении стрелы …

Магические и латинские квадраты .

Позже появились шашки, шахматы, нарды, японские шашки Го и др. игры.

В каждой из этих игр рассматривали различные сочетания передвигаемых фигур.

Выигрывал тот, кто их лучше изучил, знал выигрывающие комбинации и умело избегал проигрывающих.

Комбинаторные навыки были полезны в играх, требовавших умения рассчитывать, составлять планы и опровергать планы противника

Не нужно нам владеть клинком,

Не ищем славы громкой .

Тот побеждает, кто знаком

С искусством мыслить тонким.

Вильям Уордсворт

Иероглифы и клинопись

Комбинаторные навыки

в разгадывании сложных шифров помогли французскому филологу

Жану Франсуа Шампольону прочитать иероглифы, которыми писали египтяне еще до того, как возникла наука у древних греков;

Химический пасьянс

17февраля 1869 г. был открыт периодический закон элементов .

«Искать же чего-нибудь, хотя бы грибов, или какую-нибудь зависимость, нельзя иначе, как смотря и пробуя»

Д.И.Менделеев

Исследования по комбинаторике проводили:

Никколо Тарталья

Джероламо Кардано

(1499 – 1557)

Галилео Галилей

( 1564 – 1642)

Блез Паскаль

(1623 – 1662)

Пьер Ферма

(1601 – 1665)

1666 г. – опубликована работа Готфрида Вильгельма Лейбница «Об искусстве комбинаторики».

С этого момента комбинаторику рассматривают как самостоятельный раздел математики

Задача 1 . С колько вариантов (способов) коктейлей мы получим , если у нас есть четыре сорта сока: лимонный, апельсиновый, клубничный и вишневый?

перебор вариантов

ЛА, ЛК, ЛВ, АК, АВ, КВ

Л

А

ГРАФ

К

В

Ответ: 6 вариантов

Граф-дерево

меню

мясо

МФ, ММ, МП, РФ, РМ, РП, ОФ, ОМ, ОП

меню

мясо

Задача 3. Мама отправляет вас в магазин купить что-нибудь к чаю. В магазине 8 сортов печенья, 10 сортов карамели, 17 сортов шоколадных конфет и 3 вида тортов. Сколько вариантов выбора покупки вы имеете?

Решение:

8+10+17+3=38 возможных вариантов покупки

Правило суммы

• Если элемент А может быть выбран m способами, а элемент В – n способами, причем выборы А и В являются взаимно исключающими, то выбор «либо А, либо В» может быть осуществлен m+n способами.
• Задача 2. На одной полке книжного шкафа стоит 30 различных книг, а на другой – 40 различных книг (не такие как на первой). Сколькими способами можно выбрать одну книгу?
• Решение: 30 + 40 = 70 (способами).

Задача 4 . Государственные флаги некоторых стран состоят из трёх горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику, при условии, что у каждой страны свой отличный от другой, выбор полос.

Задача 5 . Предположим, что имеется белый хлеб, черный хлеб, сливочное масло, сыр, колбаса и шпроты. Сколько бутербродов можно приготовить? (Без повторения продуктов)

Правило произведения

Если элемент А может быть выбран m способами, а элемент В – n способами, то выбор А и В может быть осуществлен m*n способами

14

Методы решения комбинаторных задач

• 1. Перебор возможных вариантов.
• 2. Графы.
• 3. Граф - дерево.
• 4. Правило суммы.
• 5. Правило произведения

Завучу, составляющему расписание уроков

учителю , распределяющему различные виды работ между группами учащихся,

конструктору, разрабатывающему новую модель механизма,

ученому-агроному,

планирующему распределение сельскохозяйственных культур на нескольких полях

химику, изучающему строение органических молекул, имеющих данный атомный состав.

• Комбинаторика изучает:

• деятельность комбинатов бытового обслуживания,
• способы пошива комбинезонов,

• способы решения задач на различные комбинации объектов.

2. Комбинаторные задачи встречаются в профессиональной деятельности:

• парикмахера-визажиста,
• диспетчера автовокзала,
• завуча школы,
• экономиста,
• повара (добавьте свой пример)

3. Изменяя порядок слов: Россию, люблю, я , составьте всевозможные предложения.

ТЕСТ:

Люди, которые умело владеют техникой решения комбинаторных задач, а, следовательно, обладают хорошей логикой, умением рассуждать, перебирать различные варианты решений, очень часто находят выходы, казалось бы, из самых трудных безвыходных ситуаций.

Пример - сказочный герой Барон Мюнхгаузен, который находил выход из любой сложной и трудной ситуации.

Но и в жизни эти умения очень часто помогают человеку