Задания с производной при подготовке к ЕГЭ Задания В8 и В14

Задания с производной при подготовке к ЕГЭ

Задания В8 и В14

Типы заданий

• Геометрический смысл производной

• Касательная в точке
• Касательная в точке

• Механический смысл производной
• Промежутки возрастания-убывания
• Локальные экстремумы
• Наибольшие/наименьшие значения на отрезке

Геометрический смысл производной (теория)

• Следующие величины равны

• Значение производной f’(x 0 ) в точке x 0 Тангенс угла наклона касательной к графику функции y= f (x 0 ) в точке x 0 Угловой коэффициент касательной к графику функции y= f (x 0 ) в точке x 0
• Значение производной f’(x 0 ) в точке x 0
• Тангенс угла наклона касательной к графику функции y= f (x 0 ) в точке x 0
• Угловой коэффициент касательной к графику функции y= f (x 0 ) в точке x 0

1. Вычислить производную

2. Вычислить производную

3. Вычислите величину √3 f’ (3)

4 . Точка касания

• На рисунке изображен график производной функции y= f (x) . Прямая y= 2 x+1 является касательной к графику этой функции. Найдите ординату точки касания.

5. Точка касания

• На рисунке изображен график производной функции y= f (x) . Прямая y= 3 x -4 является касательной к графику этой функции. Найдите ординату точки касания.

Задачи 6-8

• Касательная к графику функции y= 3 – 2 x – x 2 параллельна прямой y= 4x . Найдите абсциссу точки касания .

• Касательная к графику функции y= 3 – 2 x – x 2 проходит через точки А(1, 1) и В(-1, 5) . Найдите абсциссу точки касания
• Найдите положительное значение параметра b , при котором прямая y= -3 является касательной к графику функции y= 2 x 2 + bx – 1 .

Задачи 9 - 12

• Прямая y= x+ 2 является касательной к графику функции y= а x 2 – х + 6 . Найдите а .
• Прямая y= 2 x является касательной к графику функции y= - x 2 +7х + с . Найдите с .
• Прямая y= kx + b является касательной к графику функции y= - x 2 +4х - 1 в точке А(1,2) . Найдите b .

• Касательная к графику функции y= x ( x-2) проходит через точки А(1, -2) и В(-3, 6) . Найдите ординату точки касания

Механический смысл производной

• Если s(t) – функция, задающая закон движения материальной точки (пройденный путь в зависимости от времени), то v(t)=s’(t) – мгновенная скорость точки

Движение материальной точки

• Материальная точка движется прямолинейно по закону s(t)=1/3 t 3 + ½ t 2 – 9t +1 , где s – расстояние от точки отсчета в метрах, а t – время в секундах с начала движения. Через сколько секунд после начала движения скорость точки будет равна 3 м/с?
• Материальная точка движется прямолинейно по закону s(t)=6 + 2t – 0,25t 2 , где s – расстояние от точки отсчета в метрах, а t – время в секундах с начала движения. Через сколько секунд после начала движения точк а остановится?
• Материальная точка движется прямолинейно по закону s(t)= 4 + 2t – t 2 , где s – расстояние от точки отсчета в метрах, а t – время в секундах с начала движения. Какова была начальная скорость точки (в м/с)?

Промежутки возрастания-убывания

• Определение возрастающей (убывающей) функции на промежутке
• Функция является возрастающей на промежутке ↔ когда ее производная положительна в любой точке промежутка
• Функция является убывающей на промежутке ↔ когда ее производная отрицательна в любой точке промежутка

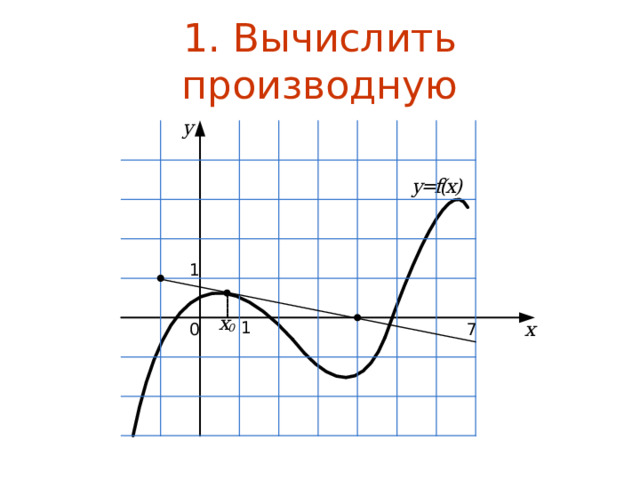
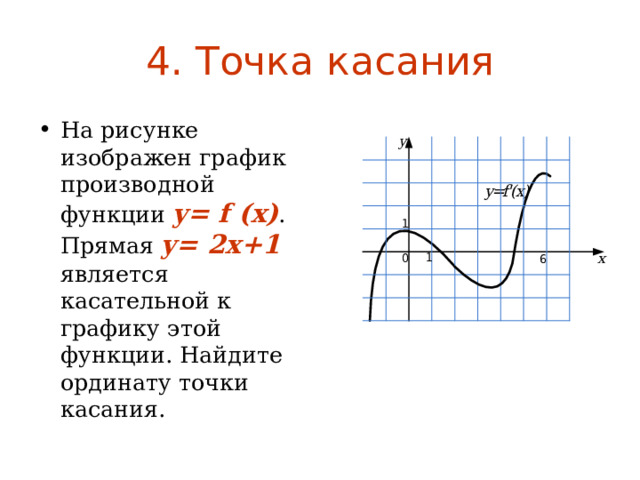
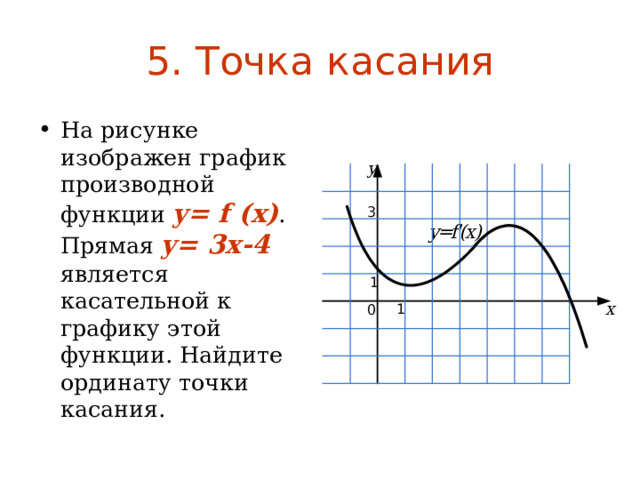
Возрастание/убывание

• На рисунке изображен график функции y = f ( x ) . Определите количество целых точек на интервале [-1; 9], в которых производная функции отри­цательна.

Возрастание/убывание

• На рисунке изображен график функции y = f ( x ) . Определите количес­тво целых точек на интервале [ 0 ; 9], в которых касательная к графику функции параллельна прямой y = 4 .

Возрастание/убывание

• На рисунке изображен график функции y = f ( x ). Определите , в какой точк е промежутка [ 5 ; 9] функция принимает наибольшее значение?

Возрастание/убывание

• На рисунке изображен график производной функции y = f ( x ) . Найдите промежутки возрастания данной функции, принадлежащие отрезку [-1,5; 12,5] . (В ответе укажите общее число целых точек на этих промежут­ках).

Возрастание/убывание

• На рисунке изображен график производной функции y = f ( x ) . Найдите сумму целочисленных абсцисс точек, лежащих на отрезке [0; 12] , в которых данная функция убывает.

Возрастание/убывание

• Найдите количество промежутков убывания функции y = f ( x ) , если ее производная имеет вид f’ ( x ) = (x 2 – 1)(x 2 – 9)(x – 4) 2

Локальные экстремумы

• Определение максимума (минимума) функции
• Точка х 0 является точкой максимума функции y = f ( x ) , если f ’ ( x 0 ) =0 и при переходе через эту точку производная меняет знак с плюса на минус.
• Точка х 0 является точкой минимума функции y = f ( x ) , если f ’ ( x 0 ) =0 и при переходе через эту точку производная меняет знак с минуса на плюс.

Локальный экстремум

• На рисунке изображен график производной функции y = f ( x ) . Найдите целое положительное число n такое, что максимум функции f ( x ) лежит на отрезке [n,n+1] .

Локальный экстремум

• На рисунке изображен график производной функции y = f ( x ) . В точке максимума к графику функции проведена касательная, пересекающая ось у в точке с ординатой -1 . Найдите сумму абсциссы и ординаты точки касания.

Локальный экстремум

• На рисунке изображен график производной функции y = f ( x ) . В точке максимума к графику функции f ( x ) проведена касательная, пересекающая ось у в точке с ординатой 2,5 . Найдите сумму абсциссы и ординаты точки касания.

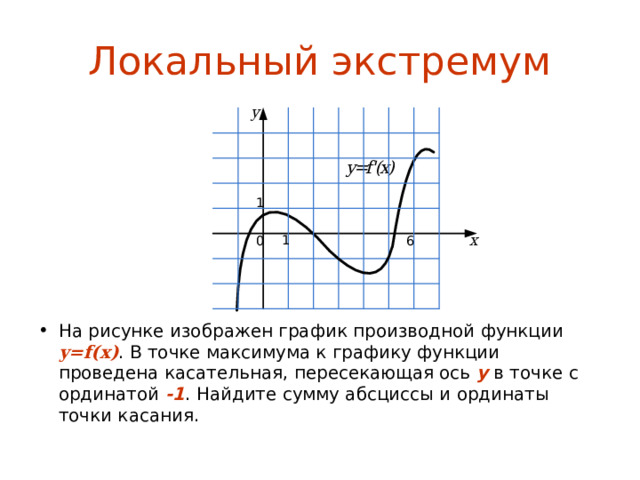
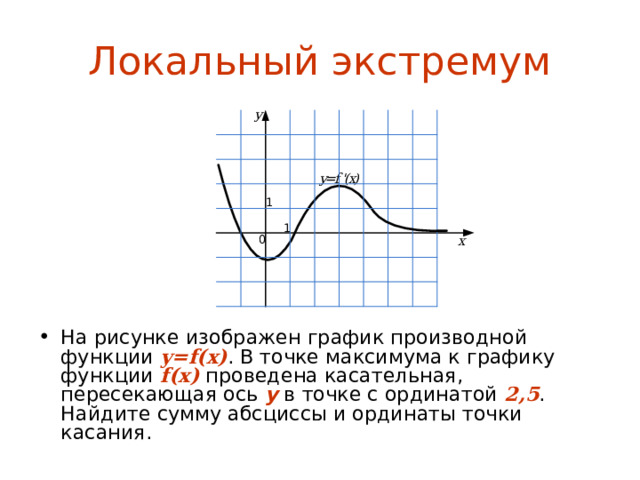
Локальный экстремум

• На рисунке изображен график производной функции y = f ( x ) . Сколько минимумов имеет данная функция на отрезке [-1; 6] ?

Локальный экстремум

• Найдите количество точек максимума функции y = f ( x ) , если f’ ( x ) = (x 2 + 3x – 4)(x 2 – 16)(x 2 – 1)

Экстремумы на отрезке

• Наибольшее значение функции на отрезке находится как наибольшее из локальных максимумов и значений на границах
• Наименьшее значение функции на отрезке находится как наименьшее из локальных минимумов и значений на границах

Экстремумы на отрезке

• Найдите точку, в которой функция y = 2x 3 + 9x 2 – 60x +1 принимает наибольшее значение на промежутке [-6; 6] .
• Найдите значение функции y = 1/4x 4 - 2x 2 +5 в точке максимума
• Найдите наименьшее значение функции y= π /√3 - √3 x – 2 cosx + 11 на отрезке [0; π /2 ]

Экстремумы на отрезке

• Найдите количество целых значений а, при которых функция y = -x 3 /3 + (a+2)x 2 – 4x +10 не имеет точек экстремума.
• Найдите количество целых значений функции y = х + 1 6 / (х-1) на отрезке [-4; 0]
• Найдите наименьшее значение функции y=2 2x + 2 x+1 – xln16 + 3 на отрезке [-1;2]
• Найдите наименьшее значение функции y=x|x 2 + 2x – 3| + (x-1) 2 на отрезке [-2; 0]