Действия над комплексными числами в тригонометрической форме (для ДО)

Тема: « Действия над комплексными числами в тригонометрической форме»

1. Актуализация ранее полученных знаний и умений.

Сначала повторим то, что уже было изучено ранее, вспомним ещё раз как геометрически изображаются комплексные числа (далее буду писать к.ч.), как выполняются операции над к.ч. в алгебраической форме (см. предыдущий конспект к уроку). Все задания записывайте в рабочую тетрадь!

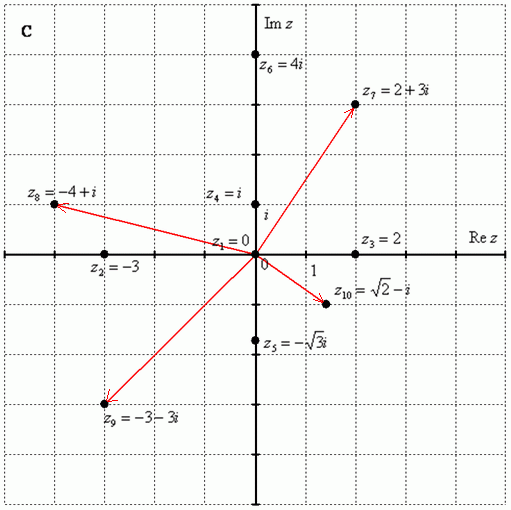
Задание №1. Изобразим следующие комплексные числа: (значит координата х=0, координата у=0), (отметим точку с координатами х=-3, у=0), ( х=2, у=0), (х=0, у=1), (х=0, у=- корень из 3), ( х=0, у=4), ( точка с координатами(-4;1) ), ( точка с координатами (-4;1) ), ( точка с координатами (-3;-3) ), ( точка с координатами (корень из 2; -1) )

Задание№2. Выполнить сложение к.ч. ,

Решение: Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Задание №3.Найти разности к.ч. и , если ,

Решение: Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

, т.е. можно записать в виде .

Рассчитаем вторую разность: .

Задание №4. Найти произведение комплексных чисел ,

Решение: Очевидно, что произведение следует записать так: , главное, помнить, что и быть внимательным.

Это и есть ответ.

!Надеюсь, всем было понятно, что

! В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

2. Далее, перейдем к рассмотрению новой темы. На прошлом уроке, мы уже записали тригонометрическую форму к.ч. Рекомендую посмотреть видео-урок (5мин) «Тригонометрическая запись комплексного числа», перейдя по ссылке https://www.youtube.com/watch?v=ORr7P-sNJqc (в тетрадь можно не записывать видео-урок).

3. Сформулируем основные формулы для выполнения действий над к.ч. в тригонометрической форме. Весь ниже изложенный материал запишите в рабочую тетрадь. (это можно сделать в виде памятки)

Памятка№1

Рассмотрим примеры перехода к.ч. изалгебраической в тригонометрическую форму (записать в рабочую тетрадь)

3.1.Представить в тригонометрической форме комплексные числа: , , , .

Решение:

1. Представим в тригонометрической форме число .

Найдем его модуль и аргумент. . Поскольку (случай 1 (см. видео-урок)), то . Таким образом: – число в тригонометрической форме.

2. Представим в тригонометрической форме число .

Найдем его модуль и аргумент Поскольку (случай 2), то – вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение , поэтому в подобных случаях аргумент приходится оставлять в громоздком виде: – число в тригонометрической форме.

3. Представим в тригонометрической форме число .

Найдем его модуль и аргумент. . Поскольку (случай 3), то .

Таким образом: – число в тригонометрической форме.

4. Представим в тригонометрической форме число .

Найдем его модуль и аргумент.

Поскольку (случай 1), то (минус 60 градусов).

Таким образом: – число в тригонометрической форме.

!А вот здесь, минусы не трогаем.

Любое комплексное число (кроме нуля) можно записать в показательной форме: , где – это модуль комплексного числа, а – аргумент комплексного числа.

Что нужно сделать, чтобы представить комплексное число в показательной форме? Почти то же самое: найти модуль и аргумент. И записать число в виде .

Памятка№2 (как представить к.ч. в показательной форме)

Рассмотрим пример записи к.ч. в показательной форме.

Например, для числа предыдущего примера у нас найден модуль и аргумент: , . Тогда данное число в показательной форме запишется следующим образом: z_{2 =}2√5×e^i(П-arctg2).

Например, число в показательной форме будет выглядеть так: z₄=2×e^i(-П/3)

Например, число в показательной форме будет записываться так: z₁=2√3×e^iП/6

Сделаем вывод, что комплексное число в показательной форме записывается строго по форме .

Памятка№3 (как возвести к.ч. в степень)

Рассмотри примеры возведения комплексных чисел в степень

а) возвести в степень комплексные числа , ,

Решение: Здесь тоже всё просто, главное, помнить знаменитое равенство:

Если мнимая единица возводится в четную степень, то техника решения такова: i¹⁰= (i²)⁵ = (-1)⁵ = -1

Если же, мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень: i³³= i×i³² = i×(i²)¹⁶ = i×(-1)¹⁶ = i×1 = i

Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить: (-i)²¹= (-1)²¹×i²¹ = -1×i ×i²⁰ = -i×(i²)¹⁰ = -i×(-1)¹⁰ = -i×1 = - i

4. Если остались вопросы по изучению темы, можно более подробно еще раз рассмотреть теоретический и практический материал используя ссылку http://ru.solverbook.com/question/dejstviya-nad-kompleksnymi-chislami-v-trigonometricheskoj-forme/

5. Домашнее задание: пройти тест, https://multiurok.ru/tests/kompleksnye-chisla-deistviia-nad-kompleksnymi-chislami.html