Вычисление интегралов. Непосредственное интегрирование. ( для ДО )

1. Основные понятия. (Актуализация)

Прежде чем рассмотреть примеры вычислений определённых интегралов, вспомним с прошлого урока, что интегралы бывают неопределённые и определённые.

Нахождение простейшего интеграла сводится к нахождению общего вида первообразной. Результатом неопределённого интеграла является функция.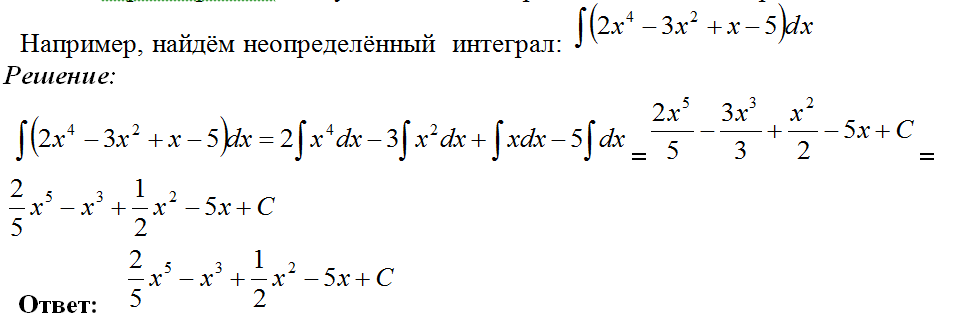

Вычисление простейшего определённого интеграла сводится к применению формулы Ньютона-Лейбница. Существует несколько методов нахождения интегралов:

• Непосредственное интегрирование
• Метод замены переменной
• Интегрирование почастям.

В общем виде определенный интеграл записывается так: ,где нижний предел интегрирования стандартно обозначается буквой , верхний предел интегрирования стандартно обозначается буквой . Отрезок называется отрезком интегрирования.

Ответим на следующие вопросы:

Что такое определенный интеграл?

Определенный интеграл – это число.

Есть ли у определенного интеграла геометрический смысл?

Есть. Самая популярная задача – вычисление площади с помощью определенного интеграла.

Что значит решить определенный интеграл?

Решить определенный интеграл – это значит, найти число.

Как решить определенный интеграл?

С помощью знакомой уже формулы Ньютона-Лейбница:

Этапы решения определенного интеграла следующие:

• Сначала находим первообразную функцию (неопределенный интеграл). Обратите внимание, что константа в определенном интеграле не добавляется. Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ? Подготовка для применения формулы Ньютона-Лейбница.

• Подставляем значение верхнего предела в первообразную функцию: .

• Подставляем значение нижнего предела в первообразную функцию: .
• Рассчитываем (без ошибок!) разность , то есть, находим число.

Всегда ли существует определенный интеграл?

Нет, не всегда.

Рассмотрим пример вычисления интеграла , его не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными).

Может ли определенный интеграл быть равен отрицательному числу?

Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл.

Рассмотрим основные свойства определённого интеграла

Теорема 1.

Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.

Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница:

Теорема 2. Постоянный множитель можно выносить за знак определённого интеграла, т.е.

Теорема 3. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.

Теорема 4. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если

то

Теорема 5. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.

2. Рассмотрим примеры вычисления интегралов.

Пример 1. Вычислить определённый интеграл

Решение: Сначала найдём неопределённый интеграл, т.е. представим подынтегральную функцию в виде степени (заменив корень), получим х^1/3, а затем найдем первообразную этой функции:

Применяя формулу Ньютона-Лейбница к первообразной получим

Ответ: 12.

Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл.

Пример 2. Вычислить определённый интеграл

Решение: Вспомним, что е^2х - функция сложная, а значит при нахождении первообразной ( интеграла) нужно умножить на обратный коэффициент который стоит перед х, т.е. на ½. Используя формулу

получим,

Пример 3. Вычислить определенный интеграл

Решение:

Объяснение:

(1) Выносим константу за знак интеграла.

(2) Интегрируем по таблице с помощью самой популярной формулы . Появившуюся константу 1/3 целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?

(3) Используем формулу Ньютона-Лейбница . Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ 4²/₃

Ответ: 4²/₃

Пример 4. Вычислить определённый интеграл

Решение:

3. Далее рассмотрим еще примеры вычисления определённых интегралов, для этого посмотрите видео-урок https://videouroki.net/video/18-vychislenie-integralov.html. Если видео-урок будет пропущен, то будет намного сложнее выполнить домашнее задание.

Важно! Все интегралы, входящие в домашнюю работу, являютсяпростейшими интегралами.