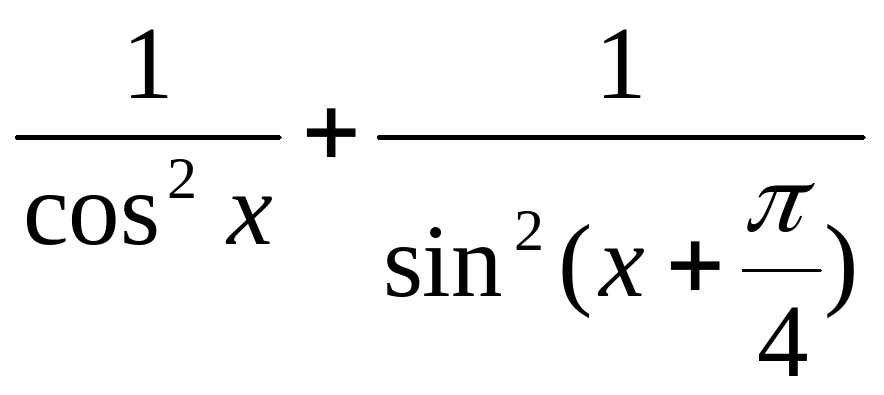Получите доступ к огромной базе учебных материалов на каждый урок с возможностью удалённого управления...

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 21.02.2025 08:48

Гоптарь Лидия Ивановна

Преподаватель высшей математики

69 лет

17 376

1 948

Подписчики

Подписки

Местоположение

Россия, воронеж

Специализация

Математика

Обо мне Блог Файлы Тесты Галерея Активность Награды

10 класс. Производная функции.

Категория: Математика

21.04.2020 14:46

" МНЕ приходится делить время между политикой и математикой.

Однако математика гораздо важнее."

А.Эйнштейн

Просмотр содержимого документа
«10 класс. Производная функции.»

КОУ ВО «ЦЛПДО»

Разработка уроков- консультаций по математике в 10 классе.

( 8 уроков).

Подготовила учитель математики Гоптарь Л. И.

Производная функции.

Обобщающие уроки – консультации в 10 классе.

Цели уроков – консультаций:

Обобщить знания учащихся по теме «Производная функции» и выяснить степень готовности учащихся.
Способствовать развитию навыков применения теоретических знаний в практической деятельности.
Способствовать воспитанию ответственности за качество и результат выполняемой работы на уроке.

Задачи :

Повторить алгоритм нахождения производной.
Используя правила нахождения производной, применить их для решения конкретных задач.
Сформировать глубину и оперативность мышления.

Планируемый результат уроков - консультаций:

Учащиеся знают правила нахождения производных и готовы к выполнению конкретных упражнений.
Учащиеся отработали навыки применения теоретических знаний расчета производной функции на учебных примерах.
Учащиеся почуствовали ответственность за качество и результат выполняемой работы

на уроках.

Тип уроков - консультаций: уроки повторения и обобщения знаний.

Ход уроков:

Организационный момент.

Постановка целей и задач уроков - консультаций.

2) Повторение теоретического материала.

Учитель:

«Вы уже накопили некоторый опыт нахождения производной.

И сегодня мы посмотрим, чему же вы научились.

Повторим теоретический материал: отвечаем на вопросы».

-а) что такое производная?

-б) какие смыслы производной существуют?

-в) что такое производная с геометрической точки зрения?

-г) какой угол образует прямая с осью абсцисс:

если k0

если k
если k=0
если прямые a || в?

д) что такое производная с механической точки зрения?

е) что значит продифференцировать?

ж) какая функция называется дифференцируемой в точке ?

з) что такое критические точки?

и) какую формулу имеет уравнение касательной?

3)Применение теоретического материала к решению задач.

4)Обязательно повторяем формулы.

«Рассмотрев теоретический материал вычисления производной, применим его при решении задач».

- Решаем следующие упражнения.

-Задания по индивидуальным карточкам.

Найдите производную функции.

y=3x	y=- +5	y=sin²x	y=cos3x
y=4x²	y=	y=cos²2x	y=cos(4x-1)
y=x^-5	y=	y=	y=ctg(x- )
y=	y=	y=4x²+	y=tg( -2x)
y=	y=4-x⁴	y=	y=
y=x²+3sinx	y=	y=cos2x
y=3x²+2x+5	y=	y=

После решения этих примеров предлагаю следующее задание для устного счета.

Учащиеся опять-таки выполняют строго индивидуальные задания по карточкам: стрелками устанавливают соответствие между левым и правым столбцами таблицы, то есть самостоятельно устанавливают соответствие…

Установите соответствие.

Функция

1. +2

2. x+cosx

3. sin²x

4. cos2x

Производная

А. 1-sinx

C. -2sin2x

D. sin2x

Далее следующие задания для устного счета.

Учащиеся выполняют их также самостоятельно.

Производная какой функции равна:

Задайте формулой функцию h,

если f(x)=3-2x, g(x)=x²,p(x)=sinx

1. 2x+4

2. 6x+1

3. 16x³-4

4. 8x-2

5. 9x²-

a) h (x)=g(f(x))

b) h (x)=g(p(x))

c) h (x)=p(f(x))

- «Провожу контроль усвоенного материала. Для этого всегда пишу образец решения, выполненный на оценку «5».

При этом, решив примеры варианта, нужно указать на листе его номер, номер примера, и, найдя в таблице классификатор правильного ответа (1-4), указать его код.

Таким образом, в итоге на листе в качестве ответов должен быть отображен номер варианта и столбец из ответов – а) 2 б) 4 и т.д.

На выполнение задание дается 5-10 минут».

В это время на интерактивной доске отображается задание программированного контроля и таблица с вариантами ответа. В данном уроке запланировано проведение трех последовательных самостоятельных работ по системе программированного контроля.

Найти производную функции. Программированный контроль.

Самостоятельная работа №1.

I вариант	II вариант
a. f(x)=sin2x-cos3x	a. f(x)=cos2x-sin3x
b. f(x)=tgx-ctg(x+ )	b. f(x)=ctg(x)+tg(x+ )
c. f(x)=sin²x	c. f(x)=cos²x

Варианты ответов

1	2	3	4
cos2x-sin3x	2sin3x-3cos3x	-2sin2x-3cos3x	2cos2x+3sin3x

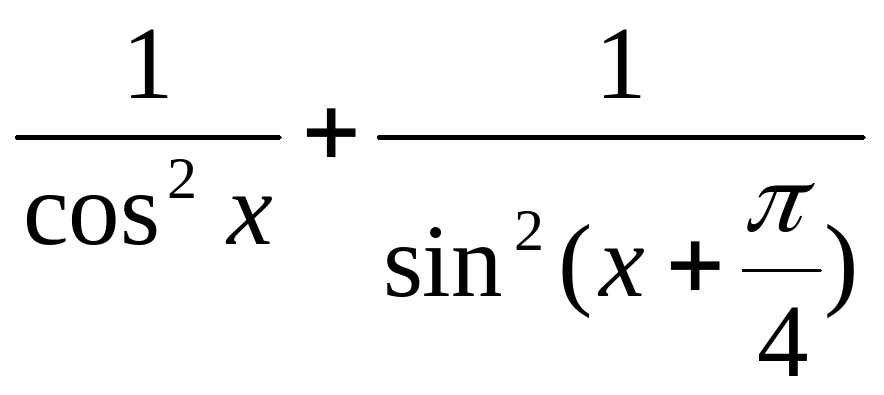
-2sinxcosx	-2sin2x	sin2x	2cosx

После выполнения учащимися каждого задания программированного контроля ученики в паре обмениваются листами. Учитель сообщает коды правильных ответов, и учащиеся делают соответствующие пометки на листе партнера по паре. Один заранее выбранный ученик (успевающий в предмете) собирает все листы и выставляет в заранее подготовленную сводную ведомость отметки по ранее обозначенным критериям. Наиболее типичные неверные решения разбираются на доске учащимися, верно решившими пример. По этому же алогритму работы проводятся и последующие 2 самостоятельных работы.

Самостоятельная работа №2

I вариант	II вариант
1.f(x)=(1+2x)(2x-1), f `(-2)-?	1.f(x)=(3-2x)(2x+3), f `(-2)-?
2. (x)=7+x , `(8)-?	2. (x)=3+ , `(4)-?
3. g(x)=4sinx, g `(- )-?	3. g(x)=2cosx, g `(- )-?
4. h(x)= , h `(-1)-?	4.h(x)= , h `(-1)-?

Варианты ответов

1	2	3	4
-16	17	16	-17
	2	-	1
-2		-	2
3	1	-1	-3

Самостоятельная работа №3

I вариант	II вариант
f(x)=(2x+3)¹², f'(-2)-?	f(x)=(5+6x)¹⁰, f'(-1)-?
f(x)= , D(f)-?	f(x)= , D(f)-?
f(x)=x+1/x+2, g(x)=√x f(g(x))-? g(f(x))-?	f(x)=x/x-1, g(x)=√x f(g(x))-? g(f(x))-?

Варианты ответов

1	2	3	4
-52	-60	30	-24
(-∞;-7)U(-7;-5)U(5,+∞)	(-5;5)	(-∞;3)U(3;+∞)	(-5;5) x≠7
,	,	,	,

«Повторим геометрический смысл производной». На интерактивной доске появляются задания. Один ученик решает на интерактивной доске, двое – на боковых досках (все решают один пример).

Геометрический смысл производной

1) в какой точке параболы у = +3x -1 касательная наклонена к оси абсцисс под углом ?

2) найти тангенс угла наклона касательной у = 2 cos 3x в точке = .

3) найти тангенс угла наклона касательной к графику функции f(x)=2x³-5x в точке М(2;6).

4) какой угол с осью ОХ образует касательная к графику функции у = ctg 2x в точке с абсциссой x = -

5) при каком значении а прямая у = - 10x +a является касательной к графику функции

у = 3 - 4x -2?

6) при каком значении b прямая у=3x+b, является касательной к графику у = 2 - 5x +1?

7) какой угол образует с направлением оси ОХ касательная к графику функции

f(x)= (х-3) ?, проведенная в точке х=3.

«Повторим механический смысл производной». На интерактивной доске появляются задания. Один ученик решает на интерактивной доске, двое – на боковых досках, все решают один пример.

Механический смысл производной

Материальная точка движется по закону S(t)=3t²+4cos(0,5 t). Найдите скорость материальной точки в момент времени t=2с.

Найти скорость точки, движущейся прямолинейно по закону x(t)=2t³+t²-4 в момент времени t=4с.

4) Подведение итогов урока и задание на дом

Все учащиеся в процессе урока получали оценки, отмечаемые в сводной ведомости. В итоге урока каждому учащемуся выводится оценка как среднее арифметическое из всех полученных им за урок оценок. После этого объявляются оценки учащихся.