2.04.20. 8Б геометрия
Тема: Свойства серединного перпендикуляра
Цель: сформировать представление о серединном перпендикуляре к отрезку и
его свойствах.
1. Организационный момент
Конспектируем урок, учим основные понятия и теоремы.
2. Актуализация
ПРОВЕРЯЕТСЯ.
1.Письменно ответьте на вопросы.
1.1.Свойство любой точки биссектрисы неразвернутого угла?
1.2. Сформулируйте обратную теорему о свойстве биссектрисы угла.
1.3.Сколько биссектрис можно провести в треугольнике?
1.4.Что вы заметили, когда провели три биссектрисы в треугольнике?
1.5.Что называют серединой отрезка?
1.6.Сформулируйте определение перпендикулярных прямых.
2. Сделать № 677 и № 678
3. Новые знания
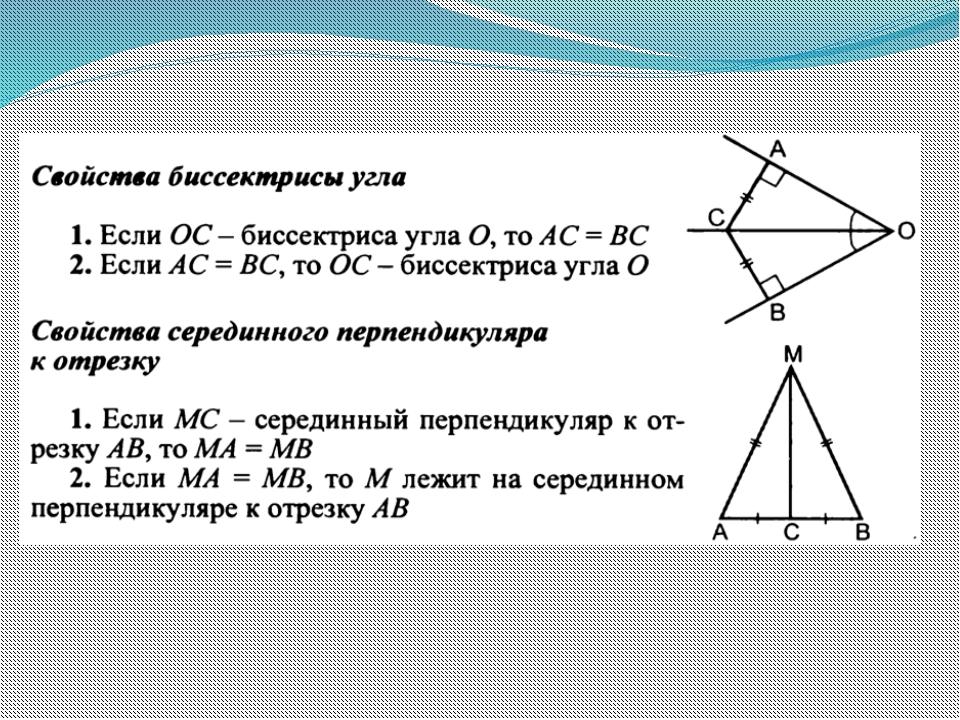
Рассмотрим свойства серединного перпендикуляра. Начнем со свойства серединного перпендикуляра к отрезку.
https://www.youtube.com/watch?v=K8cPYH_HWtI 8 класс, 36 урок, Свойства серединного перпендикуляра к отрезку
https://yandex.ru/video/preview/?filmId=17761247194602755741&text=свойства+серединного+перпендикуляра
Теорема.
(Свойство серединного перпендикуляра к отрезку).
I) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов
Д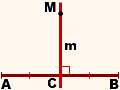 ано:
ано:
AB- отрезок, C — середина AB,
m — серединный перпендикуляр к AB,
M∈m.
Доказать: AM=BM.
Д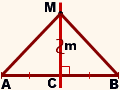 оказательство:
оказательство:
1. Если точка M совпадает с точкой C.
Так как AC=BC по условию, то и AM=BM.
2. Если точка M не совпадает с точкой C.
Рассмотрим треугольники ACM и BCM
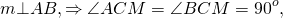
то есть треугольники ACM и BCM — прямоугольные.
AC=BC (по условию), CM — общий катет.
Следовательно, ∆ ACM=∆ BCM (по двум катетам).
Из равенства треугольников следует равенство соответствующих сторон: AM=BM.
Что и требовалось доказать.
Теорема обратная
Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Дано: AB — отрезок, C — середина AB,
m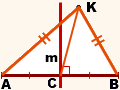 — серединный перпендикуляр к AB,
— серединный перпендикуляр к AB,
AK=BK.
Доказать: K∈m.
Доказательство:
Так как AK=BK (по условию), то треугольник AKB — равнобедренный с основанием AB (по определению). Так как C — середина AB, то KC — медиана треугольника AKB.
По свойству равнобедренного треугольника медиана, проведенная к основанию, является также его высотой, то есть
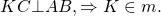
Что и требовалось доказать.
Вывод:
Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.
Теорема обратная (еще одно доказательство)
Каждая точка, равноудаленная от концов отрезка, лежит на серединном
перпендикуляре к этому отрезку.
Задан отрезок АВ, серединный перпендикуляр к нему р, точка М, равноудаленная от концов отрезка. Доказать, что точка М лежит на серединном перпендикуляре к отрезку (рис.).
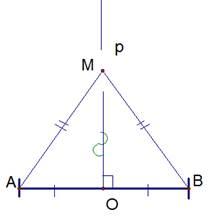 Иллюстрация к теореме
Иллюстрация к теореме
Доказательство:
Рассмотрим треугольник 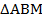 . Он равнобедренный, так как
. Он равнобедренный, так как 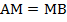 по условию. Рассмотрим медиану треугольника: точка О – середина основания АВ, ОМ – медиана. Согласно свойству равнобедренного треугольника, медиана, проведенная к его основанию, является одновременно высотой и биссектрисой. Отсюда следует, что
по условию. Рассмотрим медиану треугольника: точка О – середина основания АВ, ОМ – медиана. Согласно свойству равнобедренного треугольника, медиана, проведенная к его основанию, является одновременно высотой и биссектрисой. Отсюда следует, что 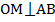 . Но прямая р также перпендикулярна АВ. Мы знаем, что в точку О можно провести единственный перпендикуляр к отрезку АВ, значит прямые ОМ и р совпадают, отсюда следует, что точка М принадлежит прямой р, что и требовалось доказать.
. Но прямая р также перпендикулярна АВ. Мы знаем, что в точку О можно провести единственный перпендикуляр к отрезку АВ, значит прямые ОМ и р совпадают, отсюда следует, что точка М принадлежит прямой р, что и требовалось доказать.
Рассмотрите пример решения задач.
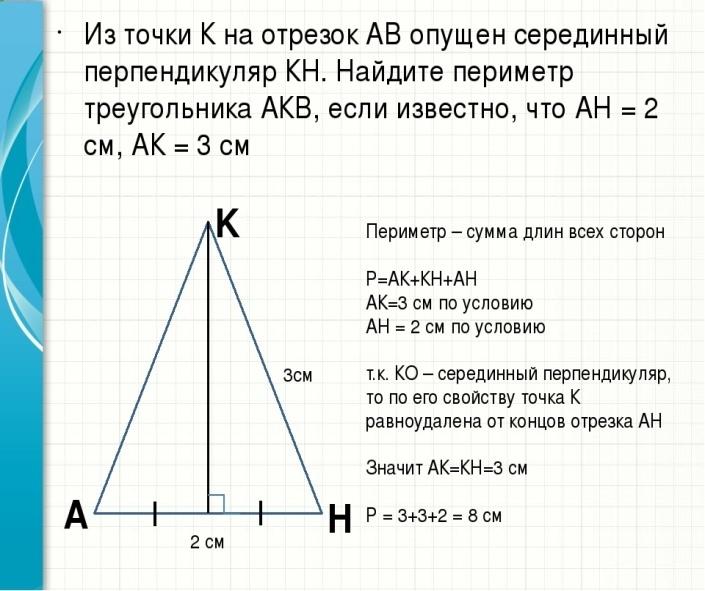
ПРОВЕРЯЕТСЯ
Выполнить построение и письменно доказать справедливость данного построения.
https://www.youtube.com/watch?v=ZLBTMihY4CM Построение середины отрезка
4. Домашняя работа
1. п.75, учим теорему и два следствия.
2. № 679 и № 680
3. Заполнить таблицу
| Тема занятия | Мои действия на занятии (слушал, выполнял эксперимент, общался...) | Я на занятии научился, узнал.. (оценивать свои действия, приобретать знания caмостоятельно и т.д.) | В чем ценность занятия для меня? | Что вызвало затруднения и почему? | Свою работу я оценил бы на оценку ..., потому что ... | Класс (учитель) выставил мне за работу оценку ... | Меня порадовало (огорчило) |





 ано:
ано: оказательство:
оказательство: — серединный перпендикуляр к AB,
— серединный перпендикуляр к AB, Иллюстрация к теореме
Иллюстрация к теореме



















