7 класс. ВПР по математике. Сборник задач тп 17.

1.  Задумали трёхзначное число, последняя цифра которого не равна нулю. Из него вычли трёхзначное число, записанное теми же цифрами в обратном порядке. Получили число 792. Найдите все числа, обладающие таким свойством.

Ответ: 901, 911, 921, 931, 941, 951, 961, 971, 981 или 991.

2.  Задумали трёхзначное число, все цифры которого различны и первая цифра которого четная. Из него вычли трехзначное число, записанное теми же цифрами в обратном порядке. Получили число 495. Найдите сумму наименьшего и наибольшего чисел, удовлетворяющих таким условиям.

Ответ: 1514.

3.  Трехзначное число, сложили с числом, записанным теми же цифрами, но в обратном порядке. В сумме получилось число 685. Найдите сумму цифр исходного числа.

Ответ: 14.

4.  Олег написал на доске четырехзначное число, а потом стер первую и последнюю цифры. Позже Олег захотел снова записать это число, но забыл стертые цифры. Единственное, что он помнит  — его число было кратно 15. Какое число могло быть написано на доске?

Ответ: 3150, 6150, 9150, 1155, 4155, 7155.

5.  Задумали трехзначное число, все цифры которого различны и вторая цифра которого четная. Из него вычли трехзначное число, записанное теми же цифрами в обратном порядке. Получили число 792. Найдите разность наибольшего и наименьшего чисел, удовлетворяющих таким условиям.

Ответ: 60.

6.  Задумали трехзначное число, все цифры которого различны и вторая цифра которого нечетная. Из него вычли трехзначное число, записанное теми же цифрами в обратном порядке. Получили число 693. Найдите сумму двух наибольших чисел, удовлетворяющих таким условиям.

Ответ: 1944.

7.  Задумали четырехзначное число, все цифры которого различны, вторая и третья цифры которого равны 3 и 8. Из него вычли четырехзначное число, записанное теми же цифрами в обратном порядке. Получили число 2547. Найдите сумму трех наименьших чисел, удовлетворяющих таким условиям.

Ответ: 17 147.

8.  Света выписывала на доску трехзначные числа с одним правилом: все они должны делиться на 4, но не делиться на 5. Найдите уменьшенную в 557 раз сумму всех чисел, удовлетворяющих условиям и не превышающих 145.

Ответ: 2.

9.  Леша собирал грибы. Набрав целую корзину, он принялся их пересчитывать, но постоянно сбивался. В итоге, Леша прекратил подсчет, поняв, что грибов не меньше, чем 640, и не больше, чем 655. Позже Леша понял, что собранными им грибы поровну раскладываются на 6 горстей. Какое наибольшее число грибов мог собрать Леша?

Ответ: 654 гриба.

10.  Задумали трехзначное число, все цифры которого различны и первая цифра которого нечетная. Из него вычли трехзначное число, записанное теми же цифрами в обратном порядке. Получили число 99. Найдите произведение наименьшего и наибольшего чисел, удовлетворяющих таким условиям.

Ответ: 295 356.

11.  Какое наименьшее число последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы получившаяся сумма была больше 496?

12.  Найдите две последние цифры числа 82**, если оно делится на 90.

13.  Из трёхзначного числа вычли число, записанное теми же цифрами, но в обратном порядке. На какие числа гарантированно делится полученная разность?

14.  Сумма цифр двузначного числа равна 12. Число, записанное теми же цифрами, но в обратном порядке, составляет от исходного числа. Найдите такое число.

15.  Если двузначное число разделить на число, записанное теми же цифрами, но в обратном порядке, то получится 4, а в остатке 3. Если же это число разделить на сумму его цифр, то в частном получится 8, а в остатке 7. Найдите это число.

16.  Сумма двух целых чисел равна 101, а разность их квадратов простое число. Найдите эти числа.

17.  Федя выписал на доску пятизначное число, кратное 12, а затем стер несколько цифр. На доске осталась запись  Какое число мог изначально написать Федя?

Ответ: 73 140, или 73 440, или 73 740, или 73 044, или  73 344, или 73 644, или 73 944, или 73 248, или 73 548, или 73 848.

18.  Игнат выписал на доску четырехзначное число, кратное 45, а затем стер несколько цифр. На доске осталась запись 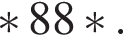 Какое число мог изначально написать Федя?

Ответ: 2880 или 6885.

19.  Марианна задумала четырехзначное число. Она сказала подругам, что оно кратно 30, его вторая цифра  — 2, и оно меньше 3500. Сколько чисел подходят под условия загадки Марианны?

Ответ: 10 чисел.

20.  У Фроси дома стоит сейф, на котором установлен четырехзначный кодовый замок. Код всегда был записан на бумажке, но со временем бумажка выцвела. Однако, Фрося была к такому готова и оставила себе ещё одну подсказку к открытию сейфа. В подсказке написано: «Код  — четырехзначное число, кратное 45, состоит из неповторяющихся цифр 0, 4, 2, 3.» Сейф автоматически блокируется навсегда, если ввести неверный код 4 раза. Хватит ли Фросе такого числа попыток, чтобы перебрать все варианты?

Ответ: нет, не хватит.

21.  В автобусах пассажирам выдают билеты с четырехзначным номером, начиная с 1000. На номере 3000 заканчивается рулетка с билетами, кондуктор открывает новую, где нумерация вновь идет сначала. Матрена собирает «счастливые» билеты. «Счастливыми» она называет те, число из первых двух цифр которых кратно 10, сумма последних двух цифр которых кратна 4, а весь номер кратен 3. Сколько всего «счастливых» билетов может собрать Матрена из одной рулетки?

Ответ: 17 билетов.

22.  Прасковья собирает карточки с изображениями животных. Всего карточек 1000, они пронумерованы от 1 до 1000. Прасковья раскладывает их в колоды по кратности номера  — колода кратных 2, колода кратных 3, колода кратных 5 и колода кратных 7. Сколько карточек из коллекции Прасковья может положить в каждую из колод?

Ответ: 4 карточки.