К началу учебного года! Готовые материалы для учителей на каждый урок со скидкой от 30%

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 18.05.2025 22:20

Мангаева Зульфира Хамидулловна

Учитель математики

35 лет

9 849

4 421

Подписчики

Подписки

Местоположение

Россия, Оренбургский район село имени 9 января

Специализация

Математика

Обо мне Блог Файлы Тесты Галерея Активность Награды

8 класс Геометрия 3.12.20 Практикум. Вычисление площадей.

Категория: Математика

02.12.2020 14:38

Проанализируйте задачи из конспекта, выполните задачи самостоятельно.

Просмотр содержимого документа
«8 класс Геометрия 3.12.20 Практикум. Вычисление площадей.»

3.12.2020г.

Геометрия

8 а/б класс. Ссылка на видеоурок https://youtu.be/lcEQemXqbf8

Тема урока: Площадь параллелограмма, треугольника и трапеции.

В учебнике эту тему можешь прочитать на странице 124, п. 51, п. 52, п. 53.

Ссылка на электронный учебник https://multiurok.ru/files/uchebnik-po-geometrii-8-klass.html. (Пройди по ссылке, прокрути вниз, нажми на кнопку «скачать»).

Рассмотрите примеры решений и решите задачи самостоятельно. Ответы на самостоятельные задачи внесите в таблицу, пришлите для проверки фото таблицы (вайбер или эл почта).

Таблица ответов:

№ задачи из конспекта	Ответ
Задача 1.
Задача 7.
Задача 8.
Задача 9.
Задача 10. (по желанию)
Задача 11. (по желанию)

Открой тетрадь и запиши число на полях и «Классная работа».

Ниже запиши тему урока.

Решение задач на нахождение площади параллелограмма, треугольника, трапеции.

На этом уроке мы будем находить площади изученных многоугольников. А также находить неизвестные величины, зная площадь и пользуясь формулой вычисления площади прямоугольника, квадрата, параллелограмма, трапеции и треугольника.

Устная задача.

Задача 1.

Решите устно, ответ запишите в таблицу.

Теперь рассмотрите следующую задачу:

Задача 2. Найдите площадь фигуры.

Решаем ее аналогично, то есть делим на условные сегменты, находим площадь каждого сегмента по отдельности, а затем складываем найденные площади.

Здесь мы уже используем формулу нахождения площади треугольника.

А теперь вспомните и подберите формулы ко всем многоугольникам для вычисления их площади:

1.Квадрат:

а) S=½a∙h

2.Прямоугольник:

б) S =a²

3.Параллелограмм:

в) S =a∙h

4.Трапеция:

г) S =a∙b

5.Треугольник:

д) S =½ (a + b)∙h

Запишите себе все формулы для нахождения площадей, выделите их. Они нам сегодня будут необходимы при решении задач на уроке.
Все задачи будем решать по следующему алгоритму.

Алгоритм решения задач на нахождение площади:

1. Записываем формулу
2. Выделяем неизвестный элемент
3. Делаем дополнительные построения
4. Рассматриваем треугольник
5. Находим неизвестный элемент, считаем.
6. Записываем ответ.

Рассмотрим задачу из учебника.

Задача 3.

№461. Смежные стороны параллелограмма равны 12 и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма.

Дано: ABCD- параллелограмм , AB=12 см, AD= 14 см, ∠BAD=30°

Найти:

Подумаем, какую формулу нужно применить, чтобы найти площадь?
Конечно, формулу площади параллелограмма, так как в условии дан параллелограмм.
Запишем ее: =a∙h

Еще нам понадобится свойство треугольника с углом в

Вспомните : катет, лежащий против угла в , равен половине гипотенузы.

Решение:

Дополнительные построения: BE - высота
∆ABE. ∠AEB=90°, ∠BAE=30°

BE = AB

BE = см

=AD∙BE

Ответ:

Вывод: Данную задачу мы решили с помощью свойства углов треугольника, свойства: катет, лежащий против угла в , равен половине гипотенузы и формулы площади параллелограмма.

Следующую задачу, разберите устно. Проанализируйте ход доказательства. И запомните вывод.

Задача 4.

№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырёхугольника равна половине произведения его диагоналей.

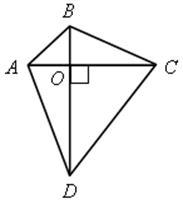
Дано: ABCD- выпуклый четырехугольник, AC, BD- диагонали AC BD

Доказать:

Подумайте, как можно найти площадь этой фигуры?

Аналогично задачам в начале урока - разбиением на треугольники. Посмотрите, на какие треугольники нужно разбить эту фигуру?

( )
Как найдем площадь ∆ABC?

(BO-высота ∆ABC, поэтому )

И ∆ADC?

(DO- высота ∆ADC, поэтому )

найдем по формуле: .

Доказательство:

Рассмотрим ∆ABC, BO-высота ∆ABC,
Рассмотрим ∆ADC, DO- высота ∆ADC

OD + OB = BD

Вывод: данную задачу мы решили с помощью разбиения фигуры, свойства площадей: метод разбиения на фигуры; формулы площади треугольника. Выяснили, что площадь четырёхугольника, у которого диагонали взаимно перпендикулярны, равна половине произведения его диагоналей.

Задача 5.

№476. Докажите, что площадь ромба равна половине произведения его диагоналей. Вычислите площадь ромба, если его диагонали равны 3,2 дм и 14 см.

Дано: ABCD- ромб

Доказать:

Вычислить: , где AC=3,2 дм, BD =14 см

Вспомним, что ромб –это параллелограм, у которого все стороны равны.

Нам пригодится свойство ромба: диагонали ромба взаимно перпендикулярны и делят его углы пополам.

В предыдущей задаче мы доказали, что площадь выпуклого четырёхугольника, у которого диагонали взаимно перпендикулярны, равна половине произведения его диагоналей.

Значит мы можем применить эту формулу к ромбу.

Решение:

1) ABCD- ромб, сл. AC BD , тогда (доказано в №478

2) AC=3,2 дм=32 см,

BD =14 см

Вывод: данную задачу мы решили с помощью свойства ромба и формулы площади выпуклого четырёхугольника, у которого диагонали взаимно перпендикулярны, доказанной номером ранее.

Рассмотрим еще одну задачу, теперь с трапецией.

Задача 6.
В трапеции АВСD АD – большее основание, D = 60. Биссектрисы углов С и D пересекаются в точке О, ОD = а, ВС = b, АD = с. Найдите площадь трапеции.

Дано:

ABCD- трапеция, ∠ADC=60°, CN-биссектриса ∠BCD, DF-биссектриса ∠ADC, CN∩DF=O, OD=a, BC=b, AD=c

Найти:

Запишем формулу площади трапеции

( ,)

Нам не хватает высоты

Поэтому достроим ее,причем, так, чтобы т.О ей принадлежала.

Теперь посмотрите и сравните ∆МСО и ∆KСО

(∆МСО=∆KСО)

Подумайте почему они равны?

(∠MCO=∠KCO, CO-общая, ∠MOC=∠KOC=90°-∠KCO)

Теперь посмотрите и сравните ∆ОРD ∆ОKD

(∆ОРD=∆ОKD)

Подумайте почему они равны?

(∠ODP=∠ODK, DO-общая, ∠POD=∠KOD=90°-∠OPD )

Из равенства ∆ следует:

ОМ = ОK и ОK = ОР, сл. ОМ = ОK= ОР

Так же не забываем про свойство прямоугольного треугольника: «Катет, лежащий против угла в ,равен половине гипотенузы.»

Решение:

∆МСО=∆KСО (∠MCO=∠KCO, CO-общая, ∠MOC=∠KOC=90°-∠KCO), следовательно ОМ = ОK.

∆ОРD=∆ОKD (∠ODP=∠ODK, DO-общая, ∠POD=∠KOD=90°-∠OPD ) следовательно ОK = ОР

ОМ = ОK и ОK = ОР, сл. ОМ = ОK= ОР

∆ОKD – прямоугольный, (∠ODK = ∠ = 30°), следовательно

6) MP = OM+OP =2OK

MP=a

Ответ:

Вывод: Данную задачу мы решили с помощью равенства треугольников, свойства: катет, лежащий против угла в ,равен половине гипотенузы и формулы площади трапеции.

Следующие задачи решите самостоятельно.
Задача 7. Стороны параллелограмма 10 см и 6 см, а угол между этими сторонами 150°. Найдите площадь этого параллелограмма.

Задача 8. №471 (из учебника)

Задача 9. № 481 (из учебника)

Рассмотрели различные задачи на нахождение площадей треугольника, параллелограмма и трапеции, доказали формулу нахождения площади ромба, посмотрели как площади треугольника, параллелограмма и трапеции используется в практических задачах.

Задачи для желающих.

Задача 10. Найдите углы параллелограмма, если его площадь равна 20 см², а высота, проведенная из вершины тупого угла, делит одну из сторон на отрезки 2 см и 8 см, считая от вершины острого угла.

Задача 11. Сравните площади параллелограмма и прямоугольника, если они имеют одинаковые основания и одинаковые периметры.

Если есть вопросы, задавайте. Если все понятно, переходите к самостоятельной работе в следующем файле.