Тема: «Рациональные уравнения»
Когда уравнение решаешь, дружок,
Ты должен найти у него корешок.
Значение буквы проверить несложно.
Поставь в уравнение его осторожно.
Коль верное равенство выйдет у вас
То корнем значенье зовите тотчас.
Цели урока:
Образовательные – закрепление и углубление материала в процессе решения различных упражнений по указанной теме; обеспечение сознательного усвоения материала;
Воспитательные – повышения активности учащихся; сформировать умение наблюдать закономерности.
Практические – сформировать умения применять алгебраический аппарат решения уравнений при решении задач.
Форма урока: деловая гора.
Оформление кабинета: опорные таблицы по теме. Свойства корней квадратного уравнения; таблица контрольных заданий для выявления знаний, умения. навыков учащихся, демонстрационные карточки для устного счета; различные виды тестов.
Ход урока.
I. Организационный момент. Учитель объявляет цель урок – подмечать закономерности, проводить рассуждения при решении уравнений;
Задачи – работать с различными видами по сложности тестами.
II. Проверка домашнего задания № 348 (1,2). Несколько учеников получили задания на дом – решить уравнения на пленке и через кодоскоп.
№ 348 (1,2)
 /
/
ОДЗ:  ,
, 


-

 и
и 
Число – 1 не удовлетворяет ОДЗ, значит корнем уравнения является число 2.
Ответ: 2
 /
/
ОДЗ:  ,
, 


 и
и 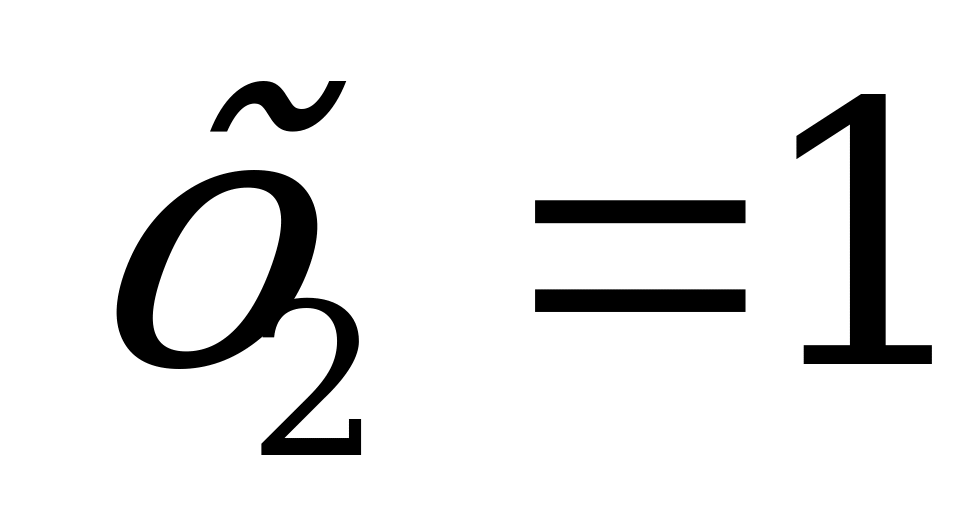
Ответ: 1
III. Выступление учителя.
Сегодня мы проведем урок в виде деловой игры. Продаются акции крупного предприятия. Вы покупаете и становитесь совладельцами. акции различны по стоимости.
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных и трансцендентных уравнений и неравенств. Поэтому при решении сегодня вы будете всё сводить к квадратным уравнениям.
Итак, разминка. Для выявления ЗУН учащихся выполняется самостоятельная работа по вариантам. У каждого ученика свой вариант, равный порядковому номеру в классном журнале.
Самостоятельная работа:

Историческая справка, выступает ученик.
Неполные квадратные уравнения и частные виды полных квадратных уравнений умели решать вавилоняне (примерно за 2 тыс. лет до н.э.). Некоторые виды квадратных уравнений решали древнегреческие математики, сводя их решение к геометрическим построениям. Правило решения квадратных уравнений, приведенных к виду 
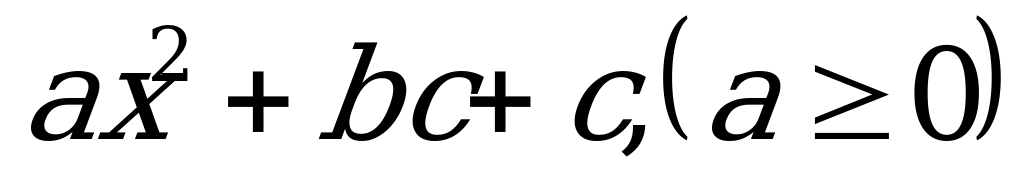 дал индийский ученый Брахмагупта (VII в.). Вывод формулы корней квадратного уравнения в общем виде имеется у Виета, однако он признавал, только положительные корни. Итальянские математики XVIв. учитывают помимо положительных и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
дал индийский ученый Брахмагупта (VII в.). Вывод формулы корней квадратного уравнения в общем виде имеется у Виета, однако он признавал, только положительные корни. Итальянские математики XVIв. учитывают помимо положительных и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
IV. Проверка знаний учащихся.
Продаются 6 акций, ребята решают у доски уравнения:
1. (-9;3)
(-9;3)
2. (-7;5)
(-7;5)
3. (0;5)
(0;5)
4.  (0;2
(0;2 )
)
5.  (-7)
(-7)
6.  (1;10)
(1;10)
В это же время 4 ученика выполняют за партой тестовые задания. Ещё два ученика работают с перфокартами.
| 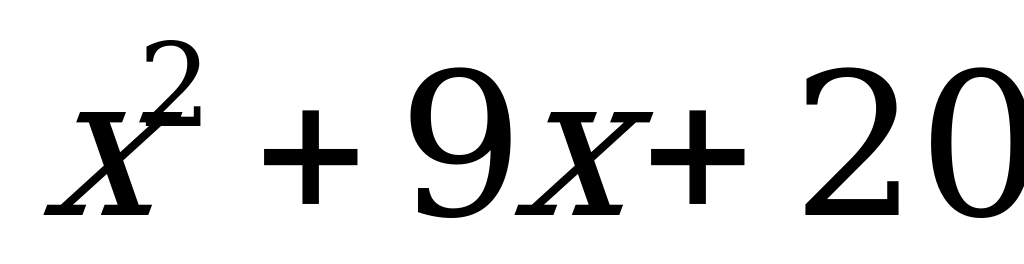
| -5;-4 | -5;-4 | 4;5 |
| 
| 12;-1 | 1;-12 | 3;4 |
| 
| 7;-8 | 8;7 | 2;28 |
И ещё два ученика играют в математическое домино, которое нужно собрать по принципу обычного домино; на каждой последующей карточке содержится ответ уравнения, написанного на предыдущей карточке. Первая карточка содержит слово «Начало», последней должна быть карточка со словом «Конец». После того, как цепочка собрана, можно перевернуть карточки и прочесть на обратной стороне поучительную поговорку:
«Ум без догадки гроша не стоит».
V. Устный опрос учащихся. Остальная часть класса работает с учителем устно. Продаются карточки для устного счета.
1. Решить уравнение 
А 1;4 В 1;5 С 4;5 Д 0
2. Решить уравнение 
А 1;6 В -1;-6 С 1;7 Д 0
3. Решить уравнение 
А 0 В 1;4 С -7;4 Д 1; 
4. Решите уравнение 
А 1;-3,5 В 0 С 1;-7 Д-1;7
5. Найти сумму корней 
А 2 В 4 С 1 Д 0,5
6. Найти произведение корней уравнения 
А -0,6 В0,6 С 0,4 Д -0,4
7. Определите знаки корней уравнения 
А 
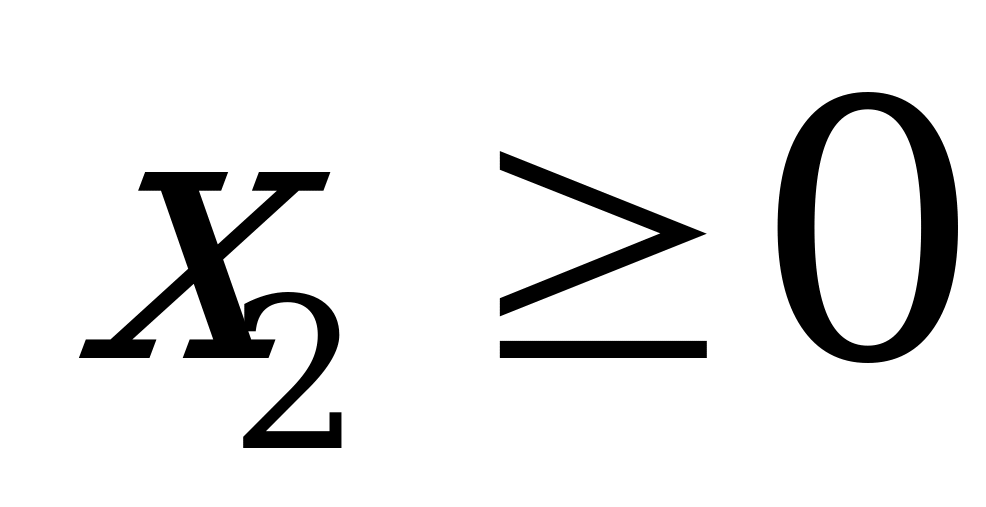 В
В 
 С
С 
 Д 0
Д 0
8. Разложите квадратный трехчлен на множители 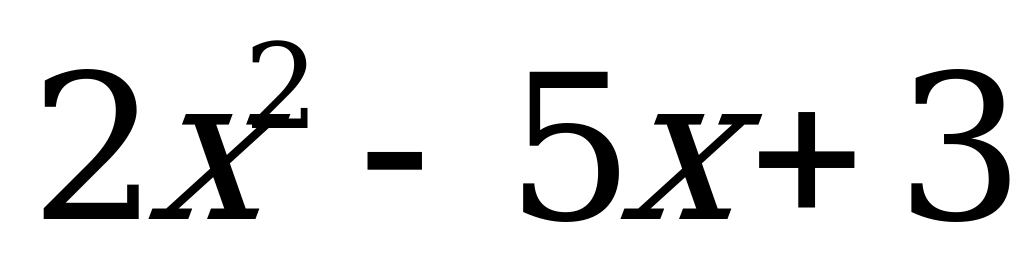
А 2(x-1)(x-1,5) B 2(x-1)(x-5) C (x-1)(2x-3) Д (x-1)(x-1,5)
VI. Закрепление темы.
Продаются акции карточки среднего уровня. №348(3) №355(задача)
 ОДЗ:
ОДЗ: 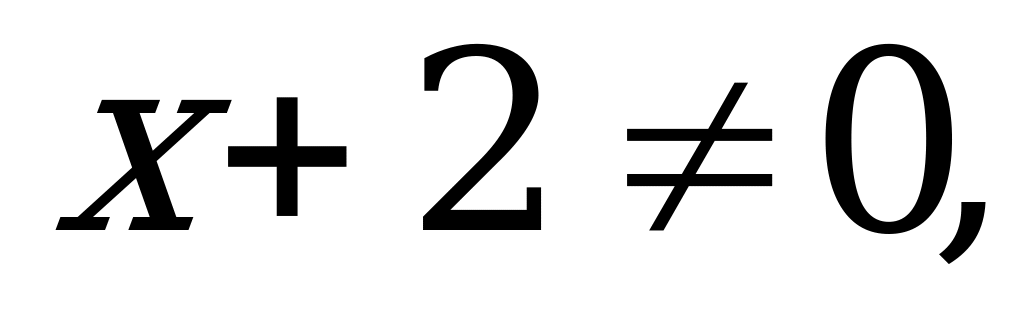
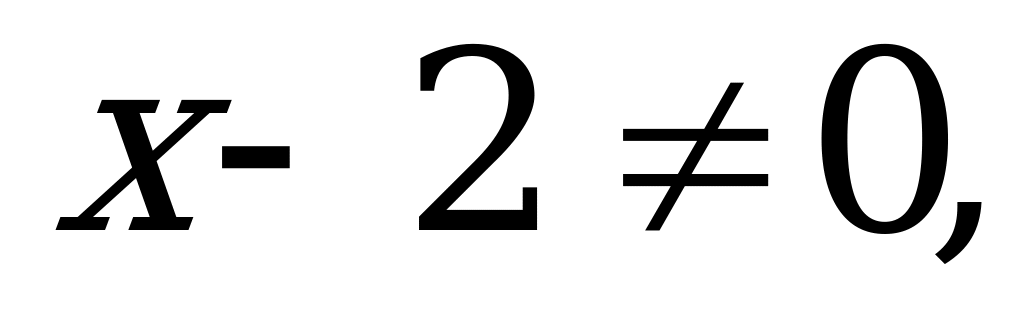




2x+(x-4)(x-2)=x+2, 

 , x=3 Ответ: 3
, x=3 Ответ: 3
№355 (задача по учебнику).
Катер проплыл 18 км по течению реки и 20 км против течения, затратив на весь путь 2ч. Найти скорость течения реки, если скорость катера в стоячей воде равна 20 км/ч.
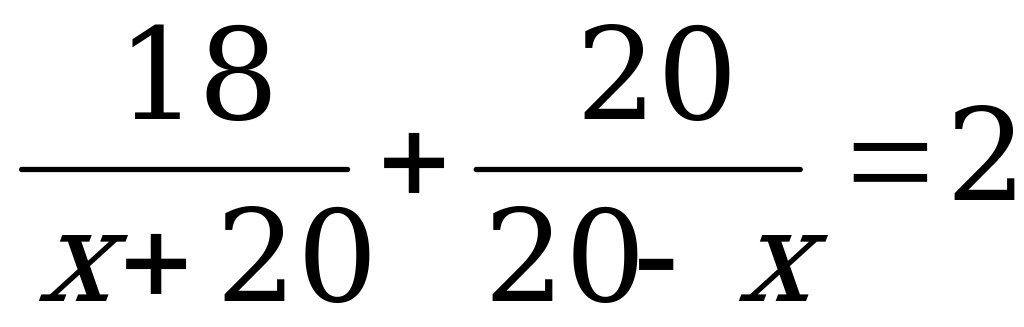
 Д=81.
Д=81.
Ответ: 4км/ч.
Задача – Швея ателье.
В одном ателье должны сшить 180 костюмов, а в другом -161 костюм. Первое ателье затратило на всю работу на 3 дня меньше, чем второе, т.к. изготавливало в день на 2 костюма больше. Сколько костюмов в день изготавливало каждое ателье?
за 1д общее число дней
I ателье. X+2 180  , на 3 дня меньше
, на 3 дня меньше
II ателье x 161 
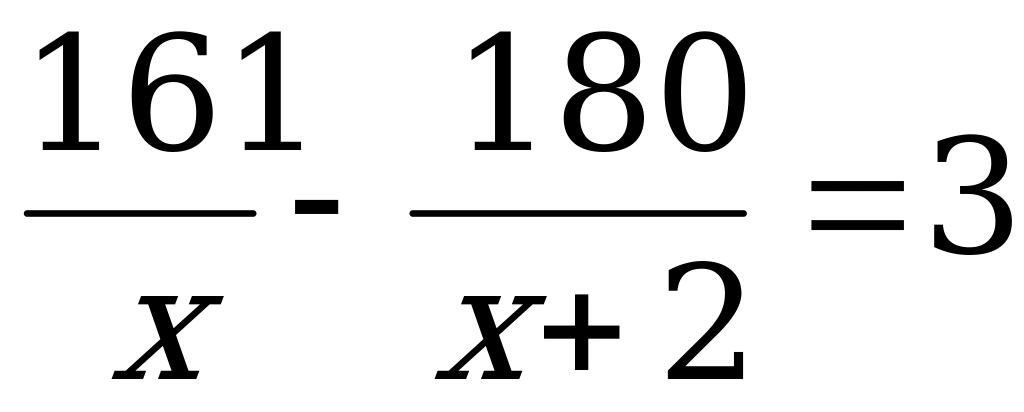 , 1)
, 1) 
 2)
2)  (костюмов).
(костюмов).
Д= 4489

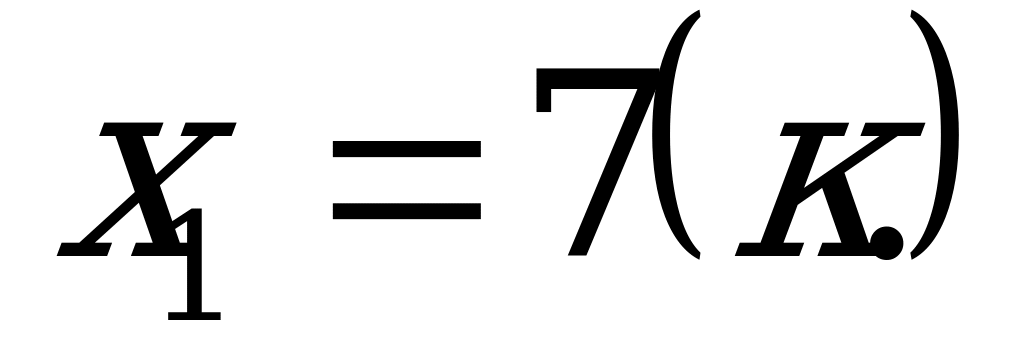
 (не удолвл. условию)
(не удолвл. условию)
Ответ: 9; 7 костюмов.
VII. Домашнее задание № 348 (4, 5, 6,)
VIII. Подвести итог урока.
Вопрос к классу – итак, при решении дробных уравнений удобно придерживаться каких правил?
Выставить оценки.

















