8-nji synp geometriýa 3-nji çärýek sapak ýazgy

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Güberçek köpburçluk
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Güberçek köpburçluklary öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Köpburçluk

3. Geçilen temany jemlemek:

1. Geometriýanyň meseleleriniň görnüşlerini aýdyň.

2. Gurmaga degişli meseläniň çözülişi näçe bölekden durýar?

3. Meseläniň analizi nähili geçirilýär?

4. Meseläniň derňewi nähili geçirilýär?

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1. Köpburçluklar barada umumy düşünje bermek.

2. Köpburçlugyň diagonallary we taraplary barada düşünje bermek

3. Güberçek köpburçluk barada öwretmek

Temany öwrenmek bilen okuwçylar bilmeli:

1. Köpburçluklar barada umumy düşünjeleri bilmeli

2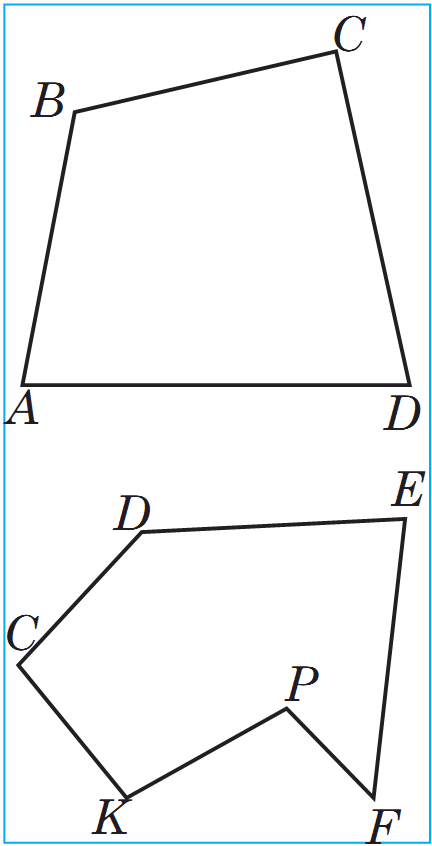 . Köpburçlugyň diagonallary we taraplary barada bilmeli

3. Güberçek köpburçlugyň häsiýetlerini bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1. Köpburçluklar barada umumy düşünjeleri bilmegi başarmaly

2. Köpburçlugyň diagonallary we taraplary tapmagy başarmaly

3. Güberçek köpburçlugyň burçlarynyň jeminiň formulasyny getirip çykarmagy başarmaly

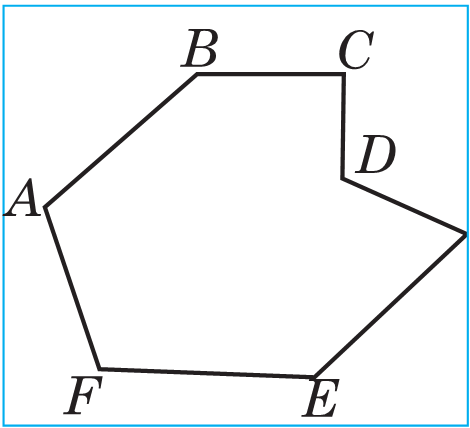
1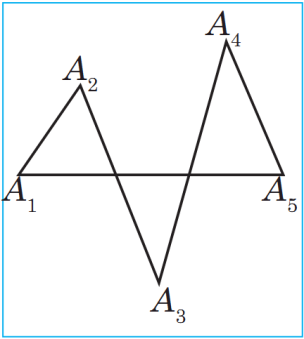 . Köpburçluk. Çatyk taraplary (AB we BC, BC we CD, ... FA we AB) bir göni çyzygyň üstünde ýatmaýan, çatyk däl taraplarynyň umumy nokady bolmadyk AB, BC, CD,...EF, FA kesimlerden düzülen geometrik figura köpburçluk diýilýär (sur.). A, B, C,... E, F nokatlara köpburçlugyň depeleri, AB, BC,... EF, FA kesimlere bolsa köpburçlugyň taraplary diýilýär.

Köpburçlukda taraplaryň iň az sany üçdür. Taraplaryň sany boýunça köpburçluga üçburçluk, dörtburçluk, bäşburçluk we ş.m. diýilýär, n sany tarapy bolan köpburçluga n burçluk diýilýär. Suratda ABCD dörtburçluk we CDEFPK altyburçluk şekillendirilendir şekillendirilen figura köpburçluk däldir. Sebäbi onuň çatyk däl A1A5 we A2A3, şeýle hem A3A4 we A1A5 taraplary kesişýärler.

Köpburçlugyň bir tarapyna degişli iki depesine goňşy depeler diýilýär. Köpburçlugyň goňşy däl islendik iki depesini birikdirýän kesime onuň diagonaly diýilýär.

I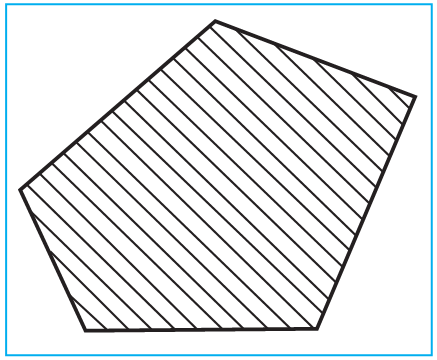 slendik köpburçluk tekizligi iki bölege bölýär. Olaryň b 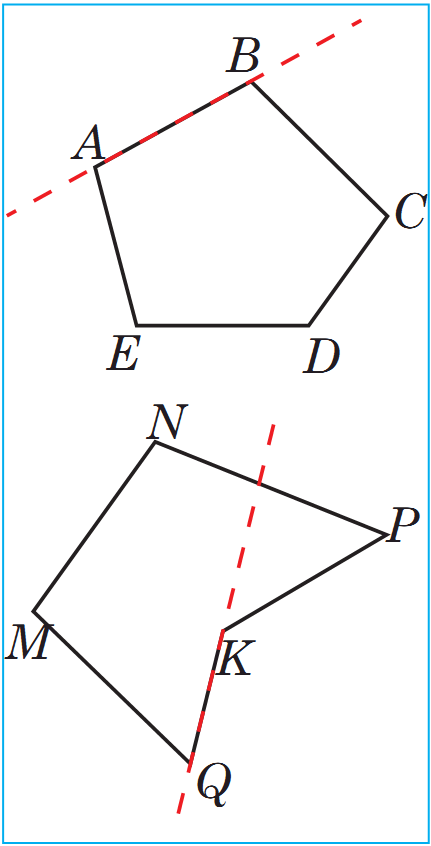irine köpburçlugyň içki ýaýlasy, beýlekisine daşky ýaýlasy diýilýär. suratda köpburçlugyň içki ýaýlasy ştrihlenendir.

Eger köpburçluk onuň islendik tarapy arkaly geçýän göni çyzykdan bir tarapda ýatýan bolsa, onda oňa güberçek köpburçluk diýilýär. Suratdaky ABCDE bäşburçluk güberçek köpburçlukdyr, MNPKQ bäşburçluk bolsa güberçek däldir.

G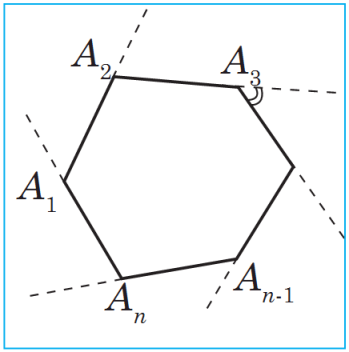 überçek köpburçlugyň depelerinde birleşýän taraplarynyň emele getirýän burçlaryna köpburçlugyň burçlary diýilýär. Güberçek köpburçlugyň berlen depesindäki içki burçuna çatyk bolan burça köpburçlugyň berlen depesindäki daşky burçy diýilýär (sur.).

Teorema. Güberçek n burçlugyň burçlarynyň jemi 180 (n – 2) deňdir.

S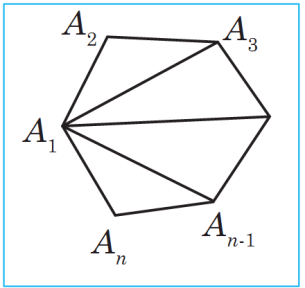 ubudy. Goý, A1A2...An n burçluk berlen bolsun (sur.). Onuň bir depesinden mümkin bolan ähli diagonallary geçireliň. Bu diagonallar berlen köpburçlugy n–2 sany üçburçluga böler (sur.). A1A2...An köpburçlugyň burçlarynyň jemi al nan üçburçluklaryň ählisiniň burçlarynyň jemi bilen gabat gelýär. Üç burçluklaryň her biriniň burçlarynyň jemi 180°-a deň, üçburçluklaryň sany bolsa n – 2 deňdir. Şoňa görä-de güberçek n burçlugyň burçlarynyň jemi 180°(n – 2) deň bolar.

5. Täze temany berkitmek:

140. (n–2)180⁰  1620⁰. n–21620⁰:180⁰, n–29, n11.

Jogaby: 11 burçy bar.

141. Güberçek n burçlugyň burçlary jemi 180(n–2)–ä deňdir.

a) n=5 üçin 180(5–2)=1803=540 bolar.

b) n=6 üçin 180(6–2)=1804=720 bolar.

ç) n=10 üçin 180(10–2)=1808=1440 bolar.

Jogaby: a) 540, b) 720, ç) 1440.

142.a) Goý, her bir burçy 90–a deň güberçek köpburçlugyň taraplarynyň sany n–e deň bolsun. Onda biz yazyp bileris:

180(n–2)=n90, bu ýerden 180n–360=90n, 180n–90n=360, 90n=360, n=360:90=4.

6. Öý işini tabşyrmak:

1. Köpburçluk diýip nämä aýdylýar? Güberçek köpburçluk näme?

2. Köpburçlugyň diagonaly diýlip nämä aýdylýar?

3. Güberçek köpburçlugyň burçlarynyň jeminiň formulasyny getirip çykaryň.

4. Güberçek dörtburçlugyň burçlarynyň jemi näçä deň?

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Gönükme çözmek.
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Güberçek köpburçluklary öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Güberçek köpburçluk

3. Geçilen temany jemlemek:

1. Geometriýanyň meseleleriniň görnüşlerini aýdyň.

2. Gurmaga degişli meseläniň çözülişi näçe bölekden durýar?

3. Meseläniň analizi nähili geçirilýär?

4. Meseläniň derňewi nähili geçirilýär?

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1. Köpburçluklar barada umumy düşünje bermek.

2. Köpburçlugyň diagonallary we taraplary barada düşünje bermek

3. Güberçek köpburçluk barada öwretmek

Temany öwrenmek bilen okuwçylar bilmeli:

1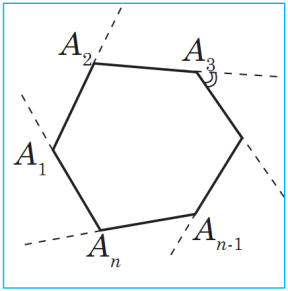 . Köpburçluklar barada umumy düşünjeleri bilmeli

2. Köpburçlugyň diagonallary we taraplary barada bilmeli

3. Güberçek köpburçlugyň häsiýetlerini bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1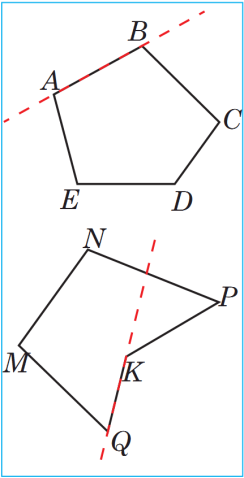 . Köpburçluklar barada umumy düşünjeleri bilmegi başarmaly

2. Köpburçlugyň diagonallary we taraplary tapmagy başarmaly

3. Güberçek köpburçlugyň burçlarynyň jeminiň formulasyny getirip çykarmagy başarmaly

E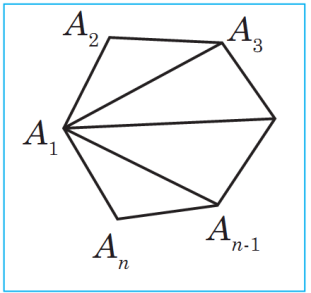 ger köpburçluk onuň islendik tarapy arkaly geçýän göni çyzykdan bir tarapda ýatýan bolsa, onda oňa güberçek köpburçluk diýilýär. Suratdaky ABCDE bäşburçluk güberçek köpburçlukdyr, MNPKQ bäşburçluk bolsa güberçek däldir.

Güberçek köpburçlugyň depelerinde birleşýän taraplarynyň emele getirýän burçlaryna köpburçlugyň burçlary diýilýär. Güberçek köpburçlugyň berlen depesindäki içki burçuna çatyk bolan burça köpburçlugyň berlen depesindäki daşky burçy diýilýär (sur.).

Teorema. Güberçek n burçlugyň burçlarynyň jemi 180 (n – 2) deňdir.

Subudy. Goý, A1A2...An n burçluk berlen bolsun (sur.). Onuň bir depesinden mümkin bolan ähli diagonallary geçireliň. Bu diagonallar berlen köpburçlugy n–2 sany üçburçluga böler (sur.). A1A2...An köpburçlugyň burçlarynyň jemi al nan üçburçluklaryň ählisiniň burçlarynyň jemi bilen gabat gelýär. Üç burçluklaryň her biriniň burçlarynyň jemi 180°-a deň, üçburçluklaryň sany bolsa n – 2 deňdir. Şoňa görä-de güberçek n burçlugyň burçlarynyň jemi 180°(n – 2) deň bolar.

5. Täze temany berkitmek:

142. b) a) bölümçedäkä meňzeş pikir ýöredip alýarys:

180(n–2)=n60, 180n–360=60n, 120n=360,

n=360:120, n=3.

Jogaby: n=3, deňtaraply üçburçluk.

ç) Öňki bölümçelerdäki meňzeşlikde ýazýarys:

180(n–2)=108n, 180n–360=180n, 72n=360, n=360:72, n=5.

Jogaby: n=5, dogry bäşburçluk.

d) 180(n–2)=120n, 180n–360=120n, 60n=360,

n=360:60, n=6.

Jogaby: n=6, dogry altyburçluk.

143. Bir tarapyny x bilen belgilesek, onda beýleki taraplary x–3, x–4 we x–5 bolar. P  x  x – 3  x – 4  x – 5  28, 4x  40,

x  10.

Jogaby: 10 sm, 7 sm, 6 sm, 5 sm.

144. Goý, güberçek dörtburçlugyň ähli deň bolan burçlarynyň ululygy  deň bolsun. Onda biz yazyp bileris:

180(4–2)=4, bu ýerden 360º=4, =90º.

Jogaby: =90º, n=4 dogry dörtburçlyk (kwadrat).

145. Güberçek sekizburçlugyň burçlarynyň jemi

180(8-2)=1806= 1080.

Güberçek dörtburçlugyň burçlarynyň jemi 360. Onda näçe köpdigini k bilen bellesek alarys:

.

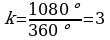Jogaby: 3 esse köp.

152. Güberçek dörtburçlugyň deň burçlary x bolsun. Onda güberçek dörtburçlugyň içki burçlarynyň jemi 360 deňligini hasaba alyp ýazýarys:

, , ,

, .

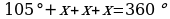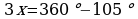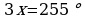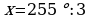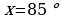6. Öý işini tabşyrmak:

1. Köpburçluk diýip nämä aýdylýar? Güberçek köpburçluk näme?

2. Köpburçlugyň diagonaly diýlip nämä aýdylýar?

3. Güberçek köpburçlugyň burçlarynyň jeminiň formulasyny getirip çykaryň.

4. Güberçek dörtburçlugyň burçlarynyň jemi näçä deň?

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Dörtburçluk
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Dörtburçluklary öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Güberçek köpburçluk

3. Geçilen temany jemlemek:

1. Köpburçluk diýip nämä aýdylýar? Güberçek köpburçluk näme?

2. Köpburçlugyň diagonaly diýlip nämä aýdylýar?

3. Güberçek köpburçlugyň burçlarynyň jeminiň formulasyny getirip çykaryň.

4. Güberçek dörtburçlugyň burçlarynyň jemi näçä deň?

4. Täze temany düşündirmek:

T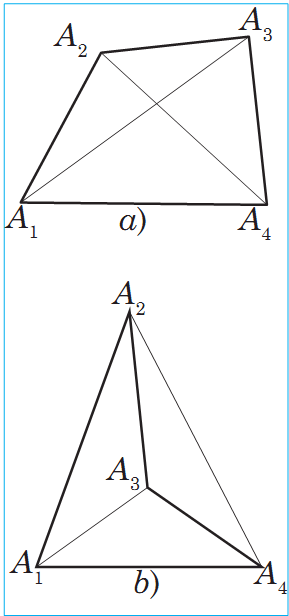 emany düşündirmegiň meýilnamasy:

1. Köpburçluklar barada umumy düşünje bermek.

2. Köpburçlugyň diagonallary we taraplary barada düşünje bermek

3. Dörtburçluk barada öwretmek

Temany öwrenmek bilen okuwçylar bilmeli:

1. Köpburçluklar barada umumy düşünjeleri bilmeli

2. Köpburçlugyň diagonallary we taraplary barada bilmeli

3. Dörtburçlugyň häsiýetlerini bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1. Köpburçluklar barada umumy düşünjeleri bilmegi başarmaly

2. Köpburçlugyň diagonallary we taraplary tapmagy başarmaly

3. Güberçek dörtburçlugyň burçlarynyň jemini tapmagy başarmaly

2. Dörtburçluk. Her bir dörtburçlugyň dört depesi, dört tarapy we iki diagonaly bardyr ( sur.). Dörtburçlugyň çatyk däl iki tarapyna garşylykly taraplary diýilýär. Dörtburçlugyň goňşy däl iki depesine garşylykly depeleri diýilýär.

Dörtburçluklar güberçek we güberçek däl bolup bilýärler.

a suratda güberçek, b suratda güberçek däl dörtburçluk şekillendirilendir. Güberçek dörtburçlugyň her bir diagonaly ony iki üçburçluga bölýär.

Güberçek n burçlugyň burçlarynyň jeminiň 180°(n – 2) deňdigi üçin, güberçek dörtburçlugyň burçlarynyň jemi

(4 – 2) ∙ 180° = 360°-a deň bolar.

5. Täze temany berkitmek:

146. Her bir burçy 165 bolan güberçek köpburçluk üçin

180(n–2)=165n, 180n–360=165n, 15n=360, .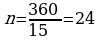

Jogaby: n=24, dogry ýigrimi dört burçluk.

147. Güberçek onburçlugyň we güberçek altyburçlugyň her biriniň burç­la­ry­nyň jemini tapýarys:

(10 – 2)180⁰  1440⁰, (6–2)180⁰  720⁰, 1440⁰ – 720⁰  720⁰.

Jogaby: 720⁰ köp.

148. Goý, bu güberçek köpburçlugyň taraplarynyň sany n bolsun. Onda

180(n–2)=1980 diýip ýazmak bolar. Bu ýerden n tapalyň

180n–360=1980, 180n=1980–360, 180n=1620,

n=1620:180, n=9.

Jogaby: n=9 dogry dokuzburçluk.

149. Meseläniň şertine görä 180(n–2)=2360 deňligi ýazmak bolar. Bu deňlikden n tapalyň 180n–360=720, 180n=360, n=360:180, n=2 .

Emma tarapy ikä deň bolan köpburçluk ýok.

Jogaby: Şeýle köpburçluk bolup bilmez.

6. Öý işini tabşyrmak:

1. Köpburçluk diýip nämä aýdylýar? Güberçek köpburçluk näme?

2. Köpburçlugyň diagonaly diýlip nämä aýdylýar?

3. Güberçek köpburçlugyň burçlarynyň jeminiň formulasyny getirip çykaryň.

4. Güberçek dörtburçlugyň burçlarynyň jemi näçä deň?

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Parallelogram we onuň häsiýetleri.
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Parallelogram we onuň häsiýetlerini öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Dörtburçluk

3. Geçilen temany jemlemek:

1. Köpburçluk diýip nämä aýdylýar? Güberçek köpburçluk näme?

2. Köpburçlugyň diagonaly diýlip nämä aýdylýar?

3. Güberçek köpburçlugyň burçlarynyň jeminiň formulasyny getirip çykaryň.

4. Güberçek dörtburçlugyň burçlarynyň jemi näçä deň?

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1. Köpburçluklar barada umumy düşünje bermek.

2. Parallelogram we onuň häsiýetleri barada düşünje bermek

3. Parallelogramyň diagonaly barada düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1. Köpburçluklar barada umumy düşünjeleri bilmeli

2. Parallelogram we onuň häsiýetleri barada düşünjeleri bilmeli

3. Parallelogramyň diagonaly barada düşünjeleri bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1. Köpburçluklar barada umumy düşünjeleri bilmegi başarmaly

2. Parallelogram we onuň häsiýetleri barada düşünjeleri bilmegi başarmaly

3. Parallelogramyň diagonaly barada düşünjelri bilmegi başarmaly

Garşylykly taraplary jübüt-jübütden parallel bolan dörtburçluga parallelogram diýilýär.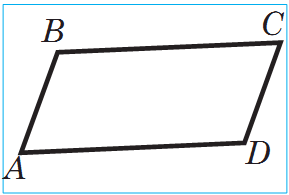

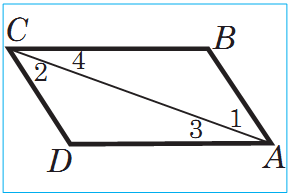
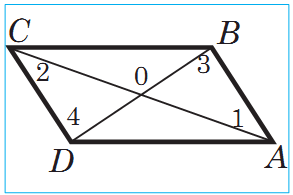
Suratda AB

1. Parallelogramyň diagonaly ony deň iki üçburçluga bölýär.

ABCD parallelograma seredeliň (sur.). AC diagonal bu parallelogramy ABC we ADC iki üçburçluga bölýär. Bir tarapy we oňa sepleşýän iki burçy boýunça ABC we ADC üçburçluklar deňdirler. Sebäbi AC tarap bu üçburçluklaryň ikisi üçin hem umumy, CD we AB parallel taraplar kesiji AC göni çyzyk bilen kesilende alnan atanak ýatan burçlar hökmünde E1 = E2, BC we AD parallel taraplar kesiji AC göni çyzyk bilen kesilende alnan atanak ýatan burçlar hökmünde E3 = E4.

2. Parallelogramyň garşylykly taraplary we garşylykly burçlary özara deňdirler.

ABC we ACD üçburçluklaryň deňliginden (sur.) olaryň degişli taraplarynyň we burçlarynyň deňligi, ýagny AB = CD, BC = AD we EB = ED alynýar.

E1 = E2 we E3 = E4 deňliklerden peýdalanyp alarys:

EA = E1 + E3 = E2 + E4 = EC. Diýmek, EA = EC.

3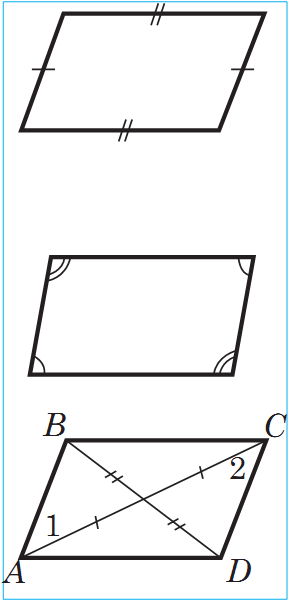 . Parallelogramyň diagonallary kesişme nokadynda deň ýarpa bölünýärler.

Goý, AC we BD ABCD parallelogramyň diagonallary we O olaryň kesişme nokady bolsun. AO=OC we BO=OD bolýandygyny subut edeliň (sur.). Munuň üçin garşylykly ýerleşen üçburçluklaryň haýsy bolsa-da bir jübütini, meselem, AOB we DOC üçburçluklary deňeşdirip göreliň. Bu üçburçluklarda parallelogramyň garşylykly taraplary bolany üçin AB = DC. DC we AB parallel göni çyzyklary AC göni çyzyk kesip ge çende emele gelýän atanak ýatan burçlar bolany üçin E1 =E2. DC we AB parallel göni çyzyklary BD göni çyzyk kesip geçende emele gelýän atanak ýatan burçlar bolany üçin E3 = E4.

Bu ýerden üçburçluklaryň deňliginiň ikinji nyşany (bir tarapy we oňa sepleşýän iki burçy) boýunça DOC üçburçluk AOB üçburçluga deňdir. Deň üçburçl uklarda bolsa deň burçlaryň garşysynda deň taraplar ýatýarlar. Diýmek, AO=OC we BO=OD. Suratda parallelogramyň ähli häsiýetleri görkezilendir.

5. Täze temany berkitmek:

Jogaby: 105; 85; 85; 85.

157. 2(CD+DE)=36, CD+DE=18;

CD+DE+CE=31, 18+CE=31,

CE=31-18, CE=13 sm

Jogaby: CE=13 sm.

158. 2(AB+BC)=54 sm,

AB+BC=27 sm.

a) BC=AB+5, AB+AB+5=27,

2AB=22, AB=11 sm,

BC=27-11=16;

b) BC-AB=7, BC=AB+7,

AB+AB+7=27, 2AB=20, AB=10 sm, BC=27-10=17;

ç) AB=BC:2, BC=2AB, AB+2AB=27, 3AB=27, AB=9 sm, BC=27-9=18;

Jogaby: a) 11 sm, 16 sm; b) 10 sm, 17 sm; ç) 9 sm, 18 sm.

6. Öý işini tabşyrmak:

1. Parallelogram diýlip nämä aýdylýar?

2. Parallelogramyň üç häsiýetini aýdyň we olary subut ediň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Gönükme çözmek.
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Parallelogram we onuň häsiýetlerini öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Parallelogram we onuň häsiýetleri

3. Geçilen temany jemlemek:

1. Köpburçluk diýip nämä aýdylýar? Güberçek köpburçluk näme?

2. Köpburçlugyň diagonaly diýlip nämä aýdylýar?

3. Güberçek köpburçlugyň burçlarynyň jeminiň formulasyny getirip çykaryň.

4. Güberçek dörtburçlugyň burçlarynyň jemi näçä deň?

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1. Köpburçluklar barada umumy düşünje bermek.

2. Parallelogram we onuň häsiýetleri barada düşünje bermek

3. Parallelogramyň diagonaly barada düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1. Köpburçluklar barada umumy düşünjeleri bilmeli

2. Parallelogram we onuň häsiýetleri barada düşünjeleri bilmeli

3. Parallelogramyň diagonaly barada düşünjeleri bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1. Köpburçluklar barada umumy düşünjeleri bilmegi başarmaly

2. Parallelogram we onuň häsiýetleri barada düşünjeleri bilmegi başarmaly

3. Parallelogramyň diagonaly barada düşünjelri bilmegi başarmaly

Garşylykly taraplary jübüt-jübütden parallel bolan dörtburçluga parallelogram diýilýär.

Suratda AB

1. Parallelogramyň diagonaly ony deň iki üçburçluga bölýär.

2. Parallelogramyň garşylykly taraplary we garşylykly burçlary özara deňdirler.3. Parallelogramyň diagonallary kesişme nokadynda deň ýarpa bölünýärler.

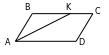
159. BAK=DAK, BK=15sm,

KC=6sm,BC||AD bolany üçin

BKA=DAK, bu ýerden

BAK=DAK=BKA. Diýmek

ABK deňýanly üçburçluk. AB=BK=15 sm, BC=BK+KC=15+6=21 sm. P=2(AB+BC)=2(15+21)=72 sm.

Jogaby: 72 sm.

5. Täze temany berkitmek:

160. P=42 sm, A=30º, BK=4,5 sm,

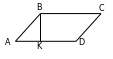göniburçly üçburçlukda 30º burçuň

gaşysyndaky katetiň gipotenuzanyň

ýarsyna deň bolýandygyndan alarys:

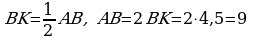sm,

P=2(AB+BC), 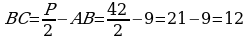sm.

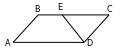Jogaby: AB=CD= 9sm, BC+AD=12 sm.

161. ADE=CDE, CD=8 sm,

BE=12sm, BC||AD bolany üçin

CED=ADE, bu ýerden

CED=ADE=CDE. Diýmek

DEC deňýanly üçburçluk. CE=CD=8 sm, BC=BE+EC=12+8=20 sm. P=2(AB+BC)=2(8+20)=56 sm.

Jogaby: 56 sm.

6. Öý işini tabşyrmak:

1. Parallelogram diýlip nämä aýdylýar?

2. Parallelogramyň üç häsiýetini aýdyň we olary subut ediň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Parallelogramyň nyşanlary
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Parallelogramyň nyşanlaryny öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Parallelogram we onuň häsiýetleri

3. Geçilen temany jemlemek:

1. Parallelogram diýlip nämä aýdylýar?

2. Parallelogramyň üç häsiýetini aýdyň we olary subut ediň.

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1 Parallelogramyň nyşanlary düşünje bermek.

2. Parallelogram we onuň häsiýetleri barada düşünje bermek

3. Parallelogramyň diagonaly barada düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1. Parallelogramyň nyşanlary barada umumy düşünjeleri bilmeli

2. Parallelogram we onuň häsiýetleri barada düşünjeleri bilmeli

3. Parallelogramyň diagonaly barada düşünjeleri bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1. Parallelogramyň nyşanlaryny subut etmegi başarmaly

2. Parallelogram we onuň häsiýetleri barada düşünjeleri bilmegi başarmaly

3. Parallelogramyň diagonaly barada düşünjelri bilmegi başarmaly

Parallelogramyň nyşanlary. Parallelogramyň üç nyşanyna seredeliň.

1. Eger dörtburçlugyň garşylykly iki tarapy deň we parallel bolsa, onda ol dörtburçluk parallelogramdyr.

G oý, ABCD dörtburçlukda AB = CD we ABCD bolsun, ABCD dörtburçlugyň parallelogramdygyny subut edeliň (sur.). Dörtburçlugyň AC diagonalyny geçireliň. AB we CD parallel göni çyzyklary AC göni çyzyk kesip geçende alnan atanak ýatan burçlar hökmünde E1 = E2. AB = CD, AC tarap umumy hem-de E1 = E2 bolany üçin, üçburçluklaryň deňliginiň birinji nyşany (iki tarapy we olaryň arasyndaky burçy) boýunça ABC we ADC üçburçluklar deňdirler. Bu üçburçluklaryň deňliginden 3 we 4 burçlaryň deňligi gelip çykýar, çünki olar deň üçburçluklarda deň taraplaryň garşysynda ýatýarlar. Emma 3 we 4 burçlar AD we BC göni çyzyklary AC göni çyzyk kesip geçende alnan atanak ýatan burçlardyr. Diýmek, AD we BC taraplar özara paralleldirler. Bu bolsa ABCD dörtburçlugyň parallelogramdygyny görkezýär.

2. Eger dörtburçlugyň garşylykly taraplary jübüt­jübütden deň bolsalar, onda ol dörtburçluk parallelogramdyr.

G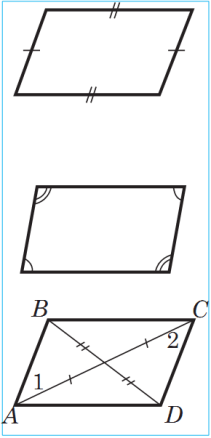 oý, ABCD dörtburçlukda AB=CD we AD=BC bolsun. AB tarapyň CD tarapa we AD tarapyň BC tarapa paralleldiklerini, ýagny ABCD dörtburçlugyň parallelogramdygyny subut edeliň (sur.). Bu dörtburçlugyň haýsy bolsa-da bir diagonalyny, meselem, AC diagonalyny geçireliň. AD = BC, AB = CD we AC tarap umumy bolany üçin, üçburçluklaryň deňliginiň üçünji nyşany (üç tarapy) boýunça ABC we ACD üçburçluklar deňdirler. Deň üçburçluklarda deň taraplaryň garşysynda deň burçlaryň ýatýanlygy üçin E1 =E2. 1 we 2 burçlar AB we CD göni çyzyklary AC göni çyzyk kesende alnan atanak ýatan burçlar bolany üçin ABCD. Şeýlelik bilen, AB = CD we ABCD bolany üçin, parallelogramyň birinji nyşanyna görä ABCD dörtburçluk parallelogramdyr.

3. Eger dörtburçlugyň diagonallary kesişseler we kesişme nokadynda deň ýarpa bölünýän bolsalar, onda ol dörtburçluk parallelogramdyr.

ABCD dörtburçlugyň AC we BD diagonallary O nokatda kesişýän we kesişme nokadynda deň ýarpa bölünýän bolsun (sur.). Bu dörtburçlugyň parallelogramdygyny subut edeliň. COD we AOB üçburçluklara seredeliň. Wertikal burçlar bolany üçin ECOD = EAOB. Şert boýunça CO = OA we BO = OD. Onda üçburçluklaryň deňliginiň birinji nyşany boýunça ∆COD = ∆AOB. Onda AB = CD we E1 = E2. 1 we 2 burçlaryň deňliginden ABCD gelip çykýar. AB we CD garşylykly taraplaryň deňligi we parallelligi üçin, parallelogramyň birinji nyşanyna görä ABCD dört burçluk parallelogramdyr.

5. Täze temany berkitmek:

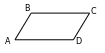164. a) D=95º, B=D=95º,

;

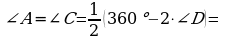
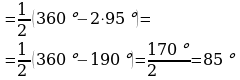Jogaby: B=D=95º, A=C=85º,

b) B-A=20º, B=A+20º, B+A=180º,

A+20º +A=180º, 2A=160º, A=80º, B=80º+20º=100º,

C=A=80º, D=B=100º;

Jogaby: C=A=80º, D=B=100º;

ç) A+C=142º, A=Cº, 2A=142º, A=71º, C=A=71º,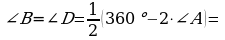

;

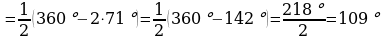Jogaby: C=A=71º, B=D=109º;

d) A=2B, A+B=180º, 2B+B=180º, 3B=180º, B=60º, D=B=60º, A=C=2B=260º=120º.

Jogaby: D=B=60º, A=C=120º.

6. Öý işini tabşyrmak:

1. Parallelogramyň birinji nyşanyny aýdyň we ony subut ediň.

2. Parallelogramyň ikinji nyşanyny aýdyň we ony subut ediň.

3. Parallelogramyň üçünji nyşanyny aýdyň we ony subut ediň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	3-nji ýazuw- barlag işi
Sapagyň maksady.
1) Bilim berijilik maksady:	Okuwçylaryň bilimini barlamak, pikirleniş endiklerini ösdürmek
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Ýazuw-barlag işi geçirilýän sapak
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Barlag iş depderleri

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak. 2. Okuwçylaryň sapaga taýýarlygyny barlamak.

3. Okuwçylaryň ünsüni sapaga gönükdirmek. 4. Syýasy wakalar bilen tanyşdyrmak.

2. Ýazuw-barlag işiniň mazmunyny düşündirmek.

a) Sag tarap b) Cep tarap

1.a) Güberçek sekizburçlugyň burçlarynyň jemini tapyň.

b) Güberçek dokuzburçlugyň burçlarynyň jemini tapyň.

2. a) Güberçek onburçlugyň ähli burçlary deň. Ol burçlary tapyň.

b) Güberçek altyburçlugyň ähli burçlary deň. Ol burçlary tapyň.

3. a) Eger güberçek dörtburçlugyň burçlarynyň biri 75° bolup, beýleki üç burçy bolsa özara deň bolsalar, onuň burçlaryny tapyň.

b) Eger güberçek dörtburçlugyň burçlarynyň biri 45° bolup, beýleki üç burçy bolsa özara deň bolsalar, onuň burçlaryny tapyň.

3. Okuwçylar tarapyndan ýazuw-barlag işiniň ýerine ýetirilmegi.

Çözlüşi

1. a) Güberçek n burçlugyň burçlary jemi 180(n–2)–ä deňdir. Onda n=8 üçin

180(8–2)=1806= 1080 bolar.

Jogaby: 1080.

b) Güberçek n burçlugyň burçlary jemi 180(n–2)–ä deňdir. Onda n=9 üçin

180(9–2)=1807= 1260 bolar.

Jogaby: 1260.

2. a) (n–2)180⁰  (10–2)180⁰  8180⁰  1440⁰. 1440⁰:10144⁰.

Jogaby: 144⁰.

b) (n–2)180⁰  (6–2)180⁰ 4180⁰  720⁰. 720⁰:6120⁰.

Jogaby: 120⁰.

3. a) Güberçek dörtburçlugyň deň burçlary x bolsun. Onda güberçek dörtburçlugyň içki burçlarynyň jemi 360 deňligini hasaba alyp ýazýarys:

, , ,

, .

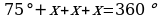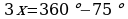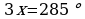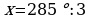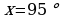b) Güberçek dörtburçlugyň deň burçlary x bolsun. Onda güberçek dörtburçlugyň içki burçlarynyň jemi 360 deňligini hasaba alyp ýazýarys:

, , ,

, .

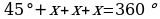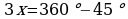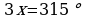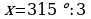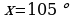4. Sapagy jemlemek, öý işini tabşyrmak.

Okuwçylaryň depderlerini toplap almak. Sapagy umumylaşdyryp jemlemek.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Gönüburçluk, romb, kwadrat we olaryň häsiýetleri
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Gönüburçluk, romb, kwadrat we olaryň häsiýetlerini öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Parallelogramyň nyşanlary

3. Geçilen temany jemlemek:

1. Parallelogramyň birinji nyşanyny aýdyň we ony subut ediň.

2. Parallelogramyň ikinji nyşanyny aýdyň we ony subut ediň.

3. Parallelogramyň üçünji nyşanyny aýdyň we ony subut ediň.

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1 Gönüburçluk barada düşünje bermek.

2. Romb we onuň häsiýetleri barada düşünje bermek

3. Kwadrat we onuň häsiýetleri barada düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1 Gönüburçluk barada düşünjeleri bilmeli

2. Romb we onuň häsiýetlerini bilmeli

3. Kwadrat we onuň häsiýetleri barada düşünjeleri bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1 Gönüburçluk barada düşünjeleri bilmegi başarmaly

2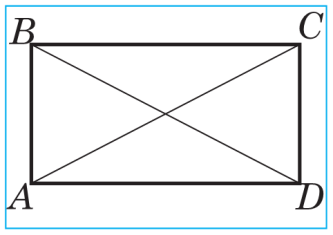 . Romb we onuň häsiýetleri barada bilmegi başarmaly

3. Kwadrat we onuň häsiýetleri barada düşünjeleri özleşdirmegi başarmaly

1. Gönüburçluk. Ähli burçlary göni burç bolan parallelograma gönüburçluk diýilýär. Gönüburçluk parallelogram bolany üçin, ol parallelogramyň ähli häsiýetlerine eýedir. Gönüburçlugyň garşylykly taraplary we burçlary özara deňdirler, onuň diagonallary bolan kesişme nokadynda deň ýarpa bölünýärler.

Bulardan başga-da gönüburçluk aşakdaky ýaly aýratyn häsiýete eýedir.

Gönüburçlugyň diagonallary deňdir.

ABCD gönüburçlugy alalyň we onuň AC hem-de BD diagonallaryny geçireliň. Diagonallaryň özara deňdiklerini subut edeliň (sur.). ABD we ACD üçburçluklary deňeşdireliň. Olaryň AD tarapy umumy we AB = DC. Diýmek, ABD we ACD gönüburçly üçburçluklar degişli katetleri deň bolandyklary üçin deňdirler. Onda ol gönüburçly üçburçluklaryň BD we AC gipotenuzalary hem deňdirler.

Ters tassyklamany (gönüburçlugyň nyşanyny) subut edeliň.

Eger parallelogramyň diagonallary deň bolsa, onda ol parallelogram gönüburçlukdyr.

Goý, ABCD parallelogramda AC we BD diagonallar deň bolsunlar (27­nji sur.). Onda ABD we DCA üçburçluklar üç tarapy boýunça (AB = DC, BD = AC, AD – umumy tarap) deňdirler. Bu ýerden EA = ED gelip çykýar. Parallelogramda garşylykly burçlaryň deňligi üçin EA = EC we EB = ED. Onda EA = EB = EC = ED. Parallelogram güberçek dörtburçluk bolany üçin

EA + EB + EC + ED = 360°. Diýmek, EA = EB = EC =

=ED = 90°. ABCD parallelogram gönüburçlukdyr.

Gönüburçluk görnüşli ýer bölegini ölçäp almaly, gönüburçluk görnüşli stoluň üstüniň, otagyň gapdal diwarynyň, surat ramkasynyň nähili takyklykda ýasalandygyny barlamaly bolanda gönüburçlugyň ýokardaky häsiýetinden peýdalanylýar.

Eger dörtburçlugyň garşylykly taraplary jübüt­jübütden deň bolup, onuň diagonallary hem deň bolsa, onda ol dörtburçluk gönüburçlukdyr. Eger dörtburçlugyň diagonallary deň bolmasa, onda ol gönüburçluk däldir we gönüburçluk almak üçin degişli düzedişleri girizmek zerurdyr.

5. Täze temany berkitmek:

163. B+C+D=286º,

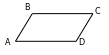2B+C=286º, 2B=286º-C,

2B+2C=360º,

286º-C+2C=360º,

C=360º-286º=74º,

2B=286º-C=286º-74º=212º, B=106º.

Jogaby: B=D=106º, A=C=74º.

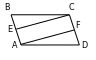
166. ABCD parallelogram we BE=DF.

BC=AD we B=D bolany üçin

EBF=FDA diýmek EC=AF; AB=CD

we BE=DF bolany üçin AE=CF,

ýagny AECF garşylykly taraplary deň

bolan dörtburçluk bolany üçin parallelogramdyr.

6. Öý işini tabşyrmak:

1. Gönüburçluk diýlip nämä aýdylýar?

2. Gönüburçlugyň häsiýetlerini aýdyň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Gönükme çözmek.
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Gönüburçluk, romb, kwadrat we olaryň häsiýetlerini öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Gönüburçluk, romb, kwadrat we olaryň häsiýetleri

3. Geçilen temany jemlemek:

1. Gönüburçluk diýlip nämä aýdylýar?

2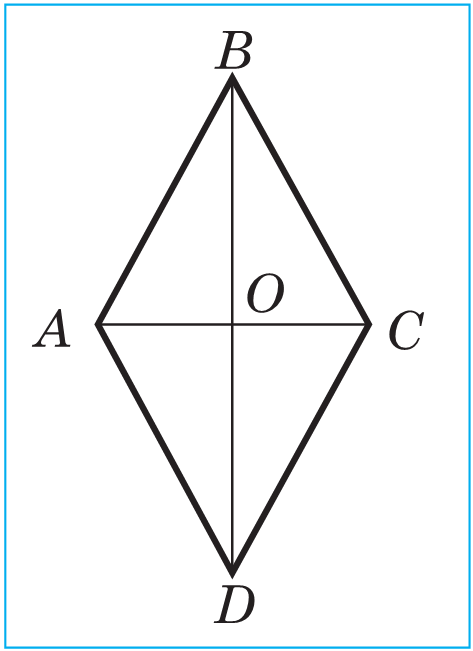 . Gönüburçlugyň häsiýetlerini aýdyň.

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1 Gönüburçluk barada düşünje bermek.

2. Romb we onuň häsiýetleri barada düşünje bermek

3. Kwadrat we onuň häsiýetleri barada düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1 Gönüburçluk barada düşünjeleri bilmeli

2. Romb we onuň häsiýetlerini bilmeli

3. Kwadrat we onuň häsiýetleri barada düşünjeleri bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1 Gönüburçluk barada düşünjeleri bilmegi başarmaly

2. Romb we onuň häsiýetleri barada bilmegi başarmaly

3. Kwadrat we onuň häsiýetleri barada düşünjeleri özleşdirmegi başarmaly

2. Romb we kwadrat. Ähli taraplary deň bolan parallelograma romb diýilýär.

Romb parallelogram bolany üçin, ol parallelogramyň ähli häsiýetlerine eýedir.

Rombuň diagonaly ony deň iki üçburçluga bölýär. Rombuň garşylykly burçlary we ähli taraplary deňdirler, onuň diagonallary bolsa kesişme nokadynda deň ýarpa bölünýärler.

Bulardan başga-da romb aşakdaky aýratyn häsiýete-de eýedir:

Rombuň diagonallary özara perpendikulýardyrlar we onuň burçlaryny deň ýarpa bölýärler.

A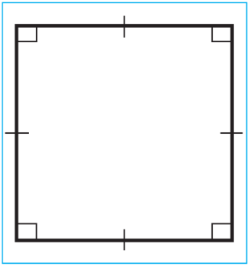 BCD romba seredeliň (sur.). AC=BD bolýandygyny we her bir diagonalyň degişli burçlary deň ýarpa bölýändigini, meselem, EBAC=EDAC bolýandygyny subut edeliň. Kesgitlenişi boýunça AB=AD, şoňa görä-de BAD deňýanly üçburçlukdyr. Romb parallelogram bolany üçin, onuň diagonallary O kesişme nokadynda ýarpa bölünýärler. Diýmek, AO kesim BAD deňýanly üçburçlugyň medianasydyr, beýikligidir hem-de bissektrisasydyr. Şoňa görä-de AC=BD we EBAC = ECAD. Teorema subut edildi.

Ä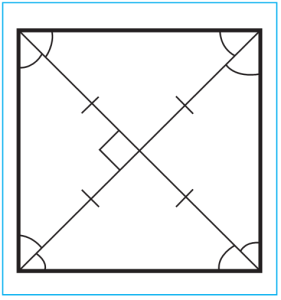 hli taraplary deň bolan gönüburçluga kwadrat diýilýär. Gönüburçlugyň parallelogramdygy üçin kwadrata hem ähli taraplary deň parallelogram, ýagny romb diýip bolar. Şoňa görä-de kwadrat gönüburçlugyň we rombuň ähli häsiýetlerine eýedir. Kwadratyň esasy häsiýetlerini belläp geçeliň.

1. Kwadratyň ähli burçlary gönüdir (sur.).

2. Kwadratyň diagonallary deňdir, özara perpendikulýardyrlar, kesişme nokady arkaly deň ýarpa bölünýärler. Kwadratyň diagonallary onuň burçlaryny deň ýarpa bölýär (sur.).

5. Täze temany berkitmek:

168. MO=7sm, MK=1,4 dm=14sm,

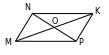NO=5sm, OP=50mm=5sm.

OK=MK-MO=14-7=7sm.

Diýmek NO=OP,MO=OK,

parallelogramlygyň 3-nji

nyşanyna görä ABCD dörtburçluk

parallelogramdyr

Jogaby: Hawa.

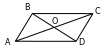169. AO=0,6dm=6sm, OB=3sm,

OC=BD=60mm=6sm. Diýmek AO=OC,

OB=OD, parallelogramlygyň 3-nji

nyşanyna görä ABCD dörtburçluk

parallelogramdyr

Jogaby: Hawa.

6. Öý işini tabşyrmak:

1. Romb diýlip nämä aýdylýar?

2. Rombuň häsiýetlerini aýdyň.

3. Kwadrat diýlip nämä aýdylýar?

4. Kwadratyň häsiýetlerini aýdyň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Trapesiýa
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Trapesiýany öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Gönüburçluk, romb, kwadrat we olaryň häsiýetleri

3. Geçilen temany jemlemek:

1. Romb diýlip nämä aýdylýar?

2. Rombuň häsiýetlerini aýdyň.

3. Kwadrat diýlip nämä aýdylýar?

4. Kwadratyň häsiýetlerini aýdyň.

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1 Trapesiýa barada düşünje bermek.

2. Trapesiýanyň gapdal taraplary barada düşünje bermek

3. Trapesiýanyň esaslary barada düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1 Trapesiýa barada düşünjeleri bilemeli

2. Trapesiýanyň gapdal taraplary barada bilmeli

3. Trapesiýanyň esaslary barada bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1 Trapesiýa barada düşünjeleri bilemegi başarmaly

2. Trapesiýanyň gapdal taraplaryny tapmagy başarmaly

3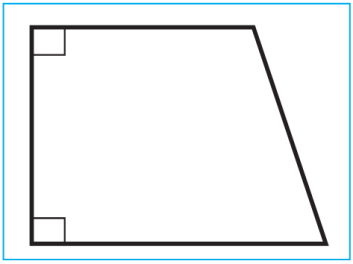 . Trapesiýanyň esaslary barada umumy düşünjeleri bilmegi başarmaly

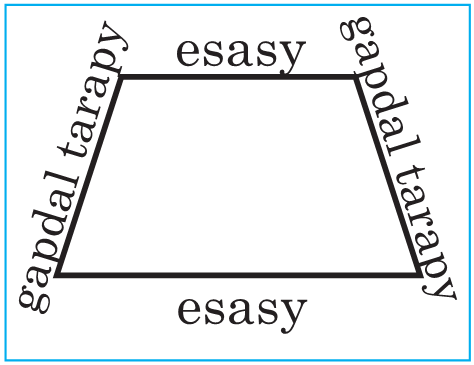
Trapesiýa. Iki tarapy parallel, beýleki iki tarapy bolsa parallel bolmadyk dörtburçluga trapesiýa diýilýär.

Trapesiýanyň parallel taraplaryna onuň esaslary, beýleki iki tarapyna bolsa gapdal taraplary diýilýär (sur.).

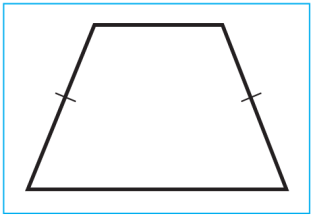
Eger trapesiýanyň gapdal taraplary deň bolsa, onda oňa deňýanly trapesiýa diýilýär (sur.).

Burçlarynyň biri göni burç bolan trapesiýa gönüburçly trapesiýa diýilýär (sur.).

5. Täze temany berkitmek:

175. A=63º, C=112º.

BE we CH beýiklikleri geçirip ABE

we DCH gönüburçly üçburçluklary

alarys.

ABE=180º-(A+AEB)=

=180º-(63º+90º)=180º-153º=27º,

B=ABE+CBE=27º+90º=117º,

DCH=C-BCH=112º-90º=22º,

D=180º-(DCH+DHC)=180º-(22º+90º)=180º-112º=68º.

Jogaby: D=117º, D=68º.

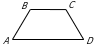176. ABCD-deňýanly trapesiýa, A=71º.

2A+2B=360º, A+B=180º,

B=180º-A=180º-71º=109º.

D=A=71º, C=B=109º.

Jogaby: D=A=71º, C=B=109º.

179. BE||CD, P_ABE=21sm, BC=7sm.

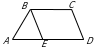BCDE parallelogram bolany üçin

BE=CD, BC=ED,

P_ABCD=AB+BC+CD+AD=

AB+BE+AE+2BC=21+27=

=21+14=35sm.

Jogaby: 35sm.

6. Öý işini tabşyrmak:

1. Romb diýlip nämä aýdylýar?

2. Rombuň häsiýetlerini aýdyň.

3. Kwadrat diýlip nämä aýdylýar?

4. Kwadratyň häsiýetlerini aýdyň.

5. Trapesiýa diýlip nämä aýdylýar?

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Gönükme çözmek.
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Falesiň teoremasyny öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Trapesiýa

3. Geçilen temany jemlemek:

1. Romb diýlip nämä aýdylýar?

2. Rombuň häsiýetlerini aýdyň.

3. Kwadrat diýlip nämä aýdylýar?

4. Kwadratyň häsiýetlerini aýdyň.

5. Trapesiýa diýlip nämä aýdylýar?

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1 Trapesiýa barada düşünje bermek.

2. Trapesiýanyň gapdal taraplary barada düşünje bermek

3. Falesiň teoremasy barada düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1 Trapesiýa barada düşünjeleri bilemeli

2. Trapesiýanyň gapdal taraplary barada bilmeli

3. Falesiň teoremasyny bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1 Trapesiýa barada düşünjeleri bilemegi başarmaly

2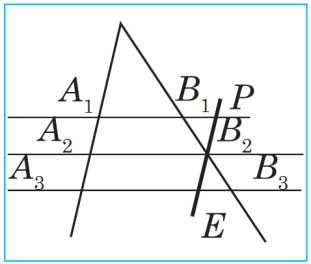 . Trapesiýanyň gapdal taraplaryny tapmagy başarmaly

3. Falesiň teoremasy barada umumy düşünjeleri bilmegi başarmaly

Falesiň teoremasy. Eger burçuň taraplaryny kesýän paralle l göni çyzyklar burçuň bir tarapynda deň kesimleri kesip alýan bolsalar, onda olar onuň beýleki tarapynda hem deň kesimleri kesip alarlar.

Subudy. Eger A₁A₂=A₂A₃ bolsa, onda B₁B₂=B₂B₃ bolýandygyny (sur.) subut edeliň.

B₂ nokat arkaly A₁A₃ göni çyzyga parallel EP göni çyzyk geçireliň.

Parallelogramyň häsiýeti boýunça

A₁A₂ = PB₂, A₂A₃ = B₂E. A₁A₂ = A₂A₃

bolýandygy üçin PB₂=B₂E. Üçburçluklaryň deňliginiň ikinji ny şanyna görä B₂B₁P we B₂B₃E üçburçluklar deňdirler. Subut edilişine görä olarda BP₂=B₂E. B₂ depedäki burçlar wertikal burçlar hökmünde deňdirler. EB₁PB₂=EB₂EB₃ (atanak ýatan burçlar).

Üçburçluklaryň deňliginden B₁B₂=B₂B₃ gelip çykýar. Teorema subut edildi.

Bellik. Falesiň teoremasynyň şertinde burçuň taraplaryna derek islendik iki göni çyzygy hem alyp bolar. Bu halda teorema aşakdaky ýaly aýdylýar.

Berlen iki göni çyzygy kesýän we göni çyzyklaryň birinde deň kesimleri kesip alýan parallel göni çyzyklar beýleki göni çyzykda hem deň kesimleri kesip alarlar.

5. Täze temany berkitmek:

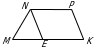
180. NE||PK, NME=70º, MNE=45º.

NEM=180º-70º-45º=65º,

NE||PK bolany üçin

NEM=PKM=65º,

MK||NP bolany üçin NPK=180º-PKM=180º-65º=115º,

ENP=PKM=65º, MNP=MNE+ENP=45º+65º=110º.

Jogaby: 70º, 110º, 65º, 115º.

181. ABCD-deňýanly trapesiýa,

A=60º, ACD=90º, AD=20sm,

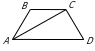BC=10 sm.

a) D=A=60º, CAD=90º-60º=30º,

BAC=A-CAD=60º-30º=30º , diýmek ,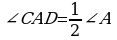

AC şöhle BAD burçuň bissektrisasy;

b) CAD=30º bolany üçin 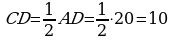, AB=CD=10, P=AB+BC+CD+AD=10+10+10+20=50 sm.

Jogaby: 50 sm.

6. Öý işini tabşyrmak:

1. Romb diýlip nämä aýdylýar?

2. Rombuň häsiýetlerini aýdyň.

3. Kwadrat diýlip nämä aýdylýar?

4. Kwadratyň häsiýetlerini aýdyň.

5. Trapesiýa diýlip nämä aýdylýar?

6. Falesiň teoremasyny aýdyň we burçuň taraplaryna derek islendik iki göni çyzygy alyp, bu teoremany subut ediň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Ok we merkezi simmetriýalar
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Ok we merkezi simmetriýalary öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Falesiň teoremasy

3. Geçilen temany jemlemek:

1. Romb diýlip nämä aýdylýar?

2. Rombuň häsiýetlerini aýdyň.

3. Kwadrat diýlip nämä aýdylýar?

4. Kwadratyň häsiýetlerini aýdyň.

5. Trapesiýa diýlip nämä aýdylýar?

6. Falesiň teoremasyny aýdyň we burçuň taraplaryna derek islendik iki göni çyzygy alyp, bu teoremany subut ediň.

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1 Simmetrik nokatlar barada düşünje bermek.

2. Simmetrik figuralar barada düşünje bermek

3. Ok we merkezi simmetriýalar barada düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1 Simmetrik nokatlar barada düşünjeleri bilmeli

2. Simmetrik figuralar barada düşünjeleri özleşdirip bilmeli

3. Ok we merkezi simmetriýalar barada bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1 Simmetrik nokatlar barada düşünjeleri bilmegi başarmaly

2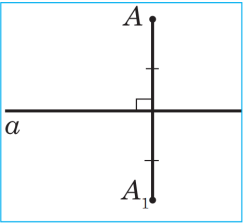 . Simmetrik figuralary bilmegi başarmaly

3. Ok we merkezi simmetriýalar barada bilmegi başarmaly

Eger a göni çyzyk AA₁ kesimiň ortasyndan geçse we oňa perpendikulýar bolsa, onda A we A₁ nokatlara a göni çyzyga görä simmetrik nokatlar diýilýär (sur.), a göni çyzygyň her bir nokady öz-özüne simmetrik hasap edilýär. Suratda M we M₁, K we K₁ nokatlar b göni çyzyga görä simmetrikdir, P nokat bolsa b göni çyzyga görä öz-özüne simmetrikdir.

E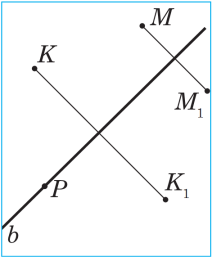 ger figuranyň her bir nokady üçin a göni çyzyga görä simmetrik nokat hem şol figura degişli bolsa, onda oňa a göni çyzyga görä simmetrik figura diýilýär, a göni çyzyga figuranyň simmetriýa oky diýilýär.

Ş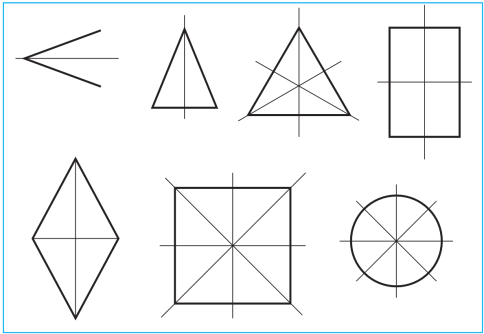 eýle ýagdaýda figuralara simmetriýa oky bar bolan figura diýilýär. Simmetriýa oky bolan figuralara mysallar getireliň (sur.). Ýazgyn däl burçuň bir simmetriýa oky bardyr. Ol simmetriýa oky burçuň bissektrisasynyň üstünden geçýän göni çyzykdyr. Deňýanly üçburçlugyň bir simmetriýa oky, deňtaraply üçburçlugyň bolsa üç simmetriýa oky bardyr. Kwadrat bolmadyk gönüburçlugyň we rombuň her haýsynyň iki simmetriýa oky bardyr. Töweregiň merkezinden geçýän islendik göni çyzyk onuň simmetriýa okudyr. Şoňa görä-de töweregiň tükeniksiz köp simmetriýa oklary bardyr.

Hiç bir simmetriýa oky bolmadyk figuralar hem bardyr. Şeýle figuralara gönüburçlukdan we rombdan tapawutly parallelogram, dürli taraply üçburçluk degişlidir.

5. Täze temany berkitmek:

195 Subudy. Goý, ABCD parallelogramyň

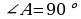bolsun, onda 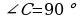bolar,

sebäbi garşylykly depedäki burç bolany

üçin. Parallelogramyň B=D garşy-

lykly depesindäki burçlary bolany üçin.

A+C=90+90=180 bolar, onda

B+D=180–a deňdir. B=D bolany üçin B=90 we D=90. Parallelogramyň burçlarynyň her biri 90–a deň, onda ol gönüburçluk. S.E.Ş.

197. Gönüburçlugyň diogrammalary kesişme nokadynda deň ýarpa bölünýärler. 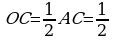. 14sm=7sm.

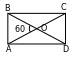AOB=COD wertikal burçlar bolany üçin.

Onda COD=60. COD–da OCD=ODC

we COD+OCD+ODC=180,

60+2OCD=180, 2OCD=180- 60,

2OCD=120, OCD=60. Diýmek 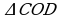deňtaraply

üçburçluk .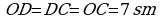

.

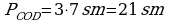6. Öý işini tabşyrmak:

1. Ok simmetriýasyny düşündiriň.

2. Merkezi simmetriýany düşündiriň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Gönükme çözmek.
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Ok we merkezi simmetriýalary öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Ok we merkezi simmetriýalar

3. Geçilen temany jemlemek:

1. Ok simmetriýasyny düşündiriň.

2. Merkezi simmetriýany düşündiriň.

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1 Simmetrik nokatlar barada düşünje bermek.

2. Simmetrik figuralar barada düşünje bermek

3. Ok we merkezi simmetriýalar barada düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1 Simmetrik nokatlar barada düşünjeleri bilmeli

2. Simmetrik figuralar barada düşünjeleri özleşdirip bilmeli

3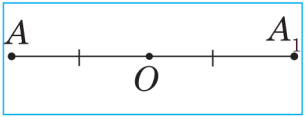 . Ok we merkezi simmetriýalar barada bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1 Simmetrik nokatlar barada düşünjeleri bilmegi başarmaly

2. Simmetrik figuralary bilmegi başarmaly

3. Ok we merkezi simmetriýalar barada bilmegi başarmaly

Hiç bir simmetriýa oky bolmadyk figuralar hem bardyr. Şeýle figuralara gönüburçlukdan we rombdan tapawutly parallelogram, dürli taraply üçburçluk degişlidir.

E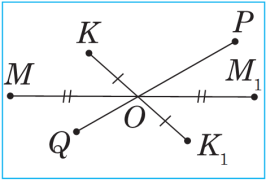 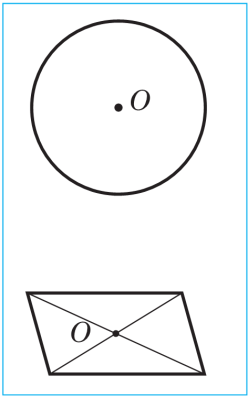ger O nokat AA₁ kesimiň ortasy bolsa, onda A we A₁ nokatlara O nokada görä simmetrik nokatlar diýilýär (sur.).

O nokat öz-özüne simmetrik nokat hasaplanylýar. Suratda M we M₁, K we K₁ nokatlar O nokada görä simmetrikdir, P we Q nokatlar bolsa O nokada görä simmetrik däldirler. Eger figuranyň her bir nokady üçin O nokada görä simmetrik nokat hem şol figura degişli bolsa, onda oňa O nokada görä simmetrik figura diýilýär. O nokada figuranyň simmetriýa merkezi diýilýär. Şeýle ýagdaýda figuranyň simmetriýa merkezi bar diýilýär.

Simmetriýa merkezi bolan figuralara mysallar getireliň. Töweregiň we parallelogramyň simmetriýa merkezi bardyr. Töweregiň simmetriýa merkezi töweregiň merkezidir. Parallelogramyň simmetriýa merkezi onuň diagonallarynyň kesişme nokadydyr. Töweregiň we parallelogramyň her biriniň diňe bir simmetriýa merkezi bardyr (sur.). Göni çyzygyň simmetriýa merkezi tükeniksiz köpdür. Göni çyzygyň islendik nokady onuň simmetriýa merkezi bolup biler. Simmetriýa merkezi bolmadyk figuralar hem bardyr. Mysal üçin, üçburçlugyň simmetriýa merkezi ýokdur.

B iziň daş-töweregimizi gurşap alan köp zatlaryň tekizlikdäki şekilleriniň simmetriýa merkezleri ýa-da simmetriýa oklary bardyr. Köp agaçlaryň ýapraklarynyň simmetriýa oky bardyr (sur.). Sungatda, binagärlikde, teh nikada, durmuşda biz simmetriýa bilen ýygy-ýygydan gabat gelýäris. Meselem, türkmen halylarynyň gölleriniň simmetriýa oky hem, simmetriýa merkezi hem bardyr (sur.).

5. Täze temany berkitmek:

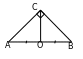198. Subudy. ABC–da 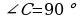, CO–me-

dianasy. Diýmek, 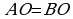berlişine görä,

emma gipotenuzanyň orta nokady ABC–yň

daşyndan çyzylan töweregiň merkezi bolýar,

onda CO=AO=BO. Bu ýerden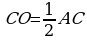

S.E.Ş.

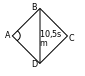199. AB=AD bolany üçin ,

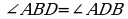ol burçlaryň her biri 60–a deňdirler.

Bu ýerden ABD–yň deňtaraplydygy gelip

çykýar. Diýmek, AB=AD=BD=10,5 sm. .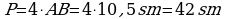

Jogaby: 42sm.

200. , ,

.

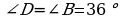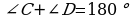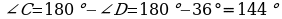
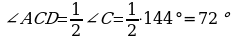Jogaby: 72.

6. Öý işini tabşyrmak:

1. Ok simmetriýasyny düşündiriň.

2. Merkezi simmetriýany düşündiriň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Gönükme çözmek.
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Ok we merkezi simmetriýalary öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Ok we merkezi simmetriýalar

3. Geçilen temany jemlemek:

1. Ok simmetriýasyny düşündiriň.

2. Merkezi simmetriýany düşündiriň.

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1 Simmetrik nokatlar barada düşünje bermek.

2. Simmetrik figuralar barada düşünje bermek

3. Ok we merkezi simmetriýalar barada düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1 Simmetrik nokatlar barada düşünjeleri bilmeli

2. Simmetrik figuralar barada düşünjeleri özleşdirip bilmeli

3. Ok we merkezi simmetriýalar barada bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1 Simmetrik nokatlar barada düşünjeleri bilmegi başarmaly

2. Simmetrik figuralary bilmegi başarmaly

3 . Ok we merkezi simmetriýalar barada bilmegi başarmaly

H iç bir simmetriýa oky bolmadyk figuralar hem bardyr. Şeýle figuralara gönüburçlukdan we rombdan tapawutly parallelogram, dürli taraply üçburçluk degişlidir.

E ger O nokat AA₁ kesimiň ortasy bolsa, onda A we A₁ nokatlara O nokada görä simmetrik nokatlar diýilýär (sur.).

O nokat öz-özüne simmetrik nokat hasaplanylýar. Suratda M we M₁, K we K₁ nokatlar O nokada görä simmetrikdir, P we Q nokatlar bolsa O nokada görä simmetrik däldirler. Eger figuranyň her bir nokady üçin O nokada görä simmetrik nokat hem şol figura degişli bolsa, onda oňa O nokada görä simmetrik figura diýilýär. O nokada figuranyň simmetriýa merkezi diýilýär. Şeýle ýagdaýda figuranyň simmetriýa merkezi bar diýilýär.

Simmetriýa merkezi bolan figuralara mysallar getireliň. Töweregiň we parallelogramyň simmetriýa merkezi bardyr. Töweregiň simmetriýa merkezi töweregiň merkezidir. Parallelogramyň simmetriýa merkezi onuň diagonallarynyň kesişme nokadydyr. Töweregiň we parallelogramyň her biriniň diňe bir simmetriýa merkezi bardyr (sur.). Göni çyzygyň simmetriýa merkezi tükeniksiz köpdür. Göni çyzygyň islendik nokady onuň simmetriýa merkezi bolup biler. Simmetriýa merkezi bolmadyk figuralar hem bardyr. Mysal üçin, üçburçlugyň simmetriýa merkezi ýokdur.

B iziň daş-töweregimizi gurşap alan köp zatlaryň tekizlikdäki şekilleriniň simmetriýa merkezleri ýa-da simmetriýa oklary bardyr. Köp agaçlaryň ýapraklarynyň simmetriýa oky bardyr (sur.). Sungatda, binagärlikde, teh nikada, durmuşda biz simmetriýa bilen ýygy-ýygydan gabat gelýäris. Meselem, türkmen halylarynyň gölleriniň simmetriýa oky hem, simmetriýa merkezi hem bardyr (sur.).

5. Täze temany berkitmek:

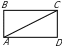
201. Görkezme. Meseläniň çözlüşi kateti we

oňa sepleşýän burçy boýunça gönüburçly

üçburçlugy gurmaga syrykdyrylýar.

Munuň şeýledigine göz ýetirmek üçin

meseläniň analizini geçireliň.

Goý, şeýle gönüburçlyk gurlan bolsun. AB tarap

we BAC burç berlen bolsun. Bu maglumatlar

boýunça BAC gönüburçly üçburçlygy gurup bolýar.

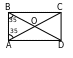
202. AC, BD gönüburçlugyň diogonallary.

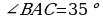berlen, onda

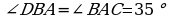bolar. Diýmek gözlenýän

BOA=180-(BAC+DBA)=180-70=110.

Jogaby: 110 we 70.

203. Görkezme. Meseläniň çözlüşi gapdal

taraplary we olaryň arasyndaky burçy bo­ýun­ça

deňýanly üçburçlugy gurmaga getirilýär.

AB  AD taraplary we BAD burçy boýunça

ABD deňýanly üçburçlugy gurup bolýar.

6. Öý işini tabşyrmak:

1. Ok simmetriýasyny düşündiriň.

2. Merkezi simmetriýany düşündiriň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	4-nji ýazuw- barlag işi
Sapagyň maksady.
1) Bilim berijilik maksady:	Okuwçylaryň bilimini barlamak, pikirleniş endiklerini ösdürmek
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Ýazuw-barlag işi geçirilýän sapak
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Barlag iş depderleri

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak. 2. Okuwçylaryň sapaga taýýarlygyny barlamak.

3. Okuwçylaryň ünsüni sapaga gönükdirmek. 4. Syýasy wakalar bilen tanyşdyrmak.

2. Ýazuw-barlag işiniň mazmunyny düşündirmek.

a) Sag tarap b) Cep tarap

1.a) Parallelogramyň üç burçunyň jemi 280°. Parallelogramyň burçlaryny tapyň.

b) a) Parallelogramyň üç burçunyň jemi 290°. Parallelogramyň burçlaryny tapyň.

2. a) ABCD dörtburçlugyň diagonallary O nokatda kesişýärler we AO = 0,8 dm, OB = 4 sm, OC = BD = 80 mm. Bu dörtburçluk parallelogrammy?

b) ABCD dörtburçlugyň diagonallary O nokatda kesişýärler we AO = 0,4 dm, OB = 2 sm, OC = BD = 40 mm. Bu dörtburçluk parallelogrammy?

3. a) Deňýanly trapesiýanyň burçlarynyň biri 70°. Trapesiýanyň beýleki burçlaryny tapyň.

b) Deňýanly trapesiýanyň burçlarynyň biri 60°. Trapesiýanyň beýleki burçlaryny tapyň.

3. Okuwçylar tarapyndan ýazuw-barlag işiniň ýerine ýetirilmegi.

Çözlüşi

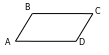1. a) B+C+D=280º,

2B+C=286º, 2B=280º-C,

2B+2C=360º,

280º-C+2C=360º,

C=360º-280º=80º,

2B=286º-C=280º-80º=200º, B=100º.

Jogaby: B=D=100º, A=C=80º.

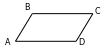b) B+C+D=290º,

2B+C=290º, 2B=290º-C,

2B+2C=360º,

290º-C+2C=360º,

C=360º-290º=70º,

2B=290º-C=290º-70º=220º, B=110º.

Jogaby: B=D=110º, A=C=70º.

2.a) AO=0,8dm=8sm, OB=4sm,

OC=BD=80mm=8sm. Diýmek AO=OC,

OB=OD, parallelogramlygyň 3-nji

nyşanyna görä ABCD dörtburçluk

parallelogramdyr

Jogaby: Hawa.

b) AO=0,4dm=4sm, OB=2sm,

OC=BD=40mm=4sm. Diýmek AO=OC,

OB=OD, parallelogramlygyň 3-nji

nyşanyna görä ABCD dörtburçluk

parallelogramdyr

Jogaby: Hawa.

3.a) ABCD-deňýanly trapesiýa, A=70º.

2A+2B=360º, A+B=180º,

B=180º-A=180º-70º=110º.

D=A=70º, C=B=110º.

Jogaby: D=A=70º, C=B=110º.

b) ABCD-deňýanly trapesiýa, A=60º.

2A+2B=360º, A+B=180º,

B=180º-A=180º-60º=120º.

D=A=60º, C=B=120º.

Jogaby: D=A=60º, C=B=120º.

4. Sapagy jemlemek, öý işini tabşyrmak.

Okuwçylaryň depderlerini toplap almak. Sapagy umumylaşdyryp jemlemek.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Köpburçlugyň meýdany hakynda düşünje
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Köpburçlugyň meýdany hakynda düşünjeleri öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

4-nji ýazuw- barlag işi

3. Geçilen temany jemlemek:

1. Ok simmetriýasyny düşündiriň.

2. Merkezi simmetriýany düşündiriň.

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1 Köpburçluklar barada düşünje bermek.

2. Köpburçlugyň meýdany barada düşünje bermek

3. Meýdanlaryň häsiýetleri hakynda düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1 Köpburçluklar barada düşünjeleri bilmeli

2. Köpburçlugyň meýdany barada bilmeli

3. Meýdanlaryň häsiýetleri hakynda düşünjeleri bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1 Köpburçluklar barada düşünjeleri bilmegi başarmaly

2. Köpburçlugyň meýdany barada bilmegi başarmaly

3. Meýdanlaryň häsiýetleri hakynda bilmegi başarmaly

Köpburçlugyň meýdany düşünjesi. Biz durmuşda geometrik figuralaryň meýdanlaryny ölçemek meselesine ýygy-ýygydan duş gelýäris. Meselem, gowaça meýdanynyň, sport meýdançasynyň, jaýyň polunyň, otagyň diwarlarynyň ýa-da penjireleriň meýdanlaryny kesgitlemeli bolýar.

Bilşimiz ýaly, kesimiň uzynlygyny ölçänimizde biz ony metr, santimetr, millimetr ýa-da uzynlygyň haýsy bolsa-da başga bir ölçeg birligi bilen deňeşdirýäris. Burçlary ölçänimizde biz burç ölçeg birliklerini – graduslary, minutlary peýdalanýarys.

Edil şuňa meňzeş geometrik figuralaryň meýdanlary ölçelende aýratyn ölçeg birlikleri peýdalanylyp, ol figuralaryň meýdanlary şol ölçeg birlikleri bilen deňeşdirilýär.

Köpburçlugyň tekizlikde eýeleýän böleginiň ululygyna onuň meýdany diýip aýtmak bolar. Saýlanylyp alnan ölçeg birligine görä meýdanlary ölçemeklik kesimleriň uzynlyklaryny ölçemeklik ýaly amala aşyrylýar. Eger kesimi ölçemegiň birligi hökmünde santimetr alnan bolsa, onda meýdan ölçemegiň birligi hökmünde tarapy 1 sm bolan kwadrat alynýar. Şeýle kwadrata – kwadrat santimetr diýilýär we sm² görnüşde belgilenilýär. Şuňa meňzeşlikde kwadrat metr (m²), kwadrat millimetr (mm²) ýaly ölçeg birlikleri kesgitlenendir. Meýdanlary ölçemegiň saýlanylyp alnan ölçeg birligine laýyklykda her bir köpburçlugyň meýdany käbir položitel san bilen aňladylýar. Bu san ölçeg birliginiň we onuň bölekleriniň näçesiniň berlen köpburçlukda ýerleşýändigini görkezýär.

Adatça, köpburçluk bilen baglanyşykly kesimleriň käbirleriniň uzynlyklary ölçenilýär, soňra bolsa kesgitlenilen formulalar boýunça köpburçlugyň meýdany hasaplanylýar. Bu formulalaryň getirilip çykarylyşy meýdanlaryň aşakdaky häsiýetlerine esaslanandyr.

1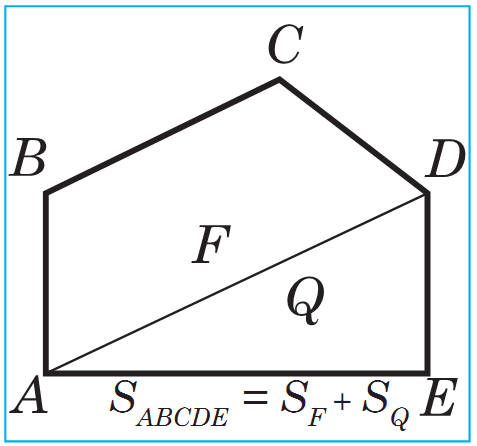 . Deň köpburçluklaryň deň meýdanlary bardyr.

Bu häsiýet, iki köpburçluk deň bolsa, onda olaryň her birinde ölçeg birliginiň we onuň bölekleriniň deň mukdarda ýerleşjekdigini görkezýär.

2. Eger köpburçluk käbir köpburçluklardan düzülen bolsa, onda onuň meýdany bu köpburçluklaryň meýdanlarynyň jemine deňdir.

S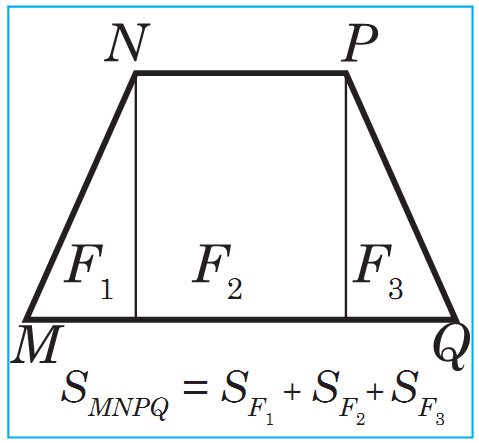 uratda şekillendirilen ABCDE bäşburçlugyň meýdany ABCD trapesiýanyň we ADE üçburçlugyň meýdanlarynyň jemine deňdir. Suratda berlen MNPQ trapesiýanyň meýdany ony düzýän F1, F2, F3 figuralaryň meýdanlarynyň jemine deňdir.

1 we 2 häsiýetlere meýdanlaryň esasy häsiýetleri diýilýär. Kesimiň uzynlygynyň hem şuňa meňzeş häsiýetlere eýedigini biz bilýäris.

5. Täze temany berkitmek:

247. 4ABBC. 2AB2BC2AB24AB

=10AB80 sm, AB8 sm. BC4832 sm.

S832256 sm².

Jogaby: 256 sm².

248. (Okuw kitabyndaky 105-nji surat)

PTTMMKPK. P4PT24 sm, PT6 sm.

S_MOKPT  0,75S_PTMK 0,756²  27 sm².

Jogaby: 27 sm².

6. Öý işini tabşyrmak:

1. Meýdanlaryň häsiýetlerini aýdyp beriň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Kwadratyň meýdany
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Kwadratyň meýdany hakynda düşünjeleri öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Köpburçlugyň meýdany hakynda düşünje

3. Geçilen temany jemlemek:

1. Meýdanlaryň häsiýetlerini aýdyp beriň.

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1 Kwadrat barada düşünje bermek.

2. Kwadratyň meýdany barada düşünje bermek

3. Meýdanlaryň häsiýetleri hakynda düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1 Kwadrat barada düşünjeleri bilmeli

2. Kwadratyň meýdany barada bilmeli

3. Meýdanlaryň häsiýetleri hakynda düşünjeleri bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1 Kwadrat barada düşünjeleri bilmegi başarmaly

2. Kwadratyň meýdany barada bilmegi başarmaly

3. Meýdanlaryň häsiýetleri hakynda bilmegi başarmaly

Kwadratyň meýdany. Kwadratyň meýdany onuň tarapynyň kwadratyna deňdir. Eger kwadratyň tarapy kesimleri ölçemegiň saýlanylyp alnan birliginde a san bilen aňladylýan bolsa, onda onuň meýdany a² san bilen aňladylýar. Suratda tarapy 2,1 sm bolan kwadrat şekillendirilendir. Ol dört kwadrat santimetrden we kyrk bir kwadrat millimetrden durýar. Şeýlelik bilen, bu kwadratyň meýdany 4,41 sm²-a deňdir. Bu bolsa kwadratyň tarapynyň kwadratyna deňdir, 4,41 = (2,1)².

Şeýlelik bilen, tarapy a deň bolan kwadratyň meýdany S = a² formula boýunça hasaplanylýar.

1. Deň köpburçluklaryň deň meýdanlary bardyr.

2. Eger köpburçluk käbir köpburçluklardan düzülen bolsa, onda onuň meýdany bu köpburçluklaryň meýdanlarynyň jemine deňdir.

5. Täze temany berkitmek:

249. OP0,5AB bolýandygyny göz öňünde

tutup, AB2OP236 sm ala­rys.

SADAB10660 sm².

Jogaby: 60 sm².

250. ,

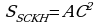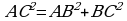
ýa–da ,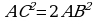

onda

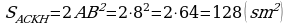
Jogaby: 128 sm².

251. (Okuw kitabyndaky 107-nji surat).

S_OCD 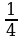 S_ABCD; S_CPD 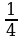 S_DCMK;

S_ABCD  S_DCMK  6²  36 sm².

S_OCPD 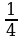 (3636)  18 sm².

Jogaby: 18 sm².

6. Öý işini tabşyrmak:

1. Meýdanlaryň häsiýetlerini aýdyp beriň.

2. Kwadratyň meýdanynyň formulasyny ýazyň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Gönükme çözmek.
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Kwadratyň meýdany hakynda düşünjeleri öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Kwadratyň meýdany

3. Geçilen temany jemlemek:

1. Meýdanlaryň häsiýetlerini aýdyp beriň.

4. Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1 Kwadrat barada düşünje bermek.

2. Kwadratyň meýdany barada düşünje bermek

3 . Meýdanlaryň häsiýetleri hakynda düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1 Kwadrat barada düşünjeleri bilmeli

2. Kwadratyň meýdany barada bilmeli

3. Meýdanlaryň häsiýetleri hakynda düşünjeleri bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1 Kwadrat barada düşünjeleri bilmegi başarmaly

2. Kwadratyň meýdany barada bilmegi başarmaly

3. Meýdanlaryň häsiýetleri hakynda bilmegi başarmaly

Kwadratyň meýdany. Kwadratyň meýdany onuň tarapynyň kwadratyna deňdir. Eger kwadratyň tarapy kesimleri ölçemegiň saýlanylyp alnan birliginde a san bilen aňladylýan bolsa, onda onuň meýdany a² san bilen aňladylýar. Suratda tarapy 2,1 sm bolan kwadrat şekillendirilendir. Ol dört kwadrat santimetrden we kyrk bir kwadrat millimetrden durýar. Şeýlelik bilen, bu kwadratyň meýdany 4,41 sm²-a deňdir. Bu bolsa kwadratyň tarapynyň kwadratyna deňdir, 4,41 = (2,1)².

Şeýlelik bilen, tarapy a deň bolan kwadratyň meýdany S = a² formula boýunça hasaplanylýar.

1. Deň köpburçluklaryň deň meýdanlary bardyr.

2. Eger köpburçluk käbir köpburçluklardan düzülen bolsa, onda onuň meýdany bu köpburçluklaryň meýdanlarynyň jemine deňdir.

5. Täze temany berkitmek:

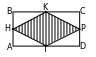252. Iki kateti deň bolan gönüburçly üçburçluklar bolany üçin

HBK=KCP=PDT=TAH. Onda

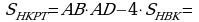
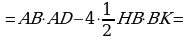
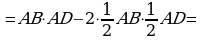
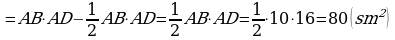
Jogaby: 80 sm².

253. (Okuw kitabyndaky 109-njy surat)

S_ABCD  612  72 sm². BHK we PDT gönüburçly üçburçluklary P no­kat K nokat bilen, T nokat H nokat bilen gabat geler ýaly edip goýsak, ta­rap­lary 3 sm we 6 sm bolan gönüburçlugy alarys. 72 sm²-dan bu gö­nü­burç­lugyň meýdanyny aýryp, gözlenilýän meýdany taparys:

S_AHKCPT  72–18  54 sm².

Jogaby: 54 sm².

6. Öý işini tabşyrmak:

1. Meýdanlaryň häsiýetlerini aýdyp beriň.

2. Kwadratyň meýdanynyň formulasyny ýazyň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Gönüburçlugyň meýdany
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Gönüburçlugyň meýdany hakynda düşünjeleri öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Kwadratyň meýdany

3. Geçilen temany jemlemek:

1. Meýdanlaryň häsiýetlerini aýdyp beriň.

2. Kwadratyň meýdanynyň formulasyny ýazyň.

4. Täze temany düşündirmek:

T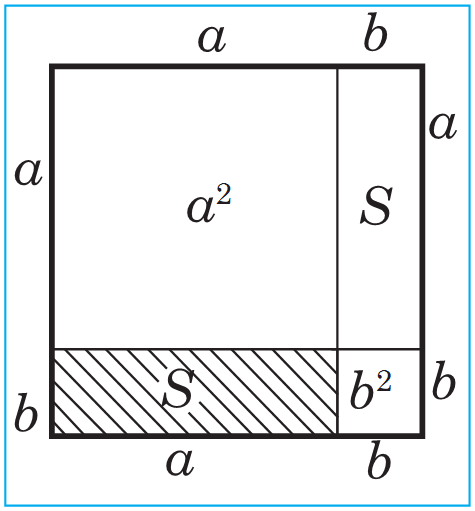 emany düşündirmegiň meýilnamasy:

1 Gönüburçlugyň barada düşünje bermek.

2. Gönüburçlugyň meýdany barada düşünje bermek

3. Meýdanlaryň häsiýetleri hakynda düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1 Gönüburçluk barada düşünjeleri bilmeli

2. Gönüburçlugyň meýdany barada bilmeli

3. Meýdanlaryň häsiýetleri hakynda düşünjeleri bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1 Gönüburçluk barada düşünjeleri bilmegi başarmaly

2. Gönüburçlugyň meýdany barada bilmegi başarmaly

3. Meýdanlaryň häsiýetleri hakynda bilmegi başarmaly

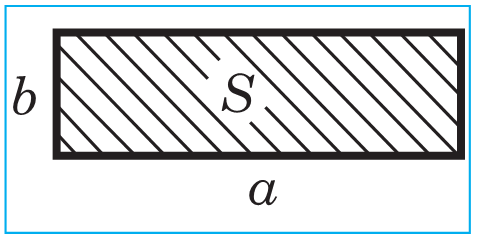Gönüburçlugyň meýdany onuň çatyk taraplarynyň köpeltmek hasylyna deňdir.

Subudy. Taraplary a, b we meýdany S bolan gönüburçluga (sur.) seredeliň.

Bu gönüburçlugy uratda görkezilişi ýaly, tarapy a + b bolan kwadrata çenli dolduralyň. Ol kwadratyň meýdany (a + b)² deňdir.

Bu kwadrat meýdany S bolan berlen gönüburçlukdan, oňa deň bolan S meýdanly ýene bir gönüburçlukdan hem-de meýdanlary a² we b² bolan iki kwadratdan düzülendir. 2-nji häsiýeti ulanyp alarys:

(a + b)² = S + S + a² + b² ýa-da

a² + 2ab + b² = 2S + a² + b².

Bu ýerden 2S=2ab; S=ab alarys.

Teorema subut edildi.

5. Täze temany berkitmek:

254 Subudy. 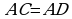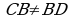(CB)

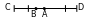S=CBBD bolsa,

S=AD²–AB² subut etmeli

CB=CA–AB=AD–AB

BD=AB+AD, onda

S=CBBD=(AD–AB)(AD–AB)=AD²–AB² S.E.Ş.

255. Perimetri 20sm bolan gönüburçlugyň taraplary a we b bolsun, onda 2(a+b)=20 ýa–da a+b=10.

Perimetri 20sm deň kwadratyň tarapy x bolsun,

onda 4x=20 ýa–da x=5.

Diýmek kwadratyň meýdany S=25 sm².

Indi gönüburçlugyň meýdanyny tapalyň. Onuň taraplary a we 10–a deň, meýdany

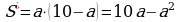
deňdir. Indi olaryň meýdanlarynyň taraplaryna seredeliň

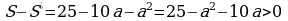
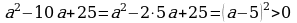
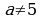bolany üçin.

Bu ýerden kwadratyň meýdanynyň uludygy gelip çykýar.

6. Öý işini tabşyrmak:

1. Meýdanlaryň häsiýetlerini aýdyp beriň.

2. Kwadratyň meýdanynyň formulasyny ýazyň.

3. Gönüburçlugyň meýdanynyň formulasyny getirip çykaryň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________

Mekdebi№: 4 Dersiň ady: Geometriýa

Synpy:	VIII A	VIII B
Senesi:

Sapagyň temasy:	Gönükme çözmek.
Sapagyň maksatlary:
1)Bilim berijilik maksady:	Gönüburçlugyň meýdany hakynda düşünjeleri öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek.
2) Terbiýeçilik maksady:	Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek.
Sapagyň görnüşi:	Täze maglumatlary öwretmek sapagy.
Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar:	Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç.

Sapagyň gidişi:

1. Sapagyň guramaçylyk döwri:

1. Salamlaşmak. Gatnaşygy hasaba almak.

2. Okuwçylaryň ünsüni sapaga gönükdirmek.

3. Syýasy wakalar bilen tanyşdyrmak.

4. Gahryman Arkadagymyzyň «Paýhas çesmesi» «Paýhas çesmesi» kitabyndan sorag-jogap alyşmak.

2. Öý işiniň ýerine ýetirilişini barlamak:

Gönüburçlugyň meýdany

3. Geçilen temany jemlemek:

1. Meýdanlaryň häsiýetlerini aýdyp beriň.

2. Kwadratyň meýdanynyň formulasyny ýazyň.

3. Gönüburçlugyň meýdanynyň formulasyny getirip çykaryň.

4 . Täze temany düşündirmek:

Temany düşündirmegiň meýilnamasy:

1 Gönüburçlugyň barada düşünje bermek.

2. Gönüburçlugyň meýdany barada düşünje bermek

3. Meýdanlaryň häsiýetleri hakynda düşünje bermek

Temany öwrenmek bilen okuwçylar bilmeli:

1 Gönüburçluk barada düşünjeleri bilmeli

2. Gönüburçlugyň meýdany barada bilmeli

3. Meýdanlaryň häsiýetleri hakynda düşünjeleri bilmeli

Temany öwrenmek bilen okuwçylar başarmaly:

1 Gönüburçluk barada düşünjeleri bilmegi başarmaly

2 . Gönüburçlugyň meýdany barada bilmegi başarmaly

3. Meýdanlaryň häsiýetleri hakynda bilmegi başarmaly

Gönüburçlugyň meýdany onuň çatyk taraplarynyň köpeltmek hasylyna deňdir.

Subudy. Taraplary a, b we meýdany S bolan gönüburçluga (sur.) seredeliň.

Bu gönüburçlugy uratda görkezilişi ýaly, tarapy a + b bolan kwadrata çenli dolduralyň. Ol kwadratyň meýdany (a + b)² deňdir.

Bu kwadrat meýdany S bolan berlen gönüburçlukdan, oňa deň bolan S meýdanly ýene bir gönüburçlukdan hem-de meýdanlary a² we b² bolan iki kwadratdan düzülendir. 2-nji häsiýeti ulanyp alarys:

(a + b)² = S + S + a² + b² ýa-da

a² + 2ab + b² = 2S + a² + b².

Bu ýerden 2S=2ab; S=ab alarys.

Teorema subut edildi.

5. Täze temany berkitmek:

256. Diwaryň meýdany

3 m  2,7 m  300 sm  270 sm  81000 sm².

Bir pli­tanyň meýdany 15²225 sm². Onda 81000:225360.

Jogaby: 360 plita gerek.

257. a) Gönüburçlugyň taraplary a we b bolsun, onda onuň meýdany S=ab deňdir.

Diňe bir jübüt garşylykly taraplaryny iki esse ulaltsak onuň meýdany S₁=2ab bolar.

Ilki başdaky meýdandan 2 esse ulalar, S₁=2S.

b) Her bir taraplaryny 2 esse ulaltsak onuň meýdany

S₂=2a2b=4ab deňdir.

Ilki başky meýdandan 4 esse ulalar, ýagny S₂=4S₁ deňlik alnar.

ç) Bu ýagdaýda gönüburçlugyň meýdany

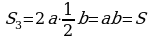bolar, meýdany üýtgemez.

6. Öý işini tabşyrmak:

1. Meýdanlaryň häsiýetlerini aýdyp beriň.

2. Kwadratyň meýdanynyň formulasyny ýazyň.

3. Gönüburçlugyň meýdanynyň formulasyny getirip çykaryň.

7. Sapagy jemlemek we okuwçylaryň bilimlerini bahalandyrmak:

Sapaga işjeň gatnaşan okuwçylary bahalandyrmak.

Ýazan mugallym: M.Işankulyýew

Bellik:________________________________________________________________

Barlan: Müdiriň okuw işleri baradaky orunbasary _____________________________