«Приложения определенного интеграла»
1. Задача о вычислении пути
Пример 1. Скорость прямолинейного движения тела выражается формулой = 2t+3t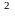 (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.
(м/с). Найти путь, пройденный телом за 5 секунд от начала движения.
S=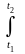 (t)dt, (1)
(t)dt, (1)
Формула(1)
Решение.
t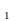 =0с; t
=0с; t  = 5с.
= 5с.
По формуле (1) найдем путь, пройденный телом за 5 сек.
S= 2t+3t
2t+3t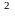 )dt = (t
)dt = (t )
)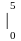 =150(м).
=150(м).
Ответ. S=150 м.
Пример 2. Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью v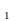 =(6t
=(6t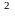 +2t)м/с, второе – со скоростью v
+2t)м/с, второе – со скоростью v =(4t+5)м/с. На каком расстоянии друг от друга они окажутся через 5 с?
=(4t+5)м/с. На каком расстоянии друг от друга они окажутся через 5 с?
Решение. Искомая величина есть разность расстояний, пройденных телами за 5 с.
S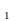 =
= 6 t
6 t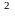 +2t)dt = (2t
+2t)dt = (2t )
)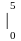 =275(м)
=275(м)
S =
= 4 t+2)dt = (2t
4 t+2)dt = (2t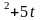 )
)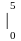 =75(м)
=75(м)
Таким образом, S= S - S
- S =275-75=200(м).
=275-75=200(м).
2.Задача о вычислении работы переменной силы.
Работа A этой силы F вычисляется по формуле:
А=F*s, (2)
Где S – перемещение, м.
Если F – сила упругости, то по закону Гука
F=kx, (2*)
где x- величина растяжения или сжатия,
k – коэффициент пропорциональности.
Работа переменной силы вычисляется по формуле (4)
A=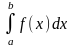 (3)
(3)
Пример. Сила упругости F пружины, растянутой на 1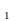 =0,05м, равна 3H. Какую работу надо произвести, чтобы растянуть пружину на 1
=0,05м, равна 3H. Какую работу надо произвести, чтобы растянуть пружину на 1 = 0,1м?
= 0,1м?
Решение
Определим коэффициент пропорциональности k.
Подставим формулу (2*) F=3 H, x = 0,05 м:
3=k*0,0,5, т.е. k=60, следовательно, F=60x=f(x).
Подставив F=60x в формулу (3), найдем значение работы переменной силы, полагая, что а=0; b=0,1:
A= =0,3Дж
Ответ. А = 0,3Дж.
Задача о силе давления жидкости.
Согласно закону Паскаля величина P давления жидкости на горизонтальную площадку вычисляется по формуле
P=gphS, (4)
Где g – ускорение свободного падения в м/с ;
;
p – плотность жидкости в кг/м ;
;
h– глубина погружения площадки в м;
S – площадь площадки в м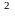 ;
;
Сила давления жидкости на вертикальную пластину вычисляется по формуле (5)
P=g . (5)
Пример.
Аквариум имеет форму прямоугольного параллелепипеда. Найдем силу давления воды (плотность воды 1000 кг/м ), наполняющей аквариум, на одну из его вертикальных стенок, размеры которой 0,4мx0,7м.
), наполняющей аквариум, на одну из его вертикальных стенок, размеры которой 0,4мx0,7м.
Решение
Стенка имеет форму прямоугольника, поэтому f(x)=0.7x, где x[0;0,4], поэтому пределы интегрирования а=0 и b=0,4.
Для нахождения силы давления воды на стену воспользуемся формулой (5).
P=g  =56g549H
=56g549H
g=9,8 м/с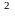 ускорение свободного падения.
ускорение свободного падения.
Самостоятельно решите задачи:
1. Скорость прямолинейного движения тела выражается формулой =9t2-2t-8 (м/с). Найти путь, пройденный телом за 3 секунды от начала движения.
2. Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью v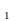 =(2t
=(2t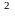 +4t)м/с м/с, второе – со скоростью v
+4t)м/с м/с, второе – со скоростью v =(3t+2)м/м/с. На каком расстоянии друг от друга они окажутся через 10 с?
=(3t+2)м/м/с. На каком расстоянии друг от друга они окажутся через 10 с?
3. Сила упругости F пружины, растянутой на 1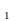 =0,02м, равна 2H. Какую работу надо произвести, чтобы растянуть пружину на 1
=0,02м, равна 2H. Какую работу надо произвести, чтобы растянуть пружину на 1 = 0,05м?
= 0,05м?
4. Вычислить работу, совершенную при сжатии пружины на 0,06 м, если для ее сжатия на 0,01 нужна сила 10 Н.
Таблица 1
| № п/п | Физическая величина | Формула | Единицы измерения |
| 1 | Путь, пройденный точкой с переменной скоростью (t) за отрезок времени [t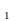 ,t ,t  ] ] | S=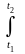 (t)dt (t)dt | t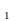 ,t ,t  - с; - с; (t) – м/с; S – м. |
| 2 | Работа переменной силы f(x) на пути от точки a до точки b | A=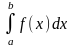
| f(x) – H; a; b – м; A – Дж. |
| 3 | Сила давления жидкости на вертикальную пластину | P=g
| g=9,8 м/с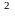 ; ; p – кг/м ; ; a; b – м; р – Н. |







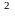 (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.
(м/с). Найти путь, пройденный телом за 5 секунд от начала движения.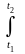 (t)dt, (1)
(t)dt, (1)  =0с; t
=0с; t  = 5с.
= 5с. 2t+3t
2t+3t )
)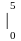 =150(м).
=150(м).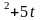 )
)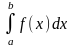 (3)
(3)









