Основные приемы решения тригонометрических уравнений.
1.1 Метод разложения на множители
Метод разложения на множители заключается в следующем: если
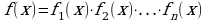 ,
,
то всякое решение уравнения
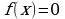 (1.1)
(1.1)
является решением совокупности уравнений:
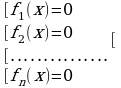 (1.2).
(1.2).
Обратное утверждение, неверно: не всякое решение совокупности уравнений (1.2) является решением уравнения (1.1). Это объясняется тем, что решения отдельных уравнений совокупности (1.2) могут не входить в область определения функции 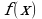 . Поэтому, при решении тригонометрического уравнения необходимо учитывать область допустимых значений исходного уравнения и выбирать только те корни, которые в нее входят.
. Поэтому, при решении тригонометрического уравнения необходимо учитывать область допустимых значений исходного уравнения и выбирать только те корни, которые в нее входят.
При решении тригонометрических уравнений с помощью разложения на множители очень часто необходимо преобразовать сумму или разность тригонометрических функций в произведение.
Пример 1.1. Решите уравнение
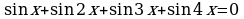 .
.
Решение.
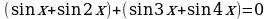
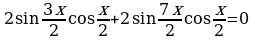
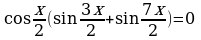
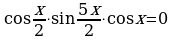
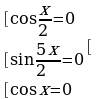
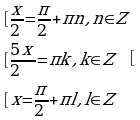
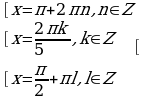
Ответ: 
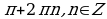 ;
; 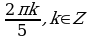 ;
; 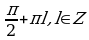 .
.
1.2 Метод замены переменной
Данный метод позволяет с помощью введения новой переменной, свести решение тригонометрического уравнения к решению алгебраического уравнения.
Пример 1.2. Решите уравнение
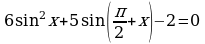
Решение.
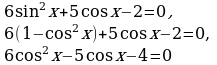
Замена: 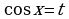 ,
, 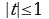
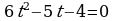
t1 = -1/2, t2=4/3
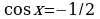
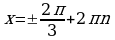 ,
, 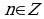 .
.
Ответ: 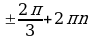 ,
,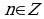
1.3 Уравнения, решаемые с помощью формул понижения степени
Решение многих тригонометрических уравнений, содержащих функции в четных степенях, основано на применении формул понижения степени:
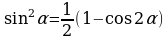
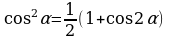
Очень часто эти формулы применяются в виде:
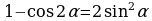
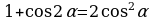
Пример 1.3. Решите уравнение
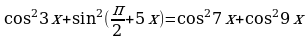 .
.
Решение

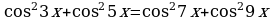
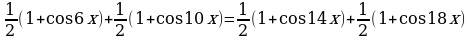
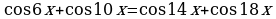
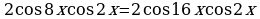
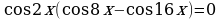
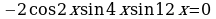
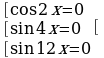 ;
; 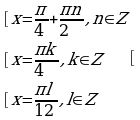 ;
; 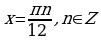
Ответ: 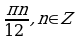 .
.
1.4. Уравнения, однородные относительно синуса и косинуса
Определение. Уравнение вида 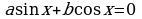 , где
, где 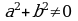 называется однородным тригонометрическим уравнением первой степени.
называется однородным тригонометрическим уравнением первой степени.
Определение. Уравнение вида 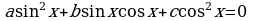 , где
, где 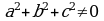 называется однородным тригонометрическим уравнением второй степени.
называется однородным тригонометрическим уравнением второй степени.
Однородные уравнения первой степени.
Чтобы решить однородное уравнение вида
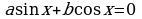 , где
, где 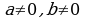
нужно обе его части разделить на 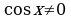 или
или 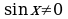 , получив простейшее тригонометрическое уравнение
, получив простейшее тригонометрическое уравнение
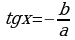 или
или 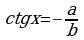 .
.
В случае, когда один из коэффициентов, а либо b, равен нулю, однородное уравнение первой степени сводится к простейшему тригонометрическому уравнению
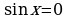 или
или 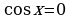 .
.
Однородные уравнения второй степени.
I. Однородное уравнение второй степени
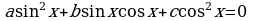 , где
, где 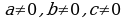 ,
,
делится на 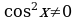 либо на
либо на 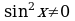 и приводится к квадратному уравнению
и приводится к квадратному уравнению
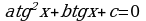 или
или 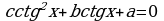 ,
,
которые решаются методом замены переменной, полагая 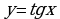 или
или 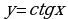 .
.
II. Если 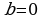 ,
, 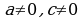 , уравнение имеет вид:
, уравнение имеет вид:
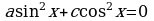 ,
,
уравнение делится на 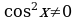 либо на
либо на 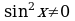 и приводится к виду:
и приводится к виду:
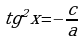 или
или 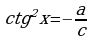 .
.
III. Если 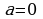 ,
, 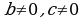 , уравнение имеет вид:
, уравнение имеет вид:
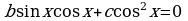 .
.
Решается методом разложения на множители, и сводится к решению простейшего тригонометрического уравнения и однородного уравнения первой степени:
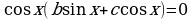
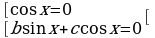
IV. Если 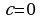 ,
, 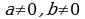 , уравнение имеет вид:
, уравнение имеет вид:
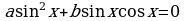 .
.
Решается аналогично случаю III:
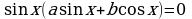
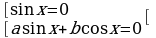
Пример 1.4. Решите уравнение
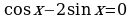 .
.
Решение
Разделим на 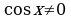 обе части уравнения (т.к.
обе части уравнения (т.к. 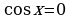 не является решением уравнения, то без потери корней можем считать
не является решением уравнения, то без потери корней можем считать 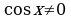 ):
):
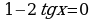 ;
; 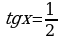 ;
; 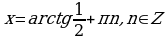 .
.
Ответ: 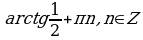 .
.
Пример 1.5. Решите уравнение
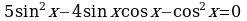
Решение.
Разделив обе части уравнения на 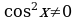 , получим уравнение:
, получим уравнение:
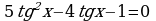 .
.
Замена: 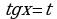
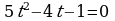
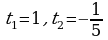
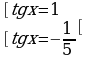
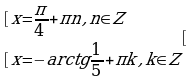
Ответ: 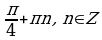 ,
, 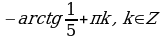 .
.







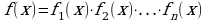 ,
,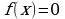 (1.1)
(1.1)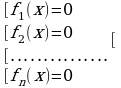 (1.2).
(1.2).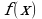 . Поэтому, при решении тригонометрического уравнения необходимо учитывать область допустимых значений исходного уравнения и выбирать только те корни, которые в нее входят.
. Поэтому, при решении тригонометрического уравнения необходимо учитывать область допустимых значений исходного уравнения и выбирать только те корни, которые в нее входят.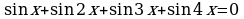 .
.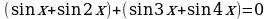
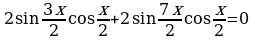
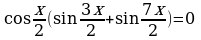
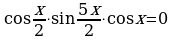
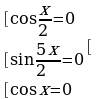
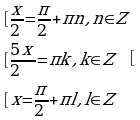
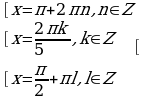

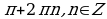 ;
; 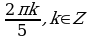 ;
; 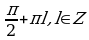 .
.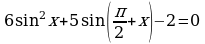
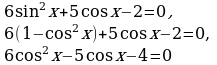
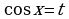 ,
, 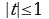
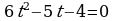
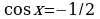
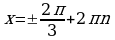 ,
, 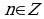 .
.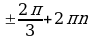 ,
,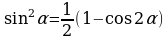
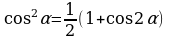
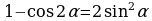
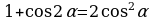
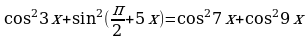 .
.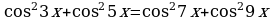
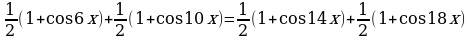
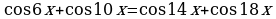
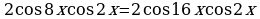
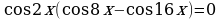
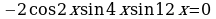
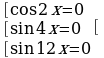 ;
; 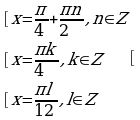 ;
; 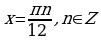
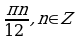 .
.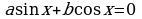 , где
, где 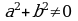 называется однородным тригонометрическим уравнением первой степени.
называется однородным тригонометрическим уравнением первой степени. 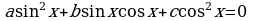 , где
, где 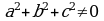 называется однородным тригонометрическим уравнением второй степени.
называется однородным тригонометрическим уравнением второй степени.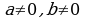
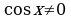 или
или 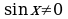 , получив простейшее тригонометрическое уравнение
, получив простейшее тригонометрическое уравнение 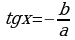 или
или 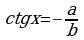 .
.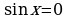 или
или 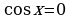 .
.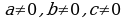 ,
,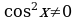 либо на
либо на 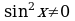 и приводится к квадратному уравнению
и приводится к квадратному уравнению 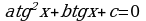 или
или 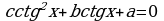 ,
,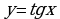 или
или 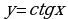 .
.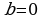 ,
, 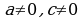 , уравнение имеет вид:
, уравнение имеет вид: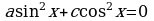 ,
,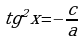 или
или 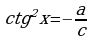 .
.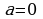 ,
, 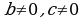 , уравнение имеет вид:
, уравнение имеет вид: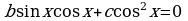 .
.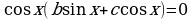
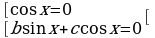
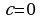 ,
, 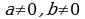 , уравнение имеет вид:
, уравнение имеет вид: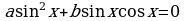 .
.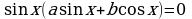
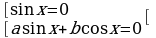
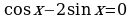 .
.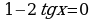 ;
; 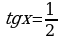 ;
; 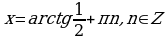 .
.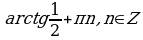 .
.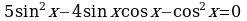
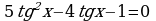 .
.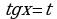
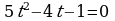
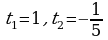
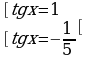
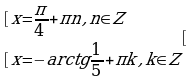
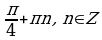 ,
, 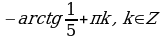 .
.

















