Ачык сабак Ромб

Предмет: Геометрия 7-класс

Сабактын темасы: Ромб.

Сабактын максаты: 1. Билим берүүчүлүк:

Окуучулар ромб жөнүндө түшүнүк алышат.

2. Өнүктүрүүчүлүк:

Окуучулар ромбдун формуласын

билишет,мисалдарды иштейт аныктамасын айтып

беришет.

3. Тарбия берүүчүлүк:

Окуучулар бири-бирин сөзүн уга билип,башкалардын

ой пикирин урматтоо менен кабыл

алууга тарбияланышат.

Сабактын тиби: Жаңы билимди өздөштүрүү.

Сабактын жабдылышы: Слайд,тесттик суроолор,баш катырмалар,видео

ролик ж.б

Сабактын жүрүшү:

1. Саламдашуу.дептерлерди текшерүү,катышууну аныктоо,классты

1. топко бөлүп сабакка даярдоо.

1. Уй тапшырмасын текшеруу.

3.Жаңы теманы түшүндүрүү

4.Бышыктоо: кахут программасы менен тест аркылуу.

5.Үйгө тапшырма берүү

6.Баалоо

Ромб.

Ромб (грекче rhomboc) – жактары барабар болгон параллелограмм. Диагоналдары өз ара перпендикуляр жана алардын кесилишинде тең экиге бөлүнүшөт. Тик бурчтуу Ромб квадрат деп аталат. Ромбдун аянты: S = d^dj2 же S = a²sina, мында a – жагы, d_t ,d₂ - диагоналдары, a – бурчтарынын бири.

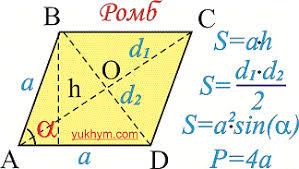
АВСD ромб . Ал пареллограммдын бир түрү болгондуктан пареллограммдын бардык касиеттери жана ал жөнүндөгү теоремалар ромб үчүн да туура болот.

Мында АВ = ВС= СD = DA болору түшүнүктүү .

Ромбдун диагоналдары өз ара перпендикулярдуу жана алар бурчтарын тең экиге бөлөт.

Далилдөө: АВСD АС ВD –диагоналдар АС ВD 1= 2 болоорун далилдейбиз.

АО= ОС АВD –тен капталдуу анда DО мединасы анын бийиктиги да биссектрисасы да болот.

41-теорема: Эгерде пареллограммдын диагоналдары перпендикулярдуу болушса, анда ал ромб болот.

Ромдун формулалы

А