Адаптированная рабочая программа по алгебре

Муниципальное бюджетное общеобразовательное учреждение основная общеобразовательная школа с. Салихово МР Ишимбайский Республики Башкортостан

Адаптированная рабочая программа

по алгебре

на ступень 7-9 классы

Срок реализации 2019-2024гг.

Составила учитель первой категории Габбасова Н.А.

с.Салихово - 2019

Пояснительная записка

Индивидуальная образовательная траектория составлена на основе Программы «Алгебра 7 – 9 классы. Москва «Мнемозина», 2014 г. Авторы и составители: И.И.Зубарева, А.Г.Мордкович.

Содержание индивидуальной образовательной траектории адаптировано в соответствии с образовательными потребностями и индивидуальными возможностями обучающегося с ОВЗ с учетом рекомендаций обучения детей с ОВЗ.

Важными коррекционно-развивающими задачами курса алгебры являются:

• развитие у обучающихся основных мыслительных операций (анализ, синтез, сравнение, обобщение);

• нормализация взаимосвязи деятельности с речью;

• формирование приемов умственной работы (анализ исходных данных, планирование деятельности, осуществление поэтапного и итогового самоконтроля);

• развитие речи, умения использовать при пересказе соответствующую терминологию;

• развитие УУД.

Усвоение учебного материала вызывает затруднения у учащихся с ОВЗ в связи их особенностями: быстрая утомляемость, недостаточность абстрактного мышления, недоразвитие пространственных представлений, низкие общеучебные умения и навыки. Учет особенностей учащихся с ОВЗ требует, чтобы при изучении нового материала обязательно происходило многократное его повторение, подробное рассмотрение тем и вопросов, раскрывающих связь предмета с жизнью, актуализация первичного жизненного опыта обучающихся.

Для эффективного усвоения обучающимися с ОВЗ учебного материала в системе работы учителя на уроке делают акцент при изучении тем и вопросов, на практическую направленность, частое повторение слабо усвоенных тем и решения задач; увеличено время на проведение лабораторных работ под руководством учителя.

Содержание интегрированного обучения детей в общеобразовательном учреждении определена разработанными индивидуальными траекториями образования и развития, по предмету разработанная и реализуемая общеобразовательным учреждением самостоятельно на основе государственных образовательных стандартов и примерных образовательных учебных программ.

Индивидуальная траектория образования и развития выступает правовой основой инклюзии учащихся с ОВЗ и успешность усвоения рассматривается по итогам каждой четверти на школьной ПМПК.

При желании родителей (законных представителей) могут отказаться от интегрированного обучения и продолжить обучение по ранее осваиваемой образовательной программе в специальной (коррекционной) школе.

Специфика образовательного процесса в системе интегрированного обучения детей с ограниченными возможностями здоровья состоит в организации дополнительных, индивидуальных и групповых коррекционно-развивающих занятий, кроме занятий в классе совместно со здоровыми сверстниками.

Общеобразовательное учреждение, учителя предметники самостоятельно выбирают формы, средства и методы интегрированного обучения и воспитания в соответствии с Законом Российской Федерации «Об образовании» и уставом образовательного учреждения. При определении реабилитационной составляющей интегрированного обучения учитель ориентируется на рекомендации ПМПК.

Интегрированное образование имеет развивающей характер (раскрытие потенциала, возможностей ребенка), когда учитель и специалисты ППиМСс ведут сопровождение учебного процесса, ориентируются на средне возрастные нормы развития и создают условия в которых ребенок сможет подняться на оптимальный для него уровень развития.

Индивидуальная траектория образования и развития для детей с ОВЗ проектируется с учетом следующих этапов:

- мотивационный: совместное обследование на школьном ПМПК условий сотрудничества учителей и специалистов службы ППиМСс;

- концептуальный: формирование общих целей, задач, распределение обязанностей по сопровождению детей с ОВЗ;

- проектный: разработка индивидуальной траектории образования и развития для детей с ОВЗ на основе диагностических данных;

В Индивидуальной траектории образования и развития для детей с ОВЗ предусматривается планирование результатов работы, использование индивидуальных методов обучения и воспитания, ведение мониторинга успешного освоения основной образовательной программы среднего (полного) образования.

- практическая: реализация программы: тенденция педагогической деятельности, анализ, рефлексия, разрешение затруднений при переходе на следующую ступень в образовании.

Режим интегрированного обучения осуществляется с учетом режима общеобразовательного учреждения.

Принципы формирования индивидуальной образовательной траектории:

• Служит средством приспособления к широкому кругу возможностей ученика;

• Является способом выражения, принятия и уважения индивидуальных особенностей обучения;

• Применима ко всем составным частям программы и к привычной манере поведения в классе;

• Является обязательной для всех работников, вовлеченных в процесс обучения.

• Составлена с целью повышения успешности ученика.

2. Особенности инклюзивного образования на уроке

Инклюзивное (включающее) образование в школе дает возможность учащимся с ОВЗ в полном объеме участвовать в жизни коллектива школьной жизни и вхождению их в образовательный процесс и внешкольные мероприятия проводимые по предмету, а так же на формирование толерантного отношения к обучающимся с ОВЗ.

Такой подход на уроках обладает ресурсами, направленными на стимулирование равноправия обучающихся и их участия во всех этапах образовательного процесса, а так же на развитие способностей, необходимых для общения. Для обучающихся с ОВЗ, позиция учителя базируется на следующих аспектах: ценностно-смысловом, программно-методическом, психологическом, педагогическом, социальном,

• Принцип равных возможностей;

• Каждый человек способен чувствовать и думать;

• Для всех обучающихся достижение скорее в том, что они могут делать, чем в том, что не могут;

• Внимание на возможности и сильные стороны ребенка;

• Раскрытие каждого ученика с помощью образовательной программы предмета;

• Фокусирование при обучении не только на действия, но и на цели;

• Организация обучения, с учетом образовательных потребностей обучающихся;

• Индивидуальная помощь не отделяет и не изолирует обучающихся;

• Способствовать позитивной адаптации к жизни;

• Акцент на успешность обучающихся;

• Внимание при обучении детей тому, что поможет им занять активную жизненную позицию;

• Побуждать всех детей в классе помогать друг другу;

• Норма, когда даются разные задания и ожидаются от обучающихся разные результаты;

• Повышение уровня мотивации и улучшение результатов детей с особыми образовательными потребностями.

Результаты инклюзии на уроке:

• У учеников есть возможность активного и постоянного участия во всех этапах урока.

• Адаптация урока и не содействует выработке негативных стереотипов.

• Методы урока направлены на включение ученика в деятельность и возможности для обобщения и передачи навыков.

3. Учет психологических особенностей детей с ОВЗ в учебной деятельности

Задержка психического развития (ЗПР) – VII вид обучения

У детей с ЗПР имеется ряд специфических особенностей в их познавательной, эмоционально-волевой деятельности, поведении и личности в целом, характерные для большинства детей этой категории:

повышенная истощаемость и в результате нее низкая работоспособность; незрелость эмоций, воли, поведения; ограниченный запас общих сведений и представлений; бедный словарный запас, несформированность навыков интеллектуальной деятельности; игровая деятельность сформирована также не полностью; восприятие замедленное; в мышлении трудности словесно-логических операций; страдают все виды памяти; отсутствуют умения использовать вспомогательные средства для запоминания. Им необходим более длительный период для приема и переработки информации. Многие практические и интеллектуальные задачи они решают на уровне своего возраста, способны воспользоваться оказанной помощью, умеют осмыслить сюжет картинки, рассказа, разобраться в условии простой задачи и выполнить множество других заданий. У этих обучающихся отмечается недостаточная познавательная активность, которая в сочетании с быстрой утомляемостью и истощаемостью может серьезно тормозить их обучение и развитие. Быстро наступающее утомление приводит к потере работоспособности, вследствие чего у обучающихся возникают затруднения в усвоении учебного материала: они не удерживают в памяти условия задачи, продиктованное предложение, забывают слова; допускают нелепые ошибки в письменных работах; нередко вместо решения задачи просто механически манипулируют цифрами; оказываются неспособными оценить результаты своих действий; их представления об окружающем мире недостаточно широки, не могут сосредоточиться на задании, не умеют подчинять свои действия правилам, содержащим несколько условий.

В периоды нормальной работоспособности у детей с ЗПР обнаруживается целый ряд положительных сторон их деятельности, характеризующих сохранность многих личностных и интеллектуальных качеств. Эти сильные стороны проявляются чаще всего при выполнении детьми доступных и интересных заданий, не требующих длительного умственного напряжения и протекающих в спокойной доброжелательной обстановке.

В таком состоянии при индивидуальной работе с ними дети оказываются способными самостоятельно или с незначительной помощью решать интеллектуальные задачи почти на уровне нормально развивающихся сверстников (производить группировку предметов, устанавливать причинно-следственные связи в рассказах со скрытым смыслом, понимать переносный смысл пословиц).

Во внеклассной жизни дети обычно активны, интересы их, как и у нормально развивающихся детей, разнообразны. Некоторые из них предпочитают тихие, спокойные занятия – лепку, рисование, конструирование, с увлечением работают со строительным материалом и разрезными картинками. Но таких детей меньшинство. Большинство предпочитают подвижные игры, любят побегать, порезвиться. К сожалению, и у «тихих», и у «шумных» детей фантазии и выдумки в самостоятельных играх, как правило, бывает мало.

Все дети с ЗПР любят разного рода экскурсии, посещение театров, кинотеатров и музеев, иногда это их так захватывает, что они несколько дней находятся под впечатлением увиденного. Любят занятия физкультурой и спортивные игры, и, хотя у них обнаруживается явная двигательная неловкость, недостаточная координированность движений, неумение подчиняться заданному (музыкальному или словесному) ритму, со временем, в процессе обучения, школьники достигают значительных успехов.

Дети с ЗПР дорожат доверием взрослых, но это не избавляет их от срывов, часто происходящих помимо их воли и сознания, без достаточных на то оснований. Потом они с трудом приходят в себя и еще, долго чувствуют неловкость, угнетенность.

Учет особенностей развития детей с ЗПР чрезвычайно важно для понимания общего подхода к работе с ними на уроке и внеклассной деятельности.

Математическое образование в основной школе складывается из следующих содержательных компонентов (учебных блоков): арифметика; алгебра; геометрия; элементы комбинаторики, тео­рии вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обу­чения математике в нашей стране, учитывают современные тенденции отечественной и зарубеж­ной школы и позволяют реализовать поставленные перед школьным образованием цели на ин­формационно емком и практически значимом материале.

Алгебра нацелена на формирование математического аппарата для решения задач из матема­тики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение мате­матики как языка для построения математических моделей процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, не­обходимого, в частности, для освоения курса информатики, а также овладение навыками дедук­тивных рассуждений. Преобразование символических форм способствует развитию воображе­ния, способностей к математическому творчеству. Другой важной задачей изучения алгебры яв­ляется получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования представлений о роли математики в развитии цивилизации и культуры.

Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязатель­ным компонентом школьного образования, усиливающим его прикладное и практическое значе­ние. Этот материал необходим для формирования функциональной грамотности - умений вос­принимать и анализировать информацию, представленную в различных формах, понимать веро­ятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение слу­чаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.

При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источ­ника социально значимой информации и закладываются основы вероятностного мышления.

I. Цели изучения предмета.

Изучение математики в основной школе направлено на достижение следующих целей:

1) в направлении личностного развития:

• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;

• формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

• воспитание качеств личности, обеспечивающих социальную мобильность, способность

принимать самостоятельные решения;

• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

• развитие интереса к математическому творчеству и математических способностей;

2) в метапредметном направлении:

• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;

3) в предметном направлении:

• овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, для изучения смежных дисциплин, применения в повседневной жизни;

• создание фундамента математического развития, формирования механизмов мышления, характерных для математической деятельности

II. Общая характеристика учебного предмета «Алгебра»

В курсе алгебры можно выделить следующие основные со­держательные линии: арифметика; алгебра; функции; вероят­ность и статистика. Наряду с этим в содержание включены два дополнительных методологических раздела: логика и множества; математика в историческом развитии, что связано с реализаци­ей целей общеинтеллектуального и общекультурного развития учащихся. Содержание каждого из этих разделов разворачива­ется в содержательно-методическую линию, пронизывающую все основные содержательные линии. При этом первая ли­ния — «Логика и множества» — служит цели овладения учащи­ мися некоторыми элементами универсального математического языка, вторая — «Математика в историческом развитии» — спо­собствует созданию общекультурного, гуманитарного фона из­учения курса.

Содержание линии «Арифметика» служит базой для даль­нейшего изучения учащимися математики, способствует раз­витию их логического мышления, формированию умения поль­зоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие по­нятия о числе в основной школе связано с рациональными и иррациональными числами, формированием первичных пред­ставлений о действительном числе.

Содержание линии «Алгебра» способствует формированию у учащихся математического аппарата для решения задач из раз­делов математики, смежных предметов и окружающей реально­сти. Язык алгебры подчёркивает значение математики как язы­ка для построения математических моделей процессов и явле­ний реального мира.

Развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, и овладение навыками дедуктивных рассуждений также являются задачами изучения алгебры. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной шко­ле материал группируется вокруг рациональных выражений.

Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разно­образных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в раз­витии цивилизации и культуры.

Раздел «Вероятность и статистика» — обязательный компо­нент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде все­го, для формирования у учащихся функциональной грамот­ности— умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, про­изводить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотре­ние случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.

При изучении статистики и вероятности обогащаются пред­ставления о современной картине мира и методах его исследо­вания, формируется понимание роли статистики как источни­ка социально значимой информации и закладываются основы вероятностного мышления.

III. Место предмета в федеральном базисном учебном плане.

Базисный учебный (образовательный) план на изучение математики в 7-9 классах отводит 5 учебных часов в неделю в течение каждого года обучения, всего 510 часов, из них 306 часов -на изучение алгебры и 204 часов - на изучение геометрии.

С учетом требований Федерального государственного образовательного стандарта основного общего образования в содержании рабочей программы предполагается реализовать компетентностный, личностно ориентированный и деятельностный подходы, которые определяют задачи обучения: приобретение математических знаний и умений; освоение универсальных учебных действий.

Компетентностный подход определяет следующие особенности предъявления содержания образования: оно представлено в виде трех тематических блоков, обеспечивающих формирова­ние компетенций. В первом блоке представлены дидактические единицы, обеспечивающие со­вершенствование математических навыков. Во втором - дидактические единицы, которые со­держат сведения из истории математики. Это содержание обучения является базой для развития коммуникативной компетенции учащихся. В третьем блоке представлены дидактические едини­цы, отражающие информационную компетенцию и обеспечивающие развитие учебно-познава­тельной и рефлексивной компетенций. Таким образом, рабочая программа обеспечивает взаимо­связанное развитие и совершенствование ключевых, общепредметных и предметных компетен­ций.

Принципы отбора содержания связаны с преемственностью целей образования на различных ступенях и уровнях обучения, логикой внутрипредметных связей, а также с возрастными осо­бенностями развития учащихся.

Личностная ориентация образовательного процесса выявляет приоритет воспитательных и развивающих целей обучения. Способность учащихся понимать причины и логику развития математических процессов открывает возможность для осмысленного восприятия всего разнооб­разия мировоззренческих, социокультурных систем, существующих в современном мире. Систе­ма учебных занятий призвана способствовать развитию личностной самоидентификации, гума­нитарной культуры школьников, их приобщению к естественно-математической культуре, уси­лению мотивации к социальному познанию и творчеству, воспитанию личностно и общественно востребованных качеств, в том числе гражданственности, толерантности.

Деятельностный подход отражает стратегию современной образовательной политики: необ­ходимость воспитания человека и гражданина, интегрированного в современное ему общество, нацеленного на совершенствование этого общества. Система уроков сориентирована не столько на передачу готовых знаний, сколько на формирование активной личности, мотивированной к самообразованию, обладающей достаточными навыками и психологическими установками к самостоятельному поиску, отбору, анализу и использованию информации. Это поможет выпу­скнику адаптироваться в мире, где объем информации растет в геометрической профессии, где социальная и профессиональная успешность напрямую зависят от позитивного отношения к но­вациям, самостоятельности мышления и инициативности, от готовности проявлять творческий подход к делу, искать нестандартные способы решения проблем, конструктивно взаимодейство­вать с людьми.

Основой целеполагания является обновление требований к уровню подготовки выпускников в системе естественно-математического образования, отражающее важнейшую особенность пе­дагогической концепции государственного стандарта - переход от суммы «предметных резуль­татов» (то есть образовательных результатов, достигаемых в рамках отдельных учебных предме­тов) к межпредметным и интегративным результатам. Такие результаты представляют собой обобщенные способы деятельности, которые отражают специфику не отдельных предметов, а ступеней общего образования. В государственном стандарте они зафиксированы как универ­сальные учебные действия, что предполагает повышенное внимание к развитию межпредмет­ных связей курса математики.

Дидактическая модель обучения и педагогические средства отражают модернизацию основ учебного процесса, их переориентацию на достижение конкретных результатов в виде сформи­рованных регулятивных, коммуникативных и познавательных учебных умений. Формирование целостных представлений о математике будет осуществляться в ходе творческой деятельности учащихся на основе личностного осмысления математических фактов и явлений. Особое внима­ние уделяется познавательной активности учащихся, их мотивированности к самостоятельной учебной работе. Это предполагает все более широкое использование нетрадиционных форм уро­ков, в том числе методики деловых и ролевых игр, проблемных дискуссий, межпредметных интегрированных уроков и т. д.

Планируется использование следующих технологий в преподавании предмета:

• технологии полного усвоения;

• технологии обучения на основе решения задач;

• технологии обучения на основе схематических и новых знаковых моделей.

Для естественно-математического образования приоритетным можно считать развитие уме­ний самостоятельно и мотивированно организовывать свою познавательную деятельность, ис­пользовать элементы причинно-следственного и структурно-функционального анализа, опреде­лять сущностные характеристики изучаемого объекта, самостоятельно выбирать критерии для сравнения, сопоставления, оценки и классификации объектов - в программе это является осно­вой для целеполагания.

На ступени основной школы задачи учебных занятий (в схеме - планируемый результат) оп­ределены как закрепление умений разделять процессы на этапы, звенья, выделять характерные причинно-следственные связи, определять структуру объекта познания, значимые функциональ­ные связи и отношения между частями целого, сравнивать, сопоставлять, классифицировать, ранжировать объекты по одному или нескольким предложенным основаниям, критериям. Прин­ципиальное значение в рамках курса приобретает умение различать факты, мнения, доказатель­ства, гипотезы, аксиомы.

При выполнении творческих работ формируется умение определять адекватные способы ре­шения учебной задачи на основе заданных алгоритмов, комбинировать известные алгоритмы де­ятельности в ситуациях, не предполагающих стандартного применения одного из них, мотивиро­ванно отказываться от образца деятельности, искать оригинальные решения.

Учащиеся должны приобрести умения по формированию собственного алгоритма решения познавательных задач, уметь формулировать проблему и цели своей работы, определять адек­ватные способы и методы решения задачи, прогнозировать ожидаемый результат и сопоставлять

его с собственными математическими знаниями. Учащиеся должны научиться представлять ре­зультаты индивидуальной и групповой познавательной деятельности в формах конспекта, рефе­рата, рецензии.

Реализация рабочей программы обеспечивает освоение коммуникативных учебных действий, в том числе способностей передавать содержание текста в сжатом или развернутом виде в соответ­ствии с целью учебного задания, проводить информационно-смысловый анализ текста, составлять план, тезисы, конспект. На уроках учащиеся более уверенно овладеют монологической и диалоги­ческой речью, умением вступать в речевое общение, участвовать в диалоге (понимать точку зрения собеседника, признавать право на иное мнение), научатся приводить примеры, подбирать аргумен­ты, перефразировать мысль, формулировать выводы. Для решения познавательных и коммуника­тивных задач учащимся предлагается использовать различные источники информации, включая энциклопедии, словари, Интернет-ресурсы и другие базы данных, в соответствии с коммуникатив­ной задачей, сферой и ситуацией общения осознанно выбирать выразительные средства языка и знаковые системы.

В процессе обучения должно быть сформировано умение формулировать свои мировоззрен­ческие взгляды как основа духовно-нравственного развития школьника.

Описание ценностных ориентиров содержания учебного предмета

Курс характеризуется повышением теоретического уровня обучения, постепенным усилением роли теоретических обобщений и дедуктивных заключений. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения алгебры к изучению действительности и решению практических задач. Главная задача УМК А.Г. Мордковича заключается не в сухом сообщении математических фактов, а в развитии учащихся посредством продвижения в предмете, т.е. приоритетным является не информационное, а развивающее поле курса.

Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.

Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений). Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.

Требования к результатам освоения основной образовательной программы в соответствии с ФГОС ОО

I. Личностные результаты:

Формирование ответственного отношения к учению, готовности к саморазвитию и самообразованию на основе мотивации к обучению, осознанному построению индивидуальной образовательной траектории с учетом устойчивых познавательных интересов, выбору профильного математического образования.

Формирование целостного мировоззрения, соответствующего современному уровню развития науки.

Формирование коммуникативной компетентности в учебно-исследовательской, творческой и других видах деятельности.

II.Метапредметные результаты:

- Формирование универсальных учебных действий (познавательных, регулятивных, коммуникативных), обеспечивающих овладение ключевыми компетенциями, составляющими основу умения учиться.

- Формирование умения самостоятельно ставить учебные и познавательные задачи, преобразовывать практическую задачу в теоретическую и наоборот.

- Формирование умения планировать пути достижения целей, выделять альтернативные способы достижения цели, выбирать наиболее рациональные методы, осуществлять познавательную рефлексию в отношении действий по решению учебных и познавательных задач.

- Формирование осознанной оценки в учебной деятельности, умения содержательно обосновывать правильность результата и способа действия, адекватно оценивать свои возможности достижения цели самостоятельной деятельности.

- Формирование умения логически рассуждать, делать умозаключения (индуктивное, дедуктивное и по аналогии), аргументированные выводы, умение обобщать, сравнивать, классифицировать.

- Формирование умения создавать, применять и преобразовывать знаково-символические средства, модели, схемы для решения учебных и познавательных задач.

- Овладение основами ознакомительного, изучающего, усваивающего и поискового чтения, рефлексивного чтения, формирование умения структурировать математические тексты, выделять главное, выстраивать логическую последовательность излагаемого материала.

- Формирование компетентности в области использования ИКТ, как инструментальной основы развития универсальных учебных действий.

III.Предметные результаты:

1. Формирование представлений о математике как о части общечеловеческой культуры, форме описания и особого метода познания действительности.

2. Формирование представления об основных изучаемых понятиях как важнейших математических моделях, позволяющих описывать реальные процессы.

3. Развитие умений работать с учебным математическим текстом, грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификацию, логическое обоснование и доказательства математических утверждений, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения.

4. Формирование представлений о системе функциональных понятий, функциональном языке и символике; развитие умения использовать функционально – графические представления для решения различных математических задач, в том числе: решения уравнений и неравенств, нахождения наибольшего и наименьшего значений, для описания и анализа реальных зависимостей и простейших параметрических исследований.

5. Овладение символьным языком алгебры, приемами выполнения тождественных преобразований выражений, решения линейных уравнений и систем линейных уравнений, а также уравнений, решение которых сводится к разложению на множители; развитие умений моделировать реальные ситуации на математическом языке, составлять уравнения по условию задачи, исследовать построенные модели и интерпретировать результат. Развитие умений использовать идею координат на плоскости для решения уравнений, неравенств, систем.

6. Овладение основными способами представления и анализа статистических данных; формирование представлений о статистических закономерностях в реальном мире и способах их изучения, о простейших вероятностных моделях. Развитие умения извлекать информацию, представленную в таблицах, на диаграммах, графиках, описывать и анализировать числовые данные, использовать понимание вероятностных свойств окружающих явлений при принятии решений.

7. Развитие умений применять изученные понятия для решения задач практического содержания и задач смежных дисциплин.

Содержание учебного предмета «Алгебра» 7-9 классы

Арифметика

Рациональные числа. Расширение множества натуральных чисел до множества целых. Множества целых чисел до множества рациональных. Рациональное число как отношение m/n, где m — целое число, п — натуральное. Степень с целым показа­телем.

Действительные числа. Квадратный корень из числа. Ко­рень третьей степени. Запись корней с помощью степени с дробным показателем.

Понятие об иррациональном числе. Иррациональность чис­ла и несоизмеримость стороны и диагонали квадрата. Десятич­ные приближения иррациональных чисел.

Множество действительных чисел; представление действи­тельных чисел бесконечными десятичными дробями. Сравне­ние действительных чисел.

Измерения, приближения, оценки. Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире. Выделение мно­жителя — степени десяти в записи числа. Приближённое зна­чение величины, точность приближения. Прикидка и оценка результатов вычислений.

Алгебра

Алгебраические выражения. Буквенные выражения (вы­ражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных. Подстановка выражений вместо переменных. Преобразование буквенных выражений на основе свойств арифметических действий. Ра­венство буквенных выражений. Тождество.

Степень с натуральным показателем и её свойства. Одно­члены и многочлены. Степень многочлена. Сложение, вычита­ние, умножение многочленов. Формулы сокращённого умно­жения: квадрат суммы и квадрат разности. Формула разности квадратов. Преобразование целого выражения в многочлен. Разложение многочленов на множители. Многочлены с одной переменной. Корень многочлена. Квадратный трёхчлен; разло­жение квадратного трёхчлена на множители.

Алгебраическая дробь. Основное свойство алгебраической дроби. Сложение, вычитание, умножение, деление алгебраиче­ских дробей. Степень с целым показателем и её свойства.

Рациональные выражения и их преобразования. Доказа­тельство тождеств.

Квадратные корни. Свойства арифметических квадратных корней и их применение к преобразованию числовых выраже­ний и вычислениям.

Уравнения. Уравнение с одной переменной. Корень урав­нения. Свойства числовых равенств. Равносильность уравнений.

Линейное уравнение. Квадратное уравнение: формула кор­ней квадратного уравнения. Теорема Виета. Решение уравне­ний, сводящихся к линейным и квадратным. Примеры решения уравнений третьей и четвёртой степеней. Решение дробно-ра­циональных уравнений.

Уравнение с двумя переменными. Линейное уравнение с двумя переменными, примеры решения уравнений в целых числах.

Система уравнений с двумя переменными. Равносильность систем. Системы двух линейных уравнений с двумя перемен­ными; решение подстановкой и сложением. Примеры решения систем нелинейных уравнений с двумя переменными.

Решение текстовых задач алгебраическим способом.

Декартовы координаты на плоскости. Графическая интер­претация уравнения с двумя переменными. График линейного уравнения с двумя переменными; угловой коэффициент прямой; условие параллельности прямых. Графики простейших нелиней­ных уравнений: парабола, гипербола, окружность. Графическая интерпретация систем уравнений с двумя переменными.

Неравенства. Числовые неравенства и их свойства.

Неравенство с одной переменной. Равносильность нера­венств. Линейные неравенства с одной переменной. Квадрат­ные неравенства. Системы неравенств с одной переменной.

Функции

Основные понятия. Зависимости между величинами. По­нятие функции. Область определения и множество значений функции. Способы задания функции. График функции. Свой­ства функций, их отображение на графике. Примеры графиков зависимостей, отражающих реальные процессы.

Числовые функции. Функции, описывающие прямую и обратную пропорциональные зависимости, их графики и свой­ства. Линейная функция, её график и свойства. Квадратичная функция, её график и свойства. Степенные функции с нату­ральными показателями 2 и 3, их графики и свойства. Графи­ки функций .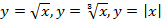

Числовые последовательности. Понятие числовой после­довательности. Задание последовательности рекуррентной фор­мулой и формулой п-го члена.

Арифметическая и геометрическая прогрессии. Формулы п-го члена арифметической и геометрической прогрессий, сум­мы первых п-х членов. Изображение членов арифметической и геометрической прогрессий точками координатной плоско­сти. Линейный и экспоненциальный рост. Сложные проценты.

Вероятность и статистика

Описательная статистика. Представление данных в виде таблиц, диаграмм, графиков. Случайная изменчивость. Ста­тистические характеристики набора данных: среднее арифме­тическое, медиана, наибольшее и наименьшее значения, раз­мах. Представление о выборочном исследовании.

Случайные события и вероятность. Понятие о случай­ном опыте и случайном событии. Частота случайного события.

Статистический подход к понятию вероятности. Вероятности противоположных событий. Независимые события. Умножение вероятностей. Достоверные и невозможные события. Равновоз- можность событий. Классическое определение вероятности.

Комбинаторика. Решение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал.

Логика и множества

Теоретико-множественные понятия. Множество, элемент множества. Задание множеств перечислением элементов, харак­теристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначение. Подмножество. Объединение и пересечение множеств, разность множеств.

Иллюстрация отношений между множествами с помощью диаграмм Эйлера Венна.

Элементы логики. Понятие о равносильности, следовании, употребление логических связок если …, то ..., в том и толь­ко в том случае, логические связки и, или.

Истоки теории вероятностей: страховое дело, азартные игры. П. Ферма и Б. Паскаль. Я. Бернулли. А. Н. Колмогоров

Математика в историческом развитии

История формирования понятия числа: натуральные числа, дроби, недостаточность рациональных чисел для геометриче­ских измерений, иррациональные числа. Старинные системы записи чисел. Дроби в Вавилоне, Египте, Риме. Открытие де­сятичных дробей. Старинные системы мер. Десятичные дроби и метрическая система мер. Появление отрицательных чисел и нуля. Л. Магницкий. Л. Эйлер.

Зарождение алгебры в недрах арифметики. Ал-Хорезми. Рож­дение буквенной символики. П. Ферма, Ф. Виет, Р. Декарт. Исто­рия вопроса о нахождении формул корней алгебраических урав­нений, неразрешимость в радикалах уравнений степени, боль­шей четырёх. Н. Тарталья, Дж. Кардано, Н. X. Абель, Э. Галуа.

Изобретение метода координат, позволяющего переводить геометрические объекты на язык алгебры. Р. Декарт и П. Фер­ма. Примеры различных систем координат на плоскости.

Задача Леонардо Пизанского (Фибоначчи) о кроликах, чис­ла Фибоначчи. Задача о шахматной доске.

Тематическое планирование и виды деятельности учащихся

АЛГЕБРА

7 - 9 классы (306 часов)

Основные виды учебной деятельности

- Чтение формул, правил, теорем, записанных на математическом языке в знаково-символьном виде. Перевод словесных формулировок математических утверждений на математический язык.

- Описание реальных ситуаций с помощью математических моделей: функций, уравнений, неравенств, систем уравнений и неравенств.

- Планирование хода решения задач с использованием трех этапов математического моделирования. Прогнозирование результата решения, оценка реальности полученного ответа.

- Узнавание, построение и описание графических моделей элементарных функций, изучаемых в 7 – 9 классах. Применение графического метода решения уравнений, неравенств, систем уравнений.

- Составление алгоритма построения графика, решения уравнения, неравенства, систем уравнений или неравенств, выполнения алгебраических преобразований.

- Выполнение алгебраических преобразований, пошаговый контроль правильности и полноты выполнения алгоритма преобразования.

- Поиск, обнаружение и устранение ошибок арифметического, алгебраического и логического характера.

- Сравнение разных способов вычислений, преобразований, решений задач, выбор оптимального способа.

- Осуществление исследовательской деятельности: наблюдение, анализ, выявление закономерности, выдвижение гипотезы, доказательство, обобщение результата.

- Вывод формул, доказательство свойств, формулирование утверждений.

- Сбор, анализ, обобщение и представление статистических данных.

- Поиск информации в учебной и справочной литературе и в Интернете.

Планируемые результаты обучения

К концу изучения курса алгебры в основной школе будет обеспечена готовность учащихся к дальнейшему образованию, достигнут необходимый уровень их математического развития:

- осознание возможностей и роли математики в познании и описании реальных ситуаций окружающего мира, понимание математики как части общечеловеческой культуры;

- осознание того, как математически определенные функции описывают реальные процессы и зависимости, умение приводить примеры;

- умение моделировать реальные ситуации;

- понимание того, как потребности практической деятельности человека привели к расширению понятия числа;

- понимание того, как используются математические формулы, уравнения и неравенства; умение приводить примеры их применения для решения математических и практических задач;

- способность понимать существо понятия математического доказательства, алгоритма действия, приводить их примеры;

- способность проводить математическое исследование, анализировать, обобщать, делать выводы;

- применение универсальных учебных действий (анализ, сравнение, обобщение, классификация) для упорядочивания, установления закономерностей на основе математических фактов;

- осознание вероятностного характера многих закономерностей окружающего мира; понимание статистических закономерностей и выводов;

- осуществление поиска необходимой информации в учебной и справочной литературе и в Интернете;

- осуществление проверки хода решения и оценки результата выполнения математического задания, обнаружение и исправление ошибок.

- понимание того, как используются математические формулы, уравнения и неравенства; умение приводить примеры их применения для решения математических и практических задач;

- способность понимать существо понятия математического доказательства, алгоритма действия, приводить их примеры;

- способность проводить математическое исследование, анализировать, обобщать, делать выводы;

- применение универсальных учебных действий (анализ, сравнение, обобщение, классификация) для упорядочивания, установления закономерностей на основе математических фактов;

- осознание вероятностного характера многих закономерностей окружающего мира; понимание статистических закономерностей и выводов;

- осуществление поиска необходимой информации в учебной и справочной литературе и в Интернете;

- осуществление проверки хода решения и оценки результата выполнения математического задания, обнаружение и исправление ошибок.

Планируемые результаты изучения курса «Алгебра» в 7 классе.

-Умение составлять числовые и буквенные выражения, записывать математические свойства, правила, формулы на математическом языке; осуществлять числовые подстановки в алгебраические выражения и формулы и выполнять соответствующие вычисления; выражать из формулы одну переменную через другие; находить область допустимых значений переменных в выражении. Умение распознавать и решать линейные уравнения и уравнения, сводящиеся к ним; решать текстовые задачи алгебраическим методом: описывать реальную ситуацию в виде математической модели – линейного уравнения, решать полученное уравнение и интерпретировать результат. Умение изображать числа и числовые промежутки на координатной прямой, определять принадлежность точки данному числовому промежутку.

-Умение строить на координатной плоскости точки и фигуры по заданным координатам, фигуры, симметричные данным относительно координатных осей и начала координат, а также определять координаты точек, данных на координатной плоскости. Первоначальные умения записывать уравнения прямых, параллельных координатным осям. Понимание, что такое линейное уравнение с двумя переменными. Умение узнавать указанные уравнения, выражать в них одну переменную через другую, определять, является ли пара чисел решением уравнения с двумя переменными. Умение строить прямую, которая является графиком данного линейного уравнения с двумя переменными.

Понимание, что такое линейная функция, что такое независимая переменная – аргумент, зависимая переменная – функция. Знание способов задания функции формулой и графически, умение составлять таблицы значений функции. Умение строить и читать графики линейной функции, находить по графику значение одной переменной по значению другой, определять наименьшее и наибольшее значения функции, решать графически линейные уравнения и неравенства. Умение показывать схематически положение на координатной плоскости графиков функций 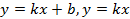_{ } в зависимости от значений коэффициентов k и b.

-Понимание того, что такое система двух линейных уравнений с двумя переменными. Умение узнавать указанные системы, определять, является ли пара чисел решением системы двух линейных уравнений с двумя переменными. Умение решать системы двух линейных уравнений с двумя переменными графическим методом, использовать функционально-графические представления для исследования систем уравнений на предмет числа решений. Умение решать системы двух линейных уравнений с двумя переменными методом подстановки и алгебраического сложения. Умение решать текстовые задачи алгебраическим методом, составляя математическую модель задачи в виде системы двух линейных уравнений с двумя переменными, решать полученную систему и интерпретировать результат.

-Знание определения степени с натуральным показателем и ее свойств, умение вычислять степень числа. Знание табличных значений степеней 2, 3, 5, 10. Понятие степени с нулевым показателем. Умение применять свойства степени для преобразования выражений и вычислений. Умение конструировать математические предложения с помощью связок «если…, то…», воспроизводить несложные доказательства изученных теорем о свойствах степени с натуральным показателем. Умение решать простейшие уравнения, используя определение степени с неотрицательным целым показателем.

-Понимание, что такое одночлен. Умение записывать одночлены в стандартном виде, умение приводить одночлены к стандартному виду. Умение выполнять сложение и вычитание подобных одночленов, умножение одночленов, возведение одночлена в степень, деление одночлена на одночлен в корректных случаях.

- Понимание, что такое многочлен. Умение записывать многочлены в стандартном виде, умение выполнять сложение и вычитание многочленов, умножение многочлена на одночлен, умножение многочлена на многочлен. Умение применять правило умножения многочленов для выведения формул разности квадратов, квадрата двучлена и суммы (разности) кубов. Умение применять формулы сокращенного умножения для преобразования алгебраических выражений. Умение выполнять деление многочлена на одночлен, если такое деление корректно.

-Умение видеть способ, которым данный многочлен можно разложить на множители и выполнять это разложение. Умение применять формулы сокращенного умножения для разложения многочлена на множители. Умение применять разложение многочлена на множители для решения уравнений, сокращения алгебраических дробей, доказательства делимости значения числового выражения на число, а также как способ рациональных вычислений. Понимание, что такое тождество и тождественное преобразование выражений.

- Понятие о функциях 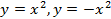_{ }, умение вычислять значения этих функций, составлять таблицы значений функции, строить графики функций и описывать их свойства на основе графических представлений. Умение графически решать уравнения, системы уравнений и простейшие неравенства. Первоначальное умение строить график кусочной функции и проводить на основе графических представлений простейшие исследования. Понятие о функциональной символике, умение находить значение функции, используя функционально-символическую запись, осуществлять подстановку одного выражения в другое. Умение использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями. Умение строить речевые конструкции с использованием функциональной терминологии.

- Умение извлекать информацию из таблиц и диаграмм, выполнять вычисления по табличным данным, организовывать информацию в виде таблиц и диаграмм, приводить примеры числовых данных, находить среднее значение, объем, моду, размах.

Планируемые результаты изучения курса «Алгебра» в 8 классе.

-Представление о допустимых значениях алгебраической дроби и умение их находить. Знание основного свойства алгебраической дроби и умение применять его для преобразования дробей; умение выполнять действия с алгебраическими дробями, доказывать тождества. Понятие степени с целым показателем, умение вычислять значения степеней с отрицательным показателем, иллюстрировать примерами свойства степени с целым показателем. Первичные представления о рациональных уравнениях, методах их решения, отборе корней

-Систематизация знания о рациональных числах, понятия иррационального числа, множества действительных чисел. Умение находить приближения рациональных и иррациональных чисел, сравнивать и упорядочивать действительные числа. Освоение понятие квадратного корня из неотрицательного числа, умение строить график функции 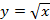_{ }, описывать ее свойства, использовать график для нахождения квадратных корней и оценки их приближенных значений, вычислять квадратные корни с помощью калькулятора. Умение исследовать и доказывать свойства квадратных корней, применять их для преобразования выражений. Освоение понятие модуля действительного числа, функции 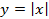_{ }, умение строить ее график и описывать свойства, умение строить графики кусочных функций, описывать их свойства на основе графических представлений, использовать функциональную символику, строить речевые конструкции с использованием функциональной терминологии.

-Умение вычислять значения функций, заданных формулами, составлять таблицы значений функции, распознавать виды изучаемых функций, строить графики, описывать свойства функций, осуществлять параллельный перенос графика функции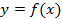_{ }на координатной плоскости. Умение использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями; использовать функционально-графические представления для решения и исследования уравнений, решения систем уравнений и неравенств.

-Освоение понятия квадратного уравнения, умение распознавать квадратные уравнения, проводить исследование на предмет количества корней квадратного уравнения по дискриминанту и коэффициентам, умение применять формулы корней для решения квадратных уравнений. Умение решать рациональные уравнения и уравнения, сводящиеся к квадратным, умение решать текстовые задачи алгебраическим методом: составлять математическую модель – квадратное либо рациональное уравнение, решать его и интерпретировать результат.

-Знание свойств числовых неравенств, умение иллюстрировать их на координатной прямой, применять при исследовании функции на монотонность, доказательстве и решении неравенств. Умение распознавать линейные и квадратные неравенства, решать их, показывать решение неравенства в виде числового промежутка на числовой прямой. Умение находить приближенные значение числа с недостатком и с избытком, умение прикидывать и примерно оценивать результат. Умение представлять числа в стандартном виде и выполнять арифметические действия с числами, записанными в стандартном виде, использовать запись числа в стандартном виде для выражения размеров объектов, длительности процессов в реальном мире, сравнивать числа, записанные в стандартном виде.

-Ознакомление с основными методами решения простейших комбинаторных задач: перебор вариантов, построение дерева вариантов, правило умножения. Умение применять правило комбинаторного умножения для решения задач на нахождение числа объектов или комбинаций.

Планируемые результаты изучения курса «Алгебра» в 9 классе.

- Умение распознавать виды неравенств: линейное, квадратное, рациональное, и выбирать способ решения. Освоение различных методов решения и систем неравенств. Умение строить геометрическую модель решения неравенства и систем неравенств. Умение интерпретировать результат.

Освоение понятий множество, элемент множества, пустое множество, подмножество, объединение и пересечение множеств. Умение показывать объединение и пересечение множеств с помощью кругов Эйлера, на числовой прямой и координатной плоскости.

- Знание уравнений окружности, прямой, параболы, гиперболы, уравнений с модулем.

Умение применять в решении систем уравнений графические и аналитические методы. Умение выполнять преобразование уравнений, входящих в систему, вводить новую переменную, интерпретировать и оценивать результат.

Умение применять системы уравнений в решении задач. Освоение приемов решения задач на производительность труда.

Умение проводить анализ и графическое исследование решения систем уравнений, в том числе с уравнением окружности, делать выводы и интерпретировать результат исследования.

- Умение вычислять значения функций, заданных формулами, составлять таблицы значений функции, распознавать виды изучаемых функций, способы их задания, строить графики, описывать свойства функций, осуществлять параллельный перенос графика функции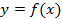_{ }на координатной плоскости. Умение использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями; использовать функционально-графические представления для решения и исследования уравнений, решения систем уравнений и неравенств. Умение находить решение в проблемной ситуации.

- Ознакомление с новой математической моделью – числовая последовательность, арифметическая и геометрическая прогрессии, способами задания последовательностей, формуламиn-го члена, графиками числовых последовательностей. Знание формул n-го члена, суммы членов конечной арифметической и геометрической прогрессии, характеристических свойств. Освоение новой терминологии, новых символов и обозначений. Умение распознавать арифметическую и геометрическую прогрессии, находить неизвестный компонент формулы n-го члена, формулы суммы конечной арифметической или геометрической прогрессии, применять характеристическое свойство прогрессии. Знание формулы сложных процентов. Умение производить несложные расчеты процентов банковских операций. Умение моделировать реальные ситуации с помощью последовательностей.

- Умение применять основные методы решения комбинаторных задач: перебор вариантов, построение дерева вариантов, правило умножения. Умение применять правило комбинаторного умножения для решения задач на нахождение числа объектов или комбинаций.

Освоение понятия факториал, умение применять определение факториала в решении комбинаторных задач.

Ознакомление с новой математической моделью – классической вероятностной схемой и формулой для подсчета вероятности.

Знание основных видов случайных событий: достоверные, невозможные, несовместные события, события, противоположные данным; сумма двух случайных событий. Умение проводить доказательство формул и теорем.

Знание числовых характеристик информации, полученной в результате эксперимента. Умение проводить эксперимент. Умение использовать методы статистической обработки результатов измерений, полученных при проведении эксперимента. Умение группировать данные, проводить обработку данных, представлять информацию в виде таблиц, диаграмм, гистограмм, графиков.

VII. Планируемые результаты изучения учебного предмета АЛГЕБРА.

Рациональные числа

Выпускник научится:

1. понимать особенности десятичной системы счисления;

2. владеть понятиями, связанными с делимостью натураль­ных чисел;

3. выражать числа в эквивалентных формах, выбирая наи­более подходящую в зависимости от конкретной ситуации;

4. сравнивать и упорядочивать рациональные числа;

5. выполнять вычисления с рациональными числами, со­четая устные и письменные приёмы вычислений, применять калькулятор;

6. использовать понятия и умения, связанные с пропорци­ональностью величин, процентами в ходе решения математи­ческих задач и задач из смежных предметов, выполнять не­сложные практические расчёты.

Действительные числа

Выпускник научится:

1. использовать начальные представления о множестве дей­ствительных чисел;

2. владеть понятием квадратного корня, применять его в вычислениях.

Измерения, приближения, оценка

Выпускник научится:

1) использовать в ходе решения задач элементарные пред­ставления, связанные с приближёнными значениями величин.

Выпускник научится:

1. владеть понятиями «тождество», «тождественное преоб­разование», решать задачи, содержащие буквенные данные; ра­ботать с формулами;

2. выполнять преобразования выражений, содержащих сте­пени с целыми показателями и квадратные корни;

3. выполнять тождественные преобразования рациональ­ных выражений на основе правил действий над многочленами и алгебраическими дробями;

4. выполнять разложение многочленов на множители.

Уравнения

Выпускник научится:

1. решать основные виды рациональных уравнений с одной переменной, системы двух уравнений с двумя переменными;

2. понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных си­туаций, решать текстовые задачи алгебраическим методом;

3. применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.

4. применять графические представления для исследова­ния уравнений, систем уравнений, содержащих буквенные коэффициенты.

Неравенства

Выпускник научится:

1. понимать и применять терминологию и символику, свя­занные с отношением неравенства, свойства числовых нера­венств;

2. решать линейные неравенства с одной переменной и их системы; решать квадратные неравенства с опорой на графи­ческие представления;

3. применять аппарат неравенств для решения задач из раз­личных разделов курса.

Основные понятия. Числовые функции.

Выпускник научится:

1. понимать и использовать функциональные понятия и язык (термины, символические обозначения);

2. строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;

3)понимать функцию как важнейшую математическую мо­дель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследова­ния зависимостей между физическими величинами.

Числовые последовательности

Выпускник научится:

1. понимать и использовать язык последовательностей (тер­мины, символические обозначения);

2. применять формулы, связанные с арифметической и гео­метрической прогрессиями, и аппарат, сформированный при изучении других разделов курса, к решению задач, в том числе с контекстом из реальной жизни.

Описательная статистика

Выпускник научится использовать простейшие способы представления и анализа статистических данных.

Случайные события и вероятность

Выпускник научится находить относительную частоту и ве­роятность случайного события.

Комбинаторика

Выпускник научится решать комбинаторные задачи на на­хождение числа объектов или комбинаций.

19