Муниципальное Автономное Общеобразовательное Учреждение "Лицей № 6"
Банковские задачи
Выполнили: Чиканова Анастасия и Терехов Илья,
ученики 10А класса.
Руководитель: Мухометзянова Любовь Васильевна,
учитель высшей квалификационной категории.
Бердск 2016
План:
Введение (стр. 3)
1.1. Обоснование выбора темы. (стр. 3)
1.2. Цель и задачи работы. (стр. 3)
2. Разновидности задачи №17 из ЕГЭ. (стр. 4)
3.Банковские проценты. (стр. 4-7)
3.1 Простые проценты. (стр. 4-6)
3.2. Сложные проценты. (стр. 6-7)
4.Банковские задачи. (стр. 7-15)
4.1 Нахождение ежегодного платежа. (стр. 7-10)
4.2. Нахождение суммы кредита. (стр. 10-12)
4.3. Вычисление процентной ставки по кредиту. (стр. 12-13)
4.4. Нахождение количества лет выплаты кредита. (стр. 13-15)
5. Задачи на кредиты дифференцированных платежей. (стр. 15-17)
6. Заключение. (стр. 18)
1. Введение
Обоснование выбора темы:
Понимание процентов и умение производить процентные расчеты в настоящее время необходимо каждому человеку: прикладное значение этой темы очень велико и затрагивает финансовую, демографическую, экологическую, социологическую и другие стороны нашей жизни. Актуальность исследования очевидна.
Исследовательская работа направлена на развитие коммуникативных способностей, самостоятельности; способности на основе полученных сведений и теоретических знаний создавать новые продукты на основе умений находить, анализировать, обрабатывать, интегрировать, оценивать и создавать информацию в разных формах и на различных типах медиа оборудования. Данная исследовательская работа способствует саморазвитию и проявлению индивидуальности.
1.2.
Цель работы:
Научиться решать задачи экономического содержания из ЕГЭ. Рассмотреть способы решения таких задач.
Знать методику решения таких задач.
Задачи:
изучить литературу по данной теме;
решать задачи на каждый из типов банковских задач
2. Разновидности задачи №17 из ЕГЭ
Задачи №17 из ЕГЭ по математике (профильный уровень) – это текстовые задачи экономического содержания, в которых усилена практическая составляющая условия. Данные задачи можно разделить на два типа: Задачи, использующие дискретные модели (проценты, кредиты, вклады, вклады с пополнением и др.), и задачи, использующие непрерывные модели (производство, объемы выпускаемой продукции, протяженные во времени и др.). В любом случае данные задачи требуют построения математической модели, введения переменных и решения составленных уравнений, или систем уравнений.
В данном докладе мы будем рассматривать только задачи на сложные банковские проценты.
3. Банковские проценты
3.1. Простые проценты
В реальной экономической деятельности проценты используются в сфере банковских расчетов. С одной стороны банки принимают вклады и платят по этим вкладам проценты вкладчикам, а с другой стороны, - выдают кредиты заемщикам и получают от них проценты за пользование деньгами. Разность между суммой, которую получает банк от заемщика за предоставленные кредиты, и той, которую он выплачивает по вкладам, и составляет прибыль банка.
Проценты могут рассчитываться по- разному в зависимости от вида, характера и срока вклада. Проценты определяются в виде некоторой доли от величины вклада, и начисляются один раз за определенный период, называемый периодом начисления процентов. Периодом начисления процентов не обязательно является год, может быть и полгода, месяц, день.
В зависимости от способа начисления процентов (от выбора базы начисления) выделяют два вида процентов: простые и сложные.
Увеличение суммы вклада 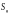 по методу простых процентов характеризуется тем, что в течение всего срока хранения вклада проценты начисляются только на первоначальную сумму вклада
по методу простых процентов характеризуется тем, что в течение всего срока хранения вклада проценты начисляются только на первоначальную сумму вклада 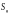 независимо от срока хранения и количества периодов начисления процентов.
независимо от срока хранения и количества периодов начисления процентов.
Увеличение суммы вклада 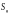 по методу сложных процентов характеризуется тем, что в течение срока хранения вклада проценты начисляются не только на первоначальную сумму вклада
по методу сложных процентов характеризуется тем, что в течение срока хранения вклада проценты начисляются не только на первоначальную сумму вклада 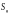 но и на сумму начисленных процентов за прошедшие периоды( т.е. начисляются на всю сумму денег на счете вкладчика) .
но и на сумму начисленных процентов за прошедшие периоды( т.е. начисляются на всю сумму денег на счете вкладчика) .
Введем следующие условные обозначения: 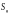 - первоначальная сумма вклада, i – ставка банковского процента, n- количество периодов начисления процентов,
- первоначальная сумма вклада, i – ставка банковского процента, n- количество периодов начисления процентов, 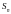 - сумма вклада через n –периодов.
- сумма вклада через n –периодов.
Предположим сначала, что банк выплачивает проценты по вкладам, используя метод простых процентов. Пусть вкладчик открыл сберегательный счет и положил на него
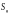 рублей, а банк обязуется выплачивать вкладчику в конце каждого года i % от первоначальной суммы вклада. Тогда по истечении первого года сумма начисленных банком процентов составит
рублей, а банк обязуется выплачивать вкладчику в конце каждого года i % от первоначальной суммы вклада. Тогда по истечении первого года сумма начисленных банком процентов составит 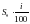 рублей, а величина вклада станет равной :
рублей, а величина вклада станет равной :
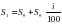 .
.
Поскольку банк начисляет проценты только на первоначальную суммы(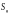 ), то по прошествии второго года на счете вкладчика окажется:
), то по прошествии второго года на счете вкладчика окажется:
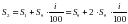
Таким образом , на величину 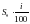 банк никаких начислений не производит ( т.е. банк бесплатно использует эти деньги)
банк никаких начислений не производит ( т.е. банк бесплатно использует эти деньги)
Через n –периодов сумма начисленных процентов составит 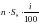 , а величина средств, лежащих на счете вкладчика , будет равняться:
, а величина средств, лежащих на счете вкладчика , будет равняться:
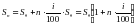 (формула простых процентов)
(формула простых процентов)
В формуле задействованы четыре переменные ( 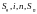 ), поэтому можно рассмотреть четыре типа задач, основанных на ее использовании ( в каждом из них по трем известным переменных мы можем найти четвертую)
), поэтому можно рассмотреть четыре типа задач, основанных на ее использовании ( в каждом из них по трем известным переменных мы можем найти четвертую)
3.2 Начисление банком простых процентов - не очень справедливый способ расчета с вкладчиком. Если вкладчик не будет регулярно снимать сумму начисленных процентов со счета, то он оказывается в невыгодном положении, поскольку банк бесплатно пользуется его деньгами, и эта несправедливость будет только возрастать. Наиболее справедливо выплачивать проценты по вкладам по методу сложных процентов. В этом случае , если вкладчик не снимает со счета сумму начисленных процентов, то эта сумма присоединяется к основному вкладу, а в конце следующего периода банк начисляет проценты уж на новую , увеличенную сумму( т.е. проценты начисляются не только на основной вклад 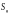 , но и на проценты , которые были начислены за прошедшие периоды)
, но и на проценты , которые были начислены за прошедшие периоды)
Выведем формулу для расчета сложных процентов. Пусть вкладчик открыл сберегательный счет и положил на него 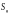 рублей сроком на n – лет, а ставка банковского процента составляет i% от суммы вклада на текущий период. Тогда по истечении первого года сумма начисленных банком процентов составит
рублей сроком на n – лет, а ставка банковского процента составляет i% от суммы вклада на текущий период. Тогда по истечении первого года сумма начисленных банком процентов составит 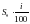 рублей и на счете вкладчика будет
рублей и на счете вкладчика будет 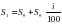 рублей. По прошествии второго года банк начислит i% уже на сумму
рублей. По прошествии второго года банк начислит i% уже на сумму 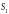 рублей и поэтому она увеличится на
рублей и поэтому она увеличится на 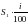 , а в конце второго года на счете окажется
, а в конце второго года на счете окажется 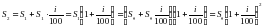 рублей. В конце третьего года банк начисляет i% уже на сумму
рублей. В конце третьего года банк начисляет i% уже на сумму 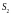 рублей, а поэтому в конце года на счете вкладчика будет лежать уже
рублей, а поэтому в конце года на счете вкладчика будет лежать уже 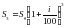 . Итак, по прошествии n –лет сумма денег на счете вкладчика достигает величины:
. Итак, по прошествии n –лет сумма денег на счете вкладчика достигает величины:
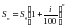 (формула сложных процентов)
(формула сложных процентов)
Рост первоначальной суммы вклада по методу сложных процентов - это процесс, развивающийся по законам геометрической прогрессии, первый член которой равен 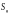 , а знаменатель равен
, а знаменатель равен  . Аналогично случаю простых процентов, также можно сформулировать четыре типа задач, позволяющих по трем данным характеристикам найти четвертую. В настоящее время расчет по методу сложных процентов является преобладающим.
. Аналогично случаю простых процентов, также можно сформулировать четыре типа задач, позволяющих по трем данным характеристикам найти четвертую. В настоящее время расчет по методу сложных процентов является преобладающим.
4.Решение банковских задач
4.1. Нахождение ежегодного платежа.
Начнем решать задачи на кредиты, проценты из демонстративного варианта КИМ для ЕГЭ 2016 года по математике (профильный уровень):
Условие задачи: 31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
Решение:
Сумма кредита – 9.930.000 рублей
Ежегодный платеж - х рублей
Проценты - 10% годовых
1 способ решения.
Пусть х- один из трехразовых платежей.
Тогда сумма долга после оплаты в первом году составит: (9.930.000*1,1 -х)
После внесения второго платежа сумма долга станет равной:
(9.930.000*1,1-х) *1,1-х
Аналогично, сумма долга после третьего платежа:
((9.930.000*1,1-х) *1,1-х) *1,1-х
Третьим платежом Сергей должен погасить долг, то есть долг станет равен нулю. Из этого следует:
((9.930.000*1,1-х) *1,1-х) *1,1-х=0
Решая уравнение, получаем, что х= 3.993.000
Ответ: 3.993.000 руб.
2 способ решения
Выведем формулу для решения подобных задач на кредиты.
Пусть сумма кредита =a на 31 декабря 2013 г.
Ежегодный платеж равен - х,
Годовой процент k%.
Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент m = 1 +  = 1 + 0,01k
= 1 + 0,01k
31 декабря 2014 г. (после первой выплаты) сумма долга составит:

31 декабря 2015 г. (после второй выплаты) сумма долга составит : 
31 декабря 2016 г. (после третьей выплаты) сумма долга составит : 
Найдем сумму  . Это сумма трех членов геометрической прогрессии , в которой первый член равен 1, а знаменатель прогрессии равен m .
. Это сумма трех членов геометрической прогрессии , в которой первый член равен 1, а знаменатель прогрессии равен m .  .
.  .
.
Тогда сумма долга после третьей выплаты составит: и она равна нулю, т.к. Сергей должен погасить кредит полностью.
и она равна нулю, т.к. Сергей должен погасить кредит полностью.
Составим уравнение:

 (*)
(*)
В этой формуле : а – кредит, m- коэффициент, полученный из годового процента k : m = 1 +  = 1 + 0,01k, х – платеж.
= 1 + 0,01k, х – платеж.
Из формулы (*) : 
При а= 9 930 000 и k = 10%, получаем m = 1,1 и
Ответ: 3 993 000 рублей.
 Данную формулу перепишем в другом виде:
Данную формулу перепишем в другом виде:
 , в этой формуле %
, в этой формуле %  1+
1+
Таким образом, в данной работе мы будем рассматривать 4 типа задач на проценты:
Нахождение ежегодного платежа.
Нахождение суммы кредита.
Вычисление процентной ставки по кредиту.
Нахождение количества лет выплаты кредита
Задача 2. 31 декабря 2014 года Роман взял в банке 8599000 рублей в кредит под 14% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14%), затем Роман переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Роман выплатил долг тремя равными платежами (т.е. за 3 года)?
Решение:
Для удобства возьмем сумму кредита 8599000 = а, тогда сумма долга после каждой выплаты равна:
2015 г. – а (0,14+1) – х
2016 г. – (а (0,14 +1) – х)1,14 –х
2017 г. – ((1,14а – х)1,14 – х)1,14 – х
После последней выплаты сумма долга стала равна нулю.
Составим уравнение:
((1,14а – х)1,14 – х)1,14 – х = 0
(0,1596а + 1,14 а -1,14 х – х)1,14 –х = 0
0,181944а + 1,2996а – 1,2996х – 1,14х – х = 0
3,4396х = 1,481544 * 8599000
х = 3703860
Ответ: 3703860 рублей.
4.2. Нахождение суммы кредита:
Задача 1. 31 декабря 2014 года Ярослав взял в банке некоторую сумму в кредит под 12,5% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Ярослав переводит в банк 2 132 325 рублей. Какую сумму взял Ярослав в банке, если он выплатил долг четырьмя равными платежами (то есть за четыре года)?
Решение.
Заметим сначала, что увеличить число на 12,5, это тоже самое, что и умножить это число на 9/8. Пусть Ярослав взял в банке N рублей, а его ежегодный платеж равен a (в данном случае а=2.132.325). Тогда из условия следует уравнение: (((9/8N-a) *9/8-a) *9/8-a) *9/8-a
Решая это уравнение, получаем: N= 64090000
Ответ: 6409000 рублей
Задача 2. 31декабря 2014 года Максим взял в банке некоторую сумму денег в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем Максим переводит в банк 2928200 рублей. Какую сумму взял Максим в банке, если он выплатил долг четырьмя равными платежами, то есть за 4 года?
Решение:
Пусть сумма кредита = х, а сумма ежегодного платежа 2928200 = а (для удобства расчетов), тогда распишем сумму долга для каждого года:
2014 г. – х (руб.)
2015 г. – х (0,1 +1) –а
2016 г. – (1,1х –а) (0,1+1) – а
2017 г. – ((1,1х – а) (0,1 + 1) –а) 1,1 – а
2018 г. (((1,1х – а)1,1 –а)1,1 - а)1,1 – а
После последней выплаты сумма долга стала равна нулю.
Составим уравнение:
(((1,1х – а)1,1 –а)1,1 – а)1,1 – а = 0
((1,21х – 2,1 а) 1,1-а)1,1 – а =0
(1,331х – 3,31а)1,1 –а = 0
1, 4641х - 4,641а = 0
1, 4641х = 4,641* 2928200
х = 9282000
Ответ: 9282000 рублей.
4.3. Нахождение процентной ставки по кредиту
Условие задачи:
Фермер получил кредит в банке под определенный процент годовых. Через год фермер в счет погашения кредита вернул в банк 3/4 от всей суммы, которую он должен банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму, на 21% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?
Решение:
Пусть сумма кредита составляет S, а процентная ставка по кредиту- x%.
К концу первого года сумма долга фермера в банк с учетом начисленных процентов составила (1+0,01х) S
После возвращения банку 3/4 части от суммы долга долг фермера на следующий год составил 1/4(1+0,01х) S
На эту сумму в следующем году вновь начислены проценты. Сумма долга фермера к концу второго года погашения кредита с учетом процентной ставки составила 1/4(1+0,01х) ^2*S. По условию задачи эта сумма равна 1,21S (Т.к. Сумма увеличена на 21%)
Решим уравнение: 1/4(1+0,01х)^2*S= 1,21S
В ответ мы можем брать только положительные сила, тогда:
1+0,01х=1,1*2
0,01х=1,2
х=120
Ответ: 120
Задача 2. 31 декабря 2014 года Валерий взял в банке 1000000 рублей в кредит. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем Валерий переводит в банк очередной транш. Валерий выплатил кредит за 2 транша. В первый раз Валерий перевел в банк 660000 рублей, во второй – 484000 рублей. Под какой процент банк выдал кредит Валерию?
Решение:
Пусть 1000000 = а (для удобства в расчетах), тогда сумма долга после выплаты очередного транша будет равна:
2015 г. – а (0,01х +1) – 660000
2016 г. – (а (0,01х +1) – 660000)(0,01х +1) – 484000
После выплаты второго транша сумма долга стала равна нулю.
Составим уравнение:
(а(0,01х+1) – 660000)(0,01х + 1) – 484000 = 0
(0,01ах + а – 660000)(0,01х +1) – 484000 = 0
(10000х + 340000)(0,01х + 1) -484000 = 0
100х^2 +10000х +3400х +340000 – 484000 = 0/ :100
х^2 +134х – 1440 = 0
D = 23716 = 154^2
X1 = 10
X2 = -144 - не удовлетворяет условие задачи
10 (%) годовых –процент, под который Валерий взял кредит в банке
Ответ: 10%
4.4. Нахождение количества лет выплаты кредита
Условие задачи:
1 января 2015 года Тарас Павлович взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая — 1 числа каждого следующего месяца банк начисляет 2 процента на оставшуюся сумму долга (то есть увеличивает долг на 2%), затем Тарас Павлович переводит в банк платёж. На какое минимальное количество месяцев Тарас Павлович может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?
Решение:
Срок кредита будет минимален в том случае, когда выплаты составляют 220 тыс. рублей. Составим таблицу, в первом столбце которой будем указывать долг на первое число месяца, а во втором — долг в том же месяце, но уже после выплаты. Для упрощения расчётов будем сохранять только два знака после запятой, представляя суммы долга в тыс. рублей.
Формула суммы оставшегося долга: сумма кредита *(0,01 процентная ставка +1) – ежегодный транш.
| Месяц | Долг на первое число месяца (тыс. руб.)
| Долг после выплаты (тыс. руб.)
|
| 1 | 1122 | 902 |
| 2 | 920,04 | 700,04 |
| 3 | 714,04 | 494,04 |
| 4 | 503,92 | 283,92 |
| 5 | 289,60 | 69,60 |
| 6 | 70,99 | 0 |
Заметим, что в последний месяц выплата составит менее 220 тыс. руб. Из таблицы видно, что минимальный срок кредита в условиях задачи составляет 6 месяцев.
Ответ: 6 месяцев
Задача 2
Условие задачи:
Савелий хочет взять в кредит 1,4 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Савелий взять кредит, чтобы ежегодные выплаты были не более 330 тысяч рублей?
Решение:
Срок кредита будет минимален в том случае, когда выплаты составляют 330 тыс. рублей. Составим таблицу, в первом столбце которой будем указывать долг после начисления процентов, а во втором — долг после выплаты. Для упрощения расчётов будем сохранять только два знака после запятой, представляя суммы долга в тыс. рублей.
Формула суммы оставшегося долга: сумма кредита *(0,01 процентная ставка +1) – ежегодный транш.
| Год | Долг до выплаты (тыс. руб.) | Долг после выплаты (тыс. руб.) |
| 1 | 1540 | 1210 |
| 2 | 1331 | 1001 |
| 3 | 1101,1 | 771,1 |
| 4 | 848,21 | 518,21 |
| 5 | 570,3 | 240,03 |
| 6 | 254,03 | 0 |
Ответ: 6 лет
5.Задачи на кредиты дифференцированных платежей.
Задачи на кредиты с отдачей по схеме дифференцированных платежей – сумма долга уменьшается равномерно на одну и ту же величину. Отдача производится платежами , каждый из которых состоит из двух частей: проценты на оставшуюся сумму долга и одинаковая часть для каждого платежа , на которую уменьшается сумма долга.
Условие:
В июле планируется взять кредит 200000000 рублей на некоторый срок (целое число лет). Условия возврата таковы:
- каждый январь долг возрастает на 12% по сравнению с концом предыдущего года;
- с февраля по июль каждого года необходимо выплатить часть долга, в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года( )
)
На сколько лет был взят кредит, если известна общая сумма выплат после его погашения равнялась 45,2 млн. руб.?
Решение:
Т.. долг должен быть меньше долга на предыдущий период времени на одну и ту же величину, то платежи не будут равными, потому что в каждый из платежей необходимо выплатить все проценты, начисленные банком до того, и еще часть суммы самого кредита
Поэтому при такой схеме, первый платеж будет самым крупным (проценты начисляются на полную сумму кредита), а последний самым маленьким
Каждый следующий платеж становился все меньше и меньше, т.к. с каждым платежом долг уменьшался на одну и ту же величину, и процент, следовательно, тоже
Пусть S- кредит (20000000)
Сначала банк начисляет процент на всю сумму  ( i=12%- годовой процент)
( i=12%- годовой процент)
В первый же платеж мы выплатим весь процент и долг: 
Тогда основной долг через год будет равен
1 год: S-S/n=S(n-1)/n и уже на эту сумму банк нам начисляет проценты
И т.д. выплачиваем проценты и часть долга, банк начисляет процент на оставшуюся часть.
В результате мы выплатим весь долг S и всю сумму процентов, итого получается 45,2-20=25,2(млн.руб.) – общая сумма начисленных процентов
1 год – 
2 год - 
3 год -
4 год - 
п- лет
Сумма процентов:

Сумма арифметической прогрессии, у которой:



Выведем формулу: 
 ;
;  ;
;  ;
; 
Ответ: 20 лет
6.Заключение
Изучая литературу по данной теме мы:
Рассмотрели понятие процента
Научились решать задачи с экономическим содержанием из ЕГЭ
Рассмотрели все типы задач и на проценты и решали задачи на каждый из типов
Рассмотрели поняли необходимость процентов для обычных жизненных ситуаций, когда люди приходят в банк и берут кредиты.
Список используемой литературы:
1.Высшая математика для экономистов: Учебник для вузов/Н.Ш. Кремер, Б.А.Путко, И.М.Тришин, М.Н.Фридман; Под ред.проф.Кремера.-2-е изд., и перераб. и доп.-М.: ЮНИТИ, 2003.- 471 с.
2. http://alexlarin.net/ege16.html
3. http://www.fipi.ru/about/news/publikaciya-proektov-demoversiy-kim-ege-i-oge-2016-goda







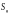 по методу простых процентов характеризуется тем, что в течение всего срока хранения вклада проценты начисляются только на первоначальную сумму вклада
по методу простых процентов характеризуется тем, что в течение всего срока хранения вклада проценты начисляются только на первоначальную сумму вклада 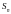 - сумма вклада через n –периодов.
- сумма вклада через n –периодов.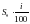 рублей, а величина вклада станет равной :
рублей, а величина вклада станет равной : 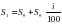 .
.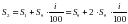
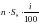 , а величина средств, лежащих на счете вкладчика , будет равняться:
, а величина средств, лежащих на счете вкладчика , будет равняться: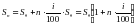 (формула простых процентов)
(формула простых процентов)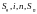 ), поэтому можно рассмотреть четыре типа задач, основанных на ее использовании ( в каждом из них по трем известным переменных мы можем найти четвертую)
), поэтому можно рассмотреть четыре типа задач, основанных на ее использовании ( в каждом из них по трем известным переменных мы можем найти четвертую)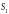 рублей и поэтому она увеличится на
рублей и поэтому она увеличится на 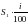 , а в конце второго года на счете окажется
, а в конце второго года на счете окажется 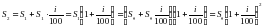 рублей. В конце третьего года банк начисляет i% уже на сумму
рублей. В конце третьего года банк начисляет i% уже на сумму 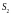 рублей, а поэтому в конце года на счете вкладчика будет лежать уже
рублей, а поэтому в конце года на счете вкладчика будет лежать уже 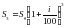 . Итак, по прошествии n –лет сумма денег на счете вкладчика достигает величины:
. Итак, по прошествии n –лет сумма денег на счете вкладчика достигает величины: 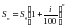 (формула сложных процентов)
(формула сложных процентов)









