«Бенефис одной задачи»

«Бенефис одной задачи»

мастер-класс

Афанасьева Людмила Николаевна-учитель математики первой квалификационной категории МБОУ «Лицей №9 имени А.С.Пушкина ЗМР РТ»

Цель мастер-класса:

Приоритетным в постановке целей является анализ способов решения одной задачи, формирование у школьников навыков исследовательской деятельности, активное вовлечение учащихся в образовательный процесс.

• Решение математических задач разными способами представляет большие возможности для формирования интеллектуальных качеств личности, развивает исследовательские способности учащихся

• Успешность обучения школьников обусловлена сформированностью таких качеств мышления, как гибкость, глубина, целенаправленность, обобщенность, критичность.

Структура урока

• Организационный момент.
• Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
• Актуализация опорных знаний и их коррекция.
• Применение знаний, обобщение и систематизация при решении задач.
• Самоконтроль и коррекция знаний.
• Применение знаний для поиска специальных приемов решения задач (работа в группах)
• Защита мини-проектов.
• Информация о домашнем задании.
• Рефлексия

«Дорога та, что сам искал, вовек не позабудется!»

Задача. В равнобедренном прямоугольном треугольнике ABC (  C=90  ) проведены медиана BD и отрезок CM  BD(точка M принадлежит стороне AB). Найдите отношение AM:BM.

• I группа (в решении используются векторы, координаты)
• II группа ( в решении используется тригонометрия)
• III группа ( в решении применяется равенство треугольников или подобие треугольников)
• IV группа ( в решении используется поворот вокруг точки)
• V группа( в решении используется специальные формулы и теоремы)
• VI группа(в решении используются свойства замечательных линий в треугольнике: высот, медиан, биссектрис)
• VII группа (в решении используются свойства площади)

Это полезно знать!

• Отношение площадей двух треугольников с общей высотой равно отношению длин оснований треугольников, к которым она проведена.

• В прямоугольном треугольнике отношение отрезков гипотенузы, на которые она делится высотой, проведенной из вершины прямого угла, равно отношению квадратов катетов.

• Точка C, делящая отрезок с концами в точках A и B в отношении  -1, имеет координаты

4. Если некоторая прямая отсекает на осях Ox и Oy отрезки с длинами a и b соответственно, то уравнение этой прямой имеет вид

5.Векторы и перпендикулярны тогда и только тогда, когда

6.Теорема Менелая. Если точки заданы на сторонах ВС, АС, АВ треугольника АВС или на продолжениях (рис. 1), то эти точки принадлежат одной прямой тогда и только тогда, когда выполняется соотношение

Рефлексия

• «Сегодня я узнал…»
• «Было интересно…»
• «Было трудно…»
• «Я понял, что…»
• «Теперь я могу…»
• «Я научился…»
• «У меня получилось…»
• «Меня удивило…»
• «Мне захотелось…»

Спасибо за урок!

«Продукт» урока одной задачи

Как показывает опыт, решение одной задачи разными способами эффективнее, чем решение нескольких задач одним способом, поскольку способствует более глубокому пониманию и усвоению материала и формированию у школьников взгляда на математику как на цельную науку. Как можно организовать работу над одной задачей при изучении курса планиметрии?

Большинство геометрических задач допускает решение несколькими способами. Однако на практике возможности того или иного способа решения нередко связывают с задачами определенного типа, что не позволяет оценить в полной мере достоинства и недостатки данного способа. В то же время демонстрация различных способов решения одной задачи дает возможность сравнить последние и выделить преимущества каждого из них. Систематическое применение этого дидактического приема усиливает мотивацию учении и побуждает учащихся искать наиболее простые решения из всех существующих.

В качестве примера рассмотрим следующую геометрическую задачу.

Задача. В равнобедренном прямоугольном треугольнике ABC (  C=90  ) проведены медиана BD и отрезок CM  BD(точка M принадлежит стороне AB). Найдите отношение AM:BM.

Приведем 25 способов решения данной задачи. Но сначала перечислим некоторые использующиеся в них утверждения.

• Отношение площадей двух треугольников с общей высотой равно отношению длин оснований треугольников, к которым она проведена.

• В прямоугольном треугольнике отношение отрезков гипотенузы, на которые она делится высотой, проведенной из вершины прямого угла, равно отношению квадратов катетов.

• Точка C, делящая отрезок с концами в точках A и B в отношении   -1, имеет координаты

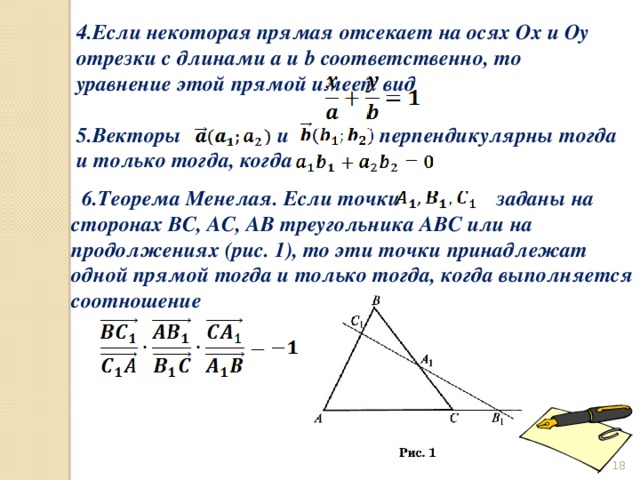
6.Теорема Менелая. Если точки заданы на сторонах ВС, АС, АВ треугольника АВС или на продолжениях (рис. 1), то эти точки принадлежат одной прямой тогда и только тогда, когда выполняется соотношение

4.Если некоторая прямая отсекает на осях Ox и Oy отрезки с длинами a и b соответственно, то уравнение этой прямой имеет вид

5.Векторы и перпендикулярны тогда и только тогда, когда

7. Прямая, проходящая через начало координат и имеющая угловой коэффициент k, задаётся уравнением y = kx.

8. Для четырёхугольника ABCD с взаимно перпендикулярными диагоналями выполняется соотношение

Для удобства пользования разобьём все способы решения на семь групп.

I группа (в решении используются векторы, координаты)

1-й способ.

Введём прямоугольную систему координат так, чтобы вершины

треугольника ABC имели координаты: С(0; 0), А(1; 0), В(0; 1), тогда D (рис.2).

Проведём отрезок . Так как (как углы с взаимно перпендикулярными сторонами), то треугольники BCD и CNM подобны,

следовательно . Пользуясь утверждениями 7 и 4, запишем уравнения прямых СM и и .

Решив систему этих уравнений, найдём координаты

точки пересечения прямых СM и AB: M .

Тогда N и AN = AC – CN = . Так MN || BC,

то

2-й способ. Введём векторы: , .Пусть (рис. 3).

Выразим вектор двумя способами:

откуда . Далее получим:

По условию задачи или , откуда, учитывая, что и , находим . Значит,

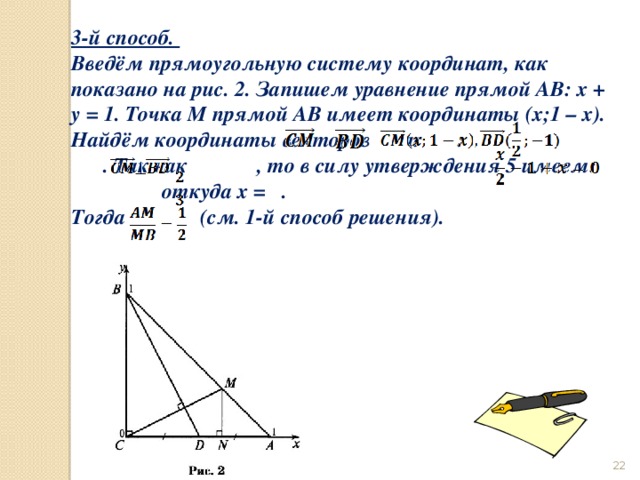
3-й способ.

Введём прямоугольную систему координат, как показано на рис. 2. Запишем уравнение прямой AB: x + y = 1. Точка M прямой AB имеет координаты (х;1 – х). Найдём координаты векторов и : . Так как , то в силу утверждения 5 имеем: откуда х = .

Тогда (см. 1-й способ решения).

4-й способ .

Обозначим точку пересечения отрезков BD и M буквой О. Введём систему координат, как показано на рис. 4. Пусть ОМ = а, ОС = b, OB = d, тогда М(а; 0), С(-b; 0), A(b; -2с), D(0; -с), В(0; d).

Исходя из того, что , , ВС = СА , , запишем систему уравнений:

откуда найдём, что d = 4c , . Теперь координаты точек можно выразить через параметры а и с: В(0; 4С), М(а; 0), А( ;-2c ) . Найдём длины отрезков МВ и МА:

.

Тогда

5-й способ. 

Пусть Тогда

(см. рис.3).

В силу утверждения 2, , тогда   . Кроме того,

Поскольку , то    или

, откуда, учитывая,

что   и , получаем       .

Тогда      

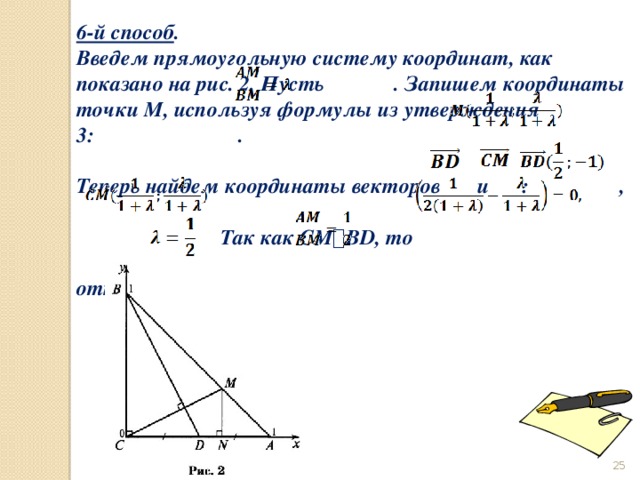
6-й способ .

Введем прямоугольную систему координат, как показано на рис. 2. Пусть . Запишем координаты точки М, используя формулы из утверждения 3:                           .

Теперь найдем координаты векторов и  : ,

Так как СМ ⟘ ВD, то

откуда         . Значит,           

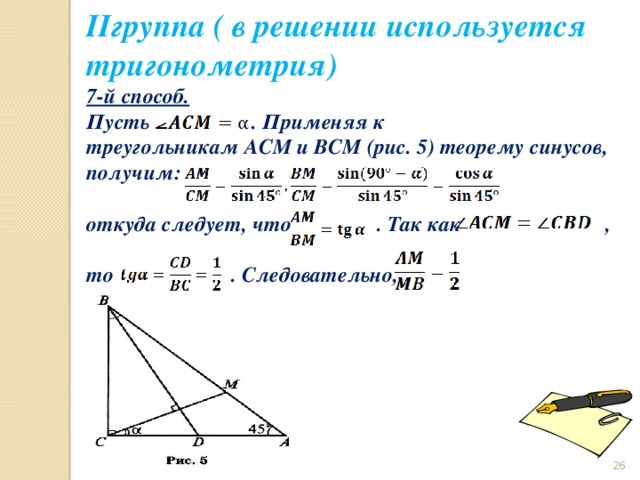
IIгруппа ( в решении используется тригонометрия)

7-й способ.  

Пусть   . Применяя к треугольникам ACM и BCM (рис. 5) теорему синусов, получим:

откуда следует, что                . Так как    ,

то                    . Следовательно,

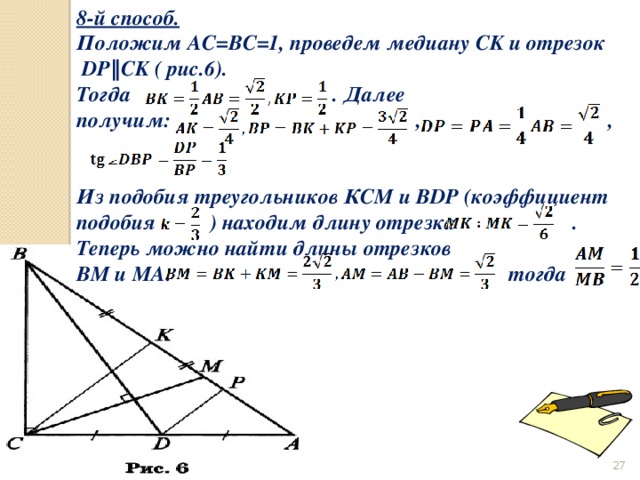
8-й способ.

Положим AC=BC=1, проведем медиану СK и отрезок  DP‖CK ( рис.6).

Тогда         . Далее

получим:                       , ,

Из подобия треугольников КСМ и BDP (коэффициент подобия  ) находим длину отрезка           . Теперь можно найти длины отрезков

ВМ и МА:           тогда

9-й способ.

Введем обозначения:   . Далее имеем:

, откуда

Применяя к треугольнику ABD теорему косинусов, находим           , тогда              .

Наконец,                                , .

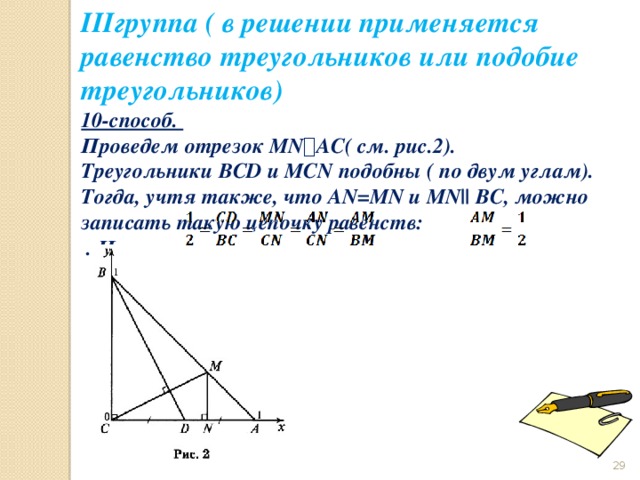
IIIгруппа ( в решении применяется равенство треугольников или подобие треугольников)

10-способ.

Проведем отрезок MN ⟘ AC( см. рис.2). Треугольники BCD и MCN подобны ( по двум углам). Тогда, учтя также, что AN=MN и MN|| BC, можно записать такую цепочку равенств:                        . Итак,              

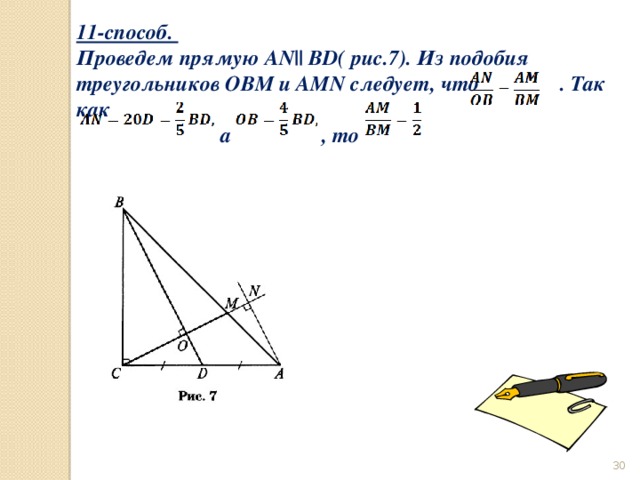
11-способ.

Проведем прямую AN|| BD( рис.7). Из подобия треугольников OBM и AMN следует, что            . Так как

а , то

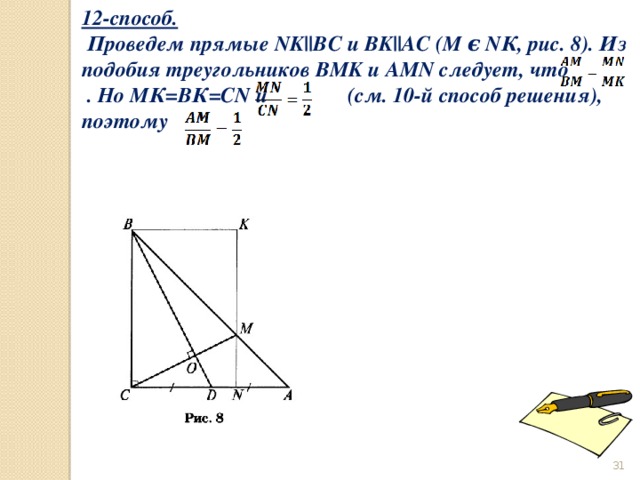
12-способ.

Проведем прямые NK||BC и BK||AC (M ϵ NК, рис. 8). Из подобия треугольников BMK и AMN следует, что           . Но МК=ВК=СN и           (см. 10-й способ решения), поэтому               

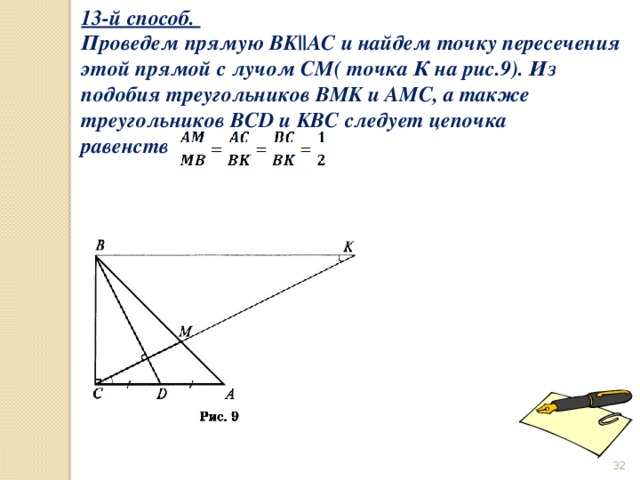
13-й способ.

Проведем прямую BK||AC и найдем точку пересечения этой прямой с лучом СМ( точка К на рис.9). Из подобия треугольников BMK и AMC, а также треугольников BCD и KBC следует цепочка равенств                              

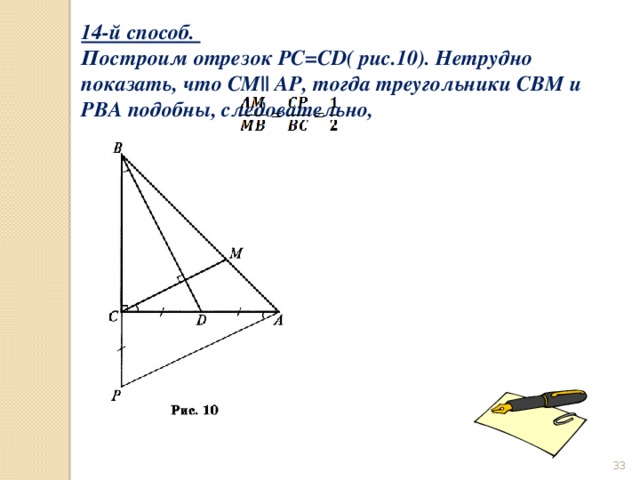
14-й способ.

Построим отрезок PC=CD( рис.10). Нетрудно показать, что CM|| AP, тогда треугольники CBM и PBA подобны, следовательно,     

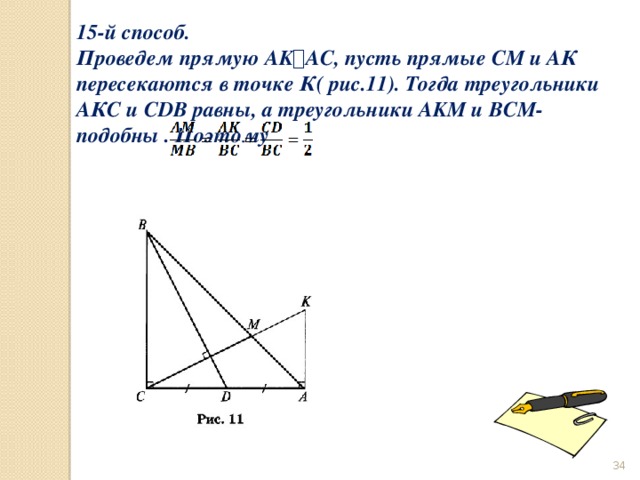
15-й способ.

Проведем прямую AK ⟘ AC, пусть прямые СМ и АК пересекаются в точке К( рис.11). Тогда треугольники АКС и CDB равны, а треугольники AKM и BCM- подобны . Поэтому                                   

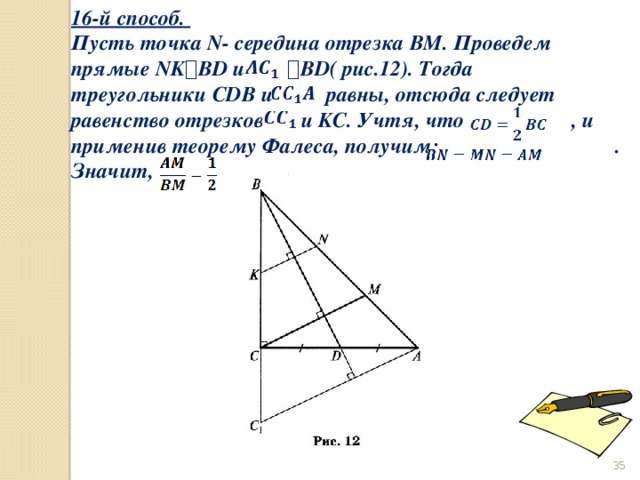
16-й способ.

Пусть точка N- середина отрезка BM. Проведем прямые NK ⟘ BD и  ⟘ BD( рис.12). Тогда треугольники CDB и    равны, отсюда следует равенство отрезков  и KC. Учтя, что                    , и применив теорему Фалеса, получим:                                 .

Значит,                         .

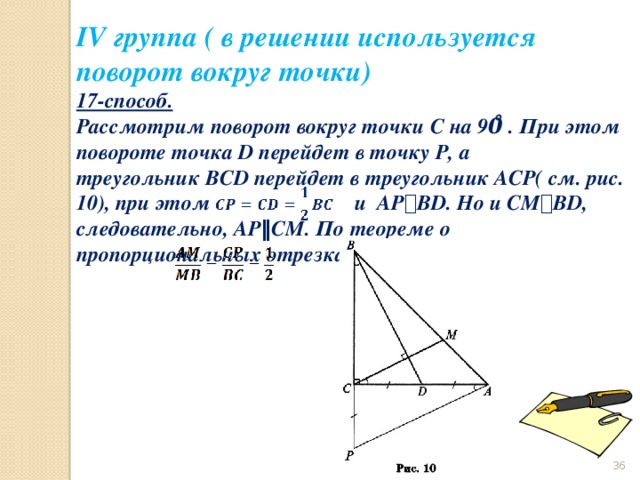
IV группа ( в решении используется поворот вокруг точки)

17-способ.

Рассмотрим поворот вокруг точки С на 90̊ . При этом повороте точка D перейдет в точку P, а треугольник BCD перейдет в треугольник ACP( см. рис. 10), при этом                           и  AP ⟘ BD. Но и CM ⟘ BD, следовательно, AP ‖ CM. По теореме о пропорциональных отрезках                      

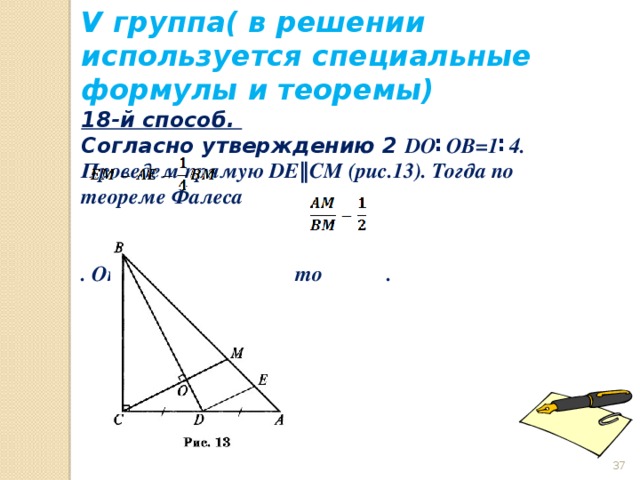
V группа( в решении используется специальные формулы и теоремы)

18-й способ.

Согласно утверждению 2 DO ∶OB=1∶4. Проведем прямую DE‖CM (рис.13). Тогда по теореме Фалеса

. Отсюда получаем, что .

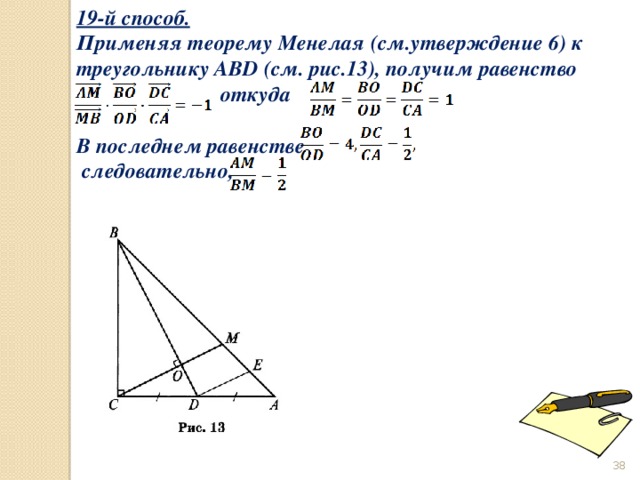
19-й способ.

Применяя теорему Менелая (см.утверждение 6) к треугольнику ABD (см. рис.13), получим равенство

откуда

В последнем равенстве

следовательно,

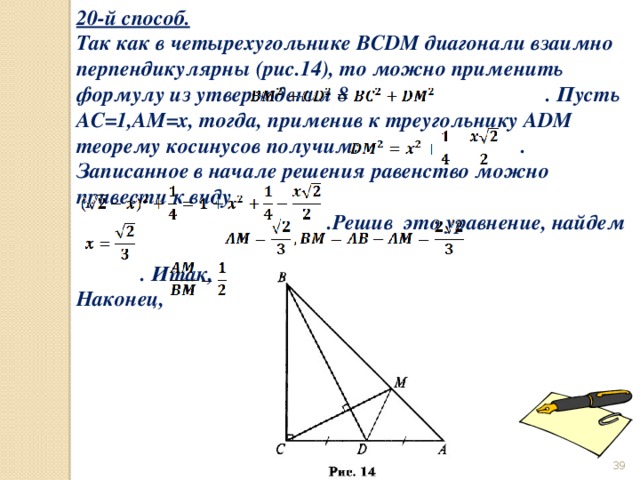
20-й способ.

Так как в четырехугольнике BCDM диагонали взаимно перпендикулярны (рис.14), то можно применить формулу из утверждения 8 . Пусть AC=1,AM=x, тогда, применив к треугольнику ADM теорему косинусов получим: . Записанное в начале решения равенство можно привести к виду

.Решив это уравнение, найдем

. Итак,

Наконец,

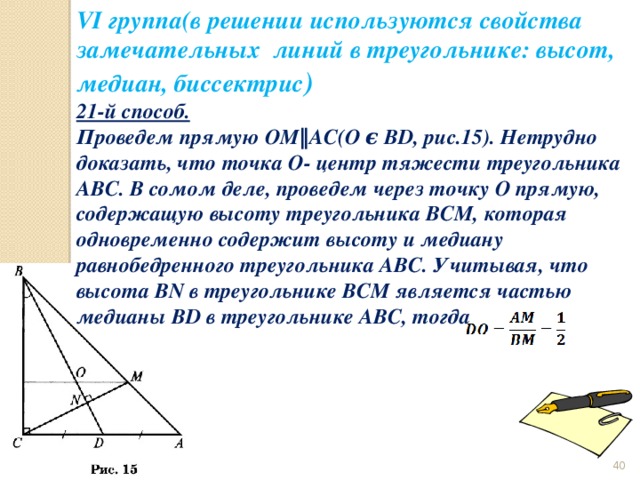
VI группа(в решении используются свойства замечательных линий в треугольнике: высот, медиан, биссектрис )

21-й способ.

Проведем прямую OM‖AC(O ϵ BD, рис.15). Нетрудно доказать, что точка O- центр тяжести треугольника ABC. В сомом деле, проведем через точку O прямую, содержащую высоту треугольника BCM, которая одновременно содержит высоту и медиану равнобедренного треугольника ABC. Учитывая, что высота BN в треугольнике BCM является частью медианы BD в треугольнике ABC, тогда

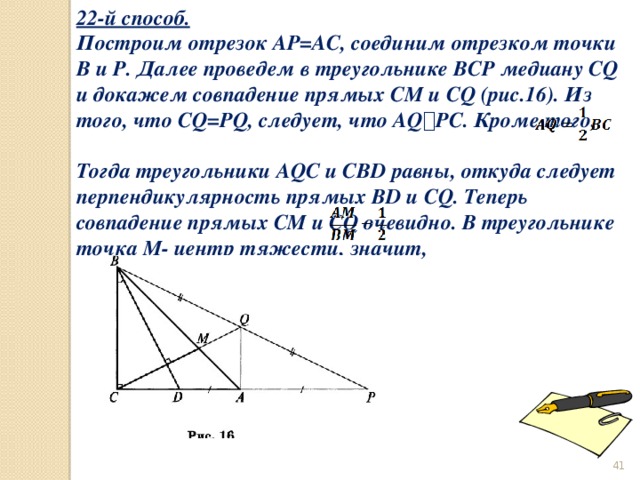
22-й способ.

Построим отрезок AP=AC, соединим отрезком точки B и P. Далее проведем в треугольнике BCP медиану CQ и докажем совпадение прямых CM и CQ (рис.16). Из того, что CQ=PQ, следует, что AQ ⟘ PC. Кроме того,

Тогда треугольники AQC и CBD равны, откуда следует перпендикулярность прямых BD и CQ. Теперь совпадение прямых CM и CQ очевидно. В треугольнике точка M- центр тяжести, значит,

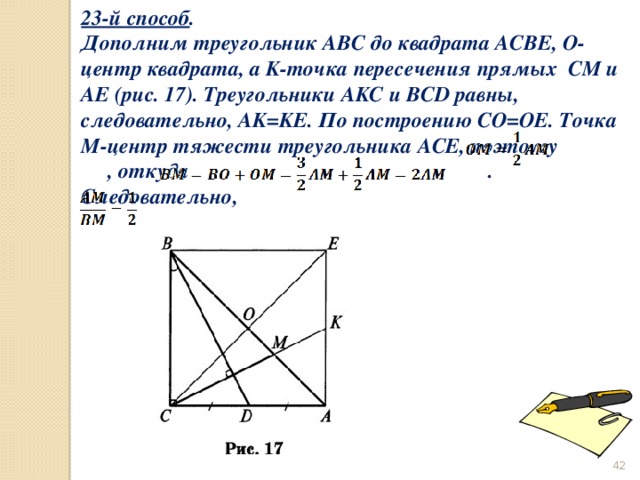
23-й способ .

Дополним треугольник ABC до квадрата ACBE, O- центр квадрата, а K-точка пересечения прямых CM и AE (рис. 17). Треугольники AKC и BCD равны, следовательно, AK=KE. По построению CO=OE. Точка M-центр тяжести треугольника ACE, поэтому , откуда . Следовательно,

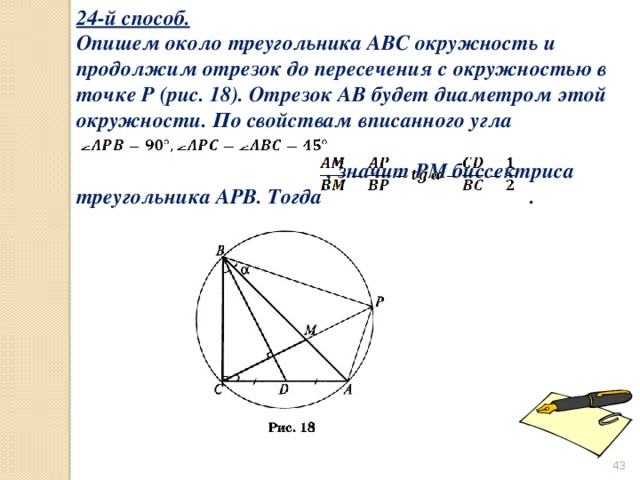
24-й способ.

Опишем около треугольника ABC окружность и продолжим отрезок до пересечения с окружностью в точке Р (рис. 18). Отрезок АВ будет диаметром этой окружности. По свойствам вписанного угла

, значит РМ биссектриса треугольника АРВ. Тогда .

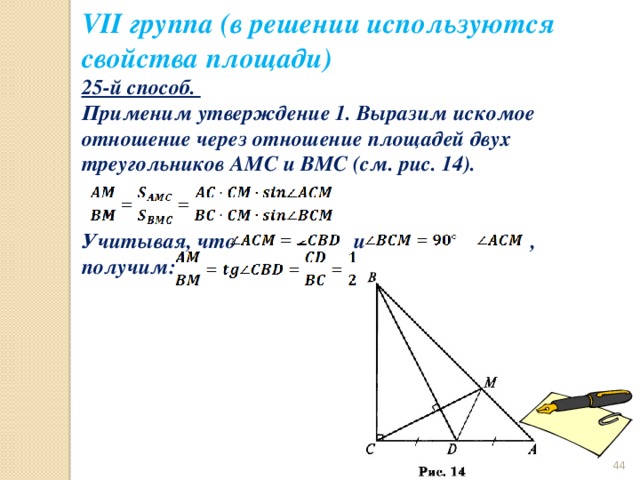
VII группа (в решении используются свойства площади)

25-й способ.

Применим утверждение 1. Выразим искомое отношение через отношение площадей двух треугольников АМС и ВМС (см. рис. 14).

Учитывая, что и , получим:

«Дорога та, что сам искал, вовек не позабудется!»