Практическая работа
«Быстрый» перевод чисел в компьютерных системах счисления
Цель: ознакомиться с правилами быстрого перевода чисел из одной системы счисления в другую.
Теоретические сведения
Из курса информатики основной школы вы знаете, что в компьютерных науках широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления, благодаря чему их называют «компьютерными». Между основаниями этих систем существует очевидная связь: 16 = 24, 8 = 23.
Способ «быстрого» перевода основан на том, что каждой цифре числа в системе счисления, основание которой q кратно степени двойки, соответствует число, состоящее из n (q = 2n) цифр в двоичной системе счисления. Замена восьмеричных цифр двоичными тройками (триадами) и шестнадцатеричных цифр двоичными четвёрками (тетрадами) позволяет осуществлять быстрый перевод между этими системами счисления, не прибегая к арифметическим операциям.
| Восьмеричная цифра | Двоичная триада |
|
| Шестнадцатеричная цифра | Двоичная тетрада |
| 0 | 000 |
|
| 0 | 0000 |
| 1 | 001 |
|
| 1 | 0001 |
| 2 | 010 |
|
| 2 | 0010 |
| 3 | 011 |
|
| 3 | 0011 |
| 4 | 100 |
|
| 4 | 0100 |
| 5 | 101 |
|
| 5 | 0101 |
| 6 | 110 |
|
| 6 | 0110 |
| 7 | 111 |
|
| 7 | 0111 |
|
|
|
|
| 8 | 1000 |
|
|
|
|
| 9 | 1010 |
|
|
|
|
| A | 1011 |
|
|
|
|
| B | 1100 |
|
|
|
|
| C | 1101 |
|
|
|
|
| D | 1101 |
|
|
|
|
| E | 1110 |
|
|
|
|
| F | 1111 |
Для того чтобы целое двоичное число записать в системе счисления с основанием q = 2n, достаточно:
1) данное двоичное число разбить справа налево на группы по n цифр в каждой;
2) если в последней левой группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой системы счисления с основанием q = =2n.
Пример 1. Переведем число 110101001112 в восьмеричную систему счисления.
110101001112 − исходное число;
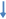
11.010.100.111 − выделяем триады;
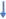
011.010.100.111 − дополняем левую группу слева нулём;
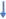
3. 2. 4. 7 − выписываем восьмеричные цифры;
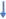
32478 − результат.
Пример 2. Переведем число 16AC16 в двоичную систему счисления.
16AC16 − исходное число;
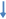
0001.0110.1010.1100 − заменяем каждую цифру тетрадой;
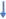
1.0110.1010.1100 − убираем слева незначащие нули;
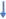
10110101011002 − результат.
Через двоичную систему счисления можно проводить быстрые переводы из восьмеричной системы счисления в шестнадцатеричную и обратно (рис. 1)


Восьмеричные (шестнадцатеричные) цифры заменяются триадами (тетрадами)
A2

Двоичные триады (тетрады) заменяем на шестнадцатеричные (восьмеричные) цифры




A8(16)
A16(8)
Рис. 1. Схема перевода целых чисел из восьмеричной системы счисления в шестнадцатеричную и обратно через двоичную систему счисления
Пример 3. Выполним перевод восьмеричного 672528 числа в шестнадцатеричную систему счисления.
672528 − исходное число;
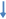
110.111.010.101.010 − заменяем каждую цифру триадой;
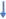
110.1110.1010.1010 − дополняем левую группу слева нулём;
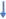
6 . E . A. A − выписываем шестнадцатеричные цифры;
6EAA16 − результат.
Аналогичные алгоритмы быстрого перевода существуют и для дробных чисел. Для того чтобы записать правильную двоичную дробь в системе счисления с основанием q = 2n, достаточно:
1) двоичное число разбить слева направо на группы по n цифр в каждой;
2) если в последней правой группе окажется меньше n разрядов, то её надо дополнить справа нулями до нужного числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой системы счисления с основанием q = 2n.
Пример 4. Число 0,1011000112 заменим равным ему шестнадцатеричным числом.
0,1011000112 − исходное число;
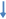
0,1011.0001.1 − разбиваем двоичную строку слева направо на тетрады;
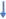
0,1011.0001.1000 − дополняем правую группу справа нулями;
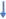
0, B . 1 . 8 − выписываем шестнадцатеричные цифры;
0,B1816 − результат.
Содержание работы
Задание 1. Переведите двоичные числа в восьмеричную систему счисления:
1) 1010001001011;
2) 1010,00100101.
Задание 2. Переведите двоичные числа в шестнадцатеричную систему счисления:
1) 1010001001011;
2) 1010,00100101.
Задание 3. Переведите числа в двоичную систему счисления:
1) 2668;
2) 26616.
Задание 4. Переведите числа из восьмеричной системы счисления в шестнадцатеричную:
1) 12754;
2) 1515.
Задание 5. Переведите числа из шестнадцатеричной системы счисления в восьмеричную:
1) 1АЕ2;
2) 1С1С.
Задание 6. Сравните числа:
1) 12516 и 1111000101012;
2) 7578 и 11100101012;
3) А2316 и 12328.
Задание 7. Сделайте вывод о проделанной работе.
6