Четыре замечательные точки треугольника

Четыре замечательные точки треугольника

К учебнику Л.С.Атанасяна Геометрия 7 - 9, Глава VIII, п. 74-76, 8 класс

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

∟

∟

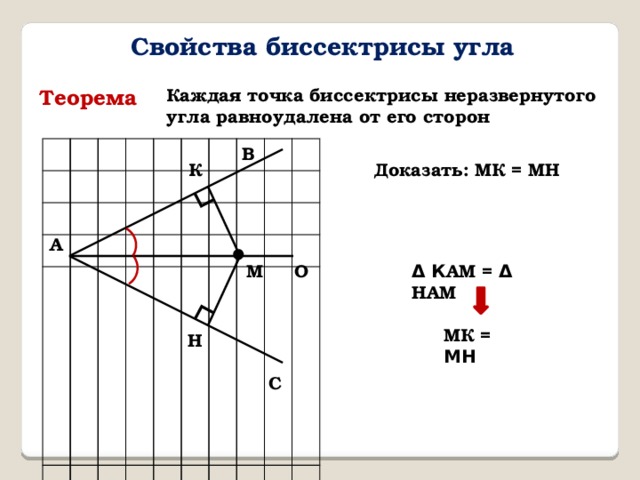
Свойства биссектрисы угла

Теорема

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон

В

Доказать: МК = МН

К

А

О

М

Δ К АМ = Δ НАМ

МК = МН

Н

С

∟

∟

ǁ

ǁ

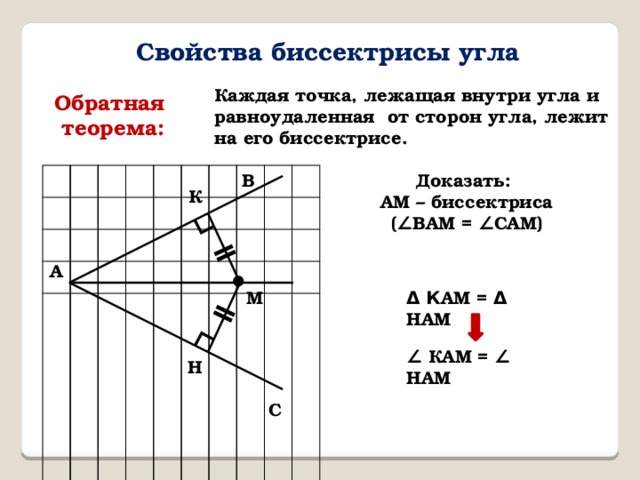
Свойства биссектрисы угла

Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.

Обратная

теорема:

Доказать:

В

АМ – биссектриса

( ∠ ВАМ = ∠ САМ)

К

А

М

Δ К АМ = Δ НАМ

∠ КАМ = ∠ НАМ

Н

С

∟

ǁ

ǁ

∟

ǁ

ǁ

ǁ

ǁ

∟

∟

∟

∟

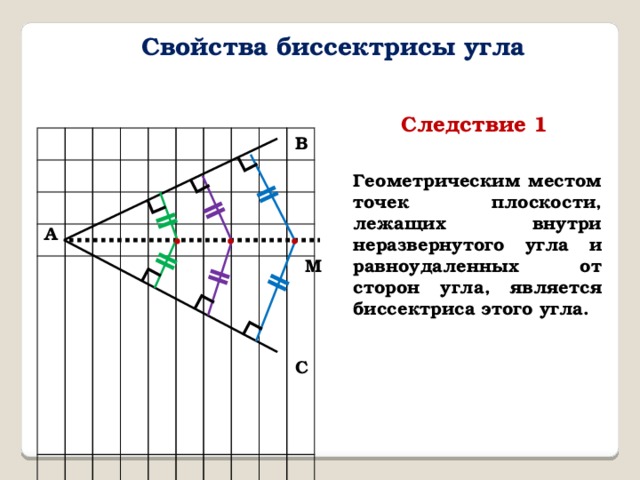
Свойства биссектрисы угла

Следствие 1

В

Геометрическим местом точек плоскости, лежащих внутри неразвернутого угла и равноудаленных от сторон угла, является биссектриса этого угла.

А

М

С

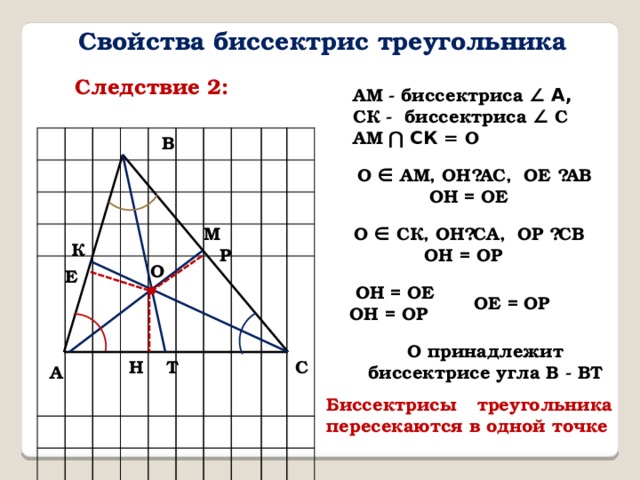
Свойства биссектрис треугольника

Следствие 2:

АМ - биссектриса ∠ А,

СК - биссектриса ∠ С

АМ ⋂ СК = О

В

О ∈ АМ, ОН⏊АС, ОЕ ⏊АВ

ОН = ОЕ

О ∈ СК, ОН⏊СА, ОР ⏊СВ

М

ОН = ОР

К

Р

О

Е

ОН = ОЕ

ОН = ОР

ОЕ = ОР

О принадлежит биссектрисе угла В - ВТ

Н

С

Т

А

Биссектрисы треугольника пересекаются в одной точке

ǁ

ǁ

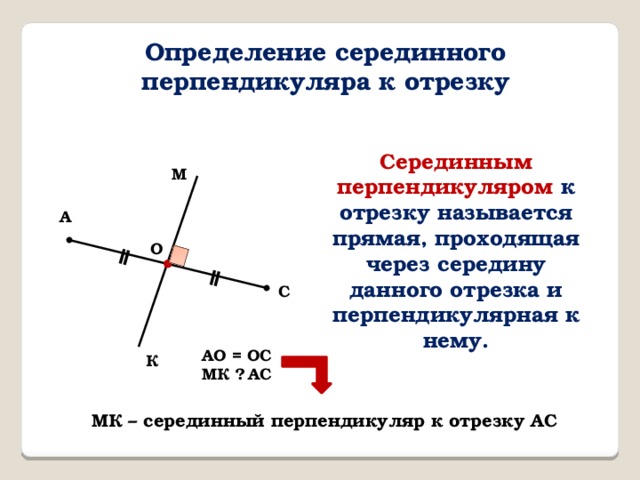
Определение серединного перпендикуляра к отрезку

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

М

А

О

С

АО = ОС

МК ⏊ АС

К

МК – серединный перпендикуляр к отрезку АС

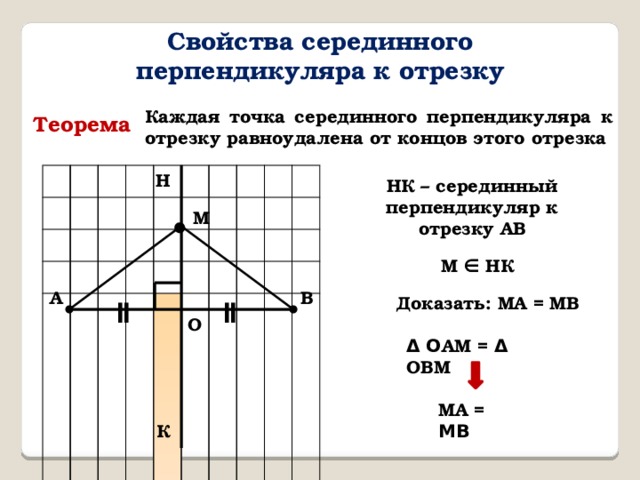
Свойства серединного перпендикуляра к отрезку

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка

Теорема

Н

НК – серединный перпендикуляр к отрезку АВ

М

М ∈ НК

А

В

Доказать: МА = МВ

ǁ

ǁ

О

Δ О АМ = Δ ОВМ

МА = МВ

К

ǁ

ǁ

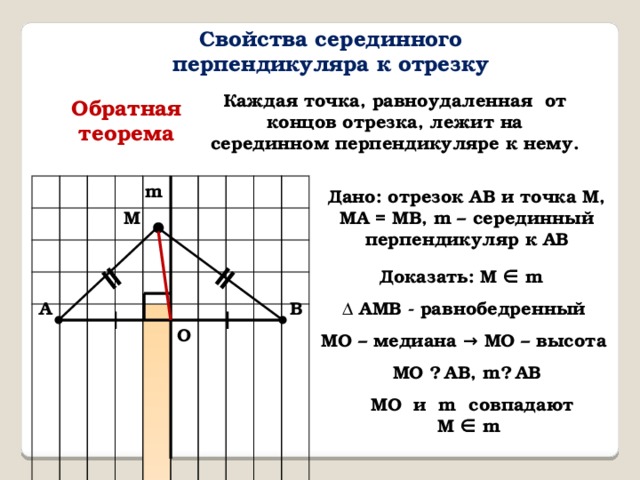
Свойства серединного перпендикуляра к отрезку

Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Обратная

теорема

m

Дано: отрезок АВ и точка М,

МА = МВ, m – серединный перпендикуляр к АВ

М

Доказать: М ∈ m

А

В

Δ АМВ - равнобедренный

∣

∣

О

МО – медиана → МО – высота

МО ⏊ АВ, m⏊ АВ

МО и m совпадают

M ∈ m

ǁ

ǁ

⫴

⫴

Ѕ

Ѕ

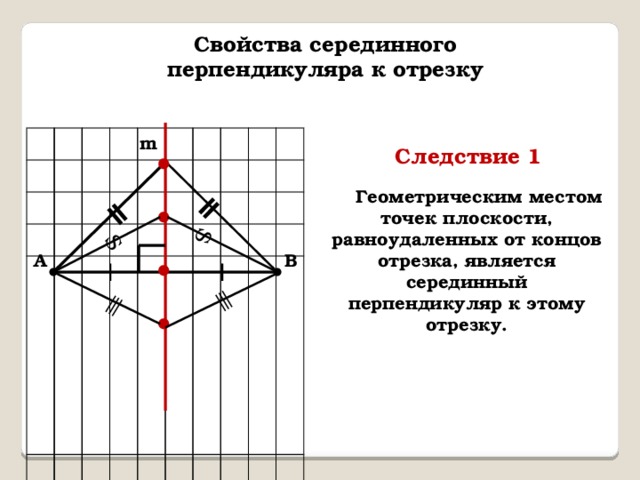
Свойства серединного перпендикуляра к отрезку

m

Следствие 1

Геометрическим местом точек плоскости, равноудаленных от концов отрезка, является серединный перпендикуляр к этому отрезку.

В

А

∣

∣

ǁ

ǁ

ǁ

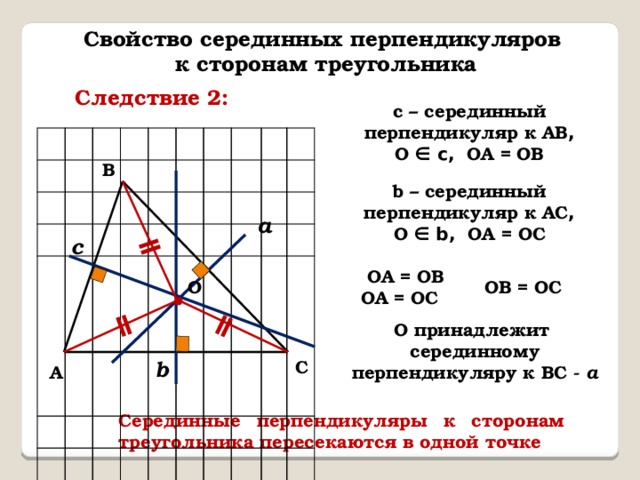
Свойство серединных перпендикуляров

к сторонам треугольника

Следствие 2:

с – серединный перпендикуляр к АВ ,

О ∈ с, ОА = ОВ

В

b – серединный перпендикуляр к АС ,

О ∈ b, ОА = ОC

а

с

OA = ОB

OA = ОC

ОB = ОC

О

О принадлежит серединному перпендикуляру к ВС - a

b

С

А

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке

∣

ǁ

ǁ

∣

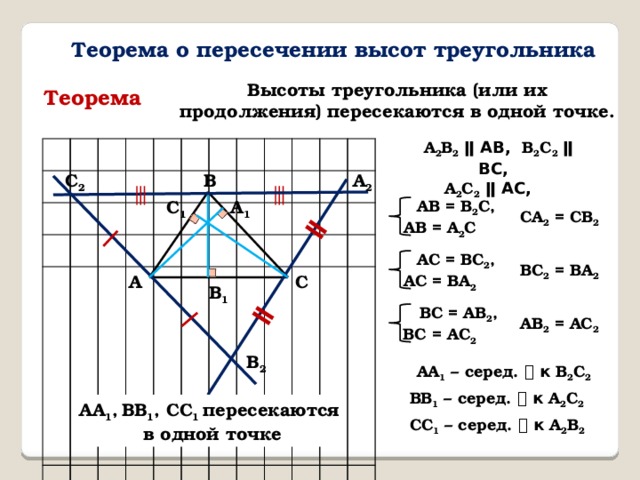
Теорема о пересечении высот треугольника

Высоты треугольника (или их продолжения) пересекаются в одной точке.

Теорема

А 2 В 2 ǁ АВ, В 2 С 2 ǁ ВС,

А 2 С 2 ǁ АС,

С 2

А 2

В

⫴

⫴

А 1

С 1

АВ = В 2 С,

АВ = А 2 С

СА 2 = СВ 2

АС = ВС 2 ,

АС = ВА 2

ВС 2 = ВА 2

С

А

В 1

ВС = АВ 2 ,

ВС = АС 2

АВ 2 = АС 2

В 2

АА 1 – серед. ⏊ к В 2 С 2

ВВ 1 – серед. ⏊ к А 2 С 2

АА 1 , ВВ 1 , СС 1 пересекаются

в одной точке

СС 1 – серед. ⏊ к А 2 В 2

∟

∟

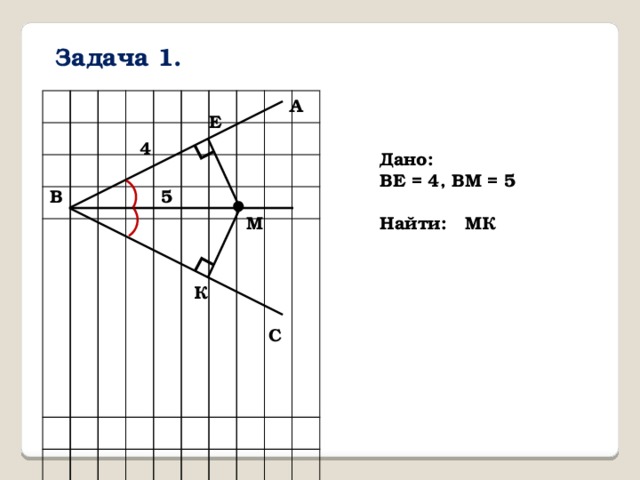
Задача 1.

А

Е

4

Дано:

ВЕ = 4, ВМ = 5

В

5

М

Найти: МК

К

С

∟

∟

ǁ

ǁ

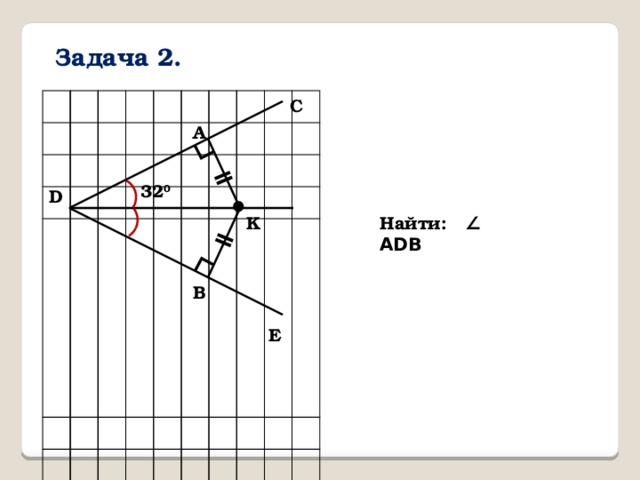
Задача 2.

C

A

32 0

D

K

Найти: ∠ ADB

B

E

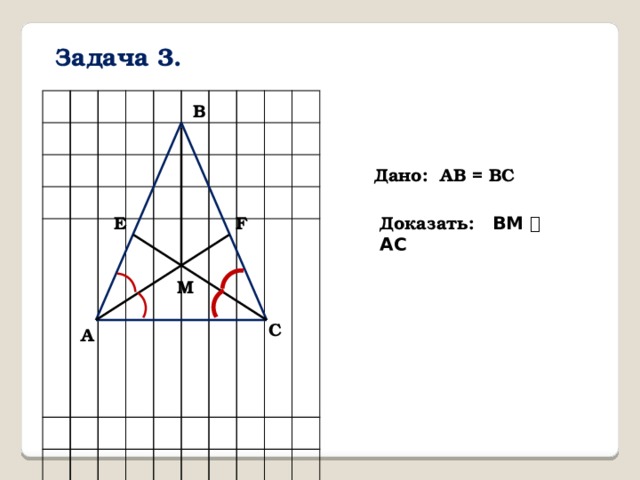
Задача 3.

B

Дано: AB = BC

Доказать: ВМ ⏊ АС

E

F

M

C

A

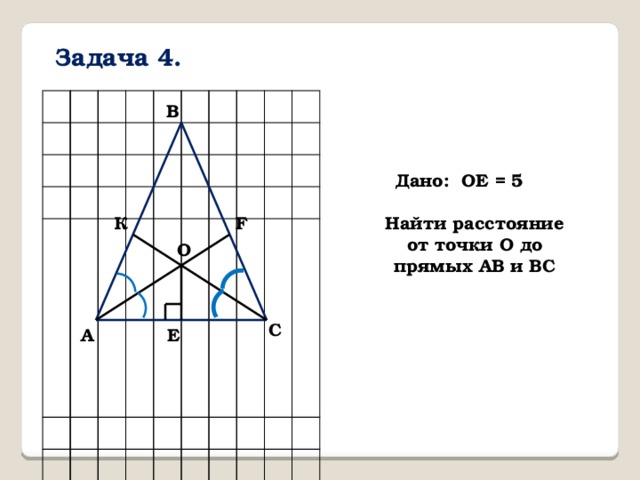
Задача 4.

B

Дано: ОЕ = 5

Найти расстояние от точки О до прямых АВ и ВС

К

F

О

C

A

Е

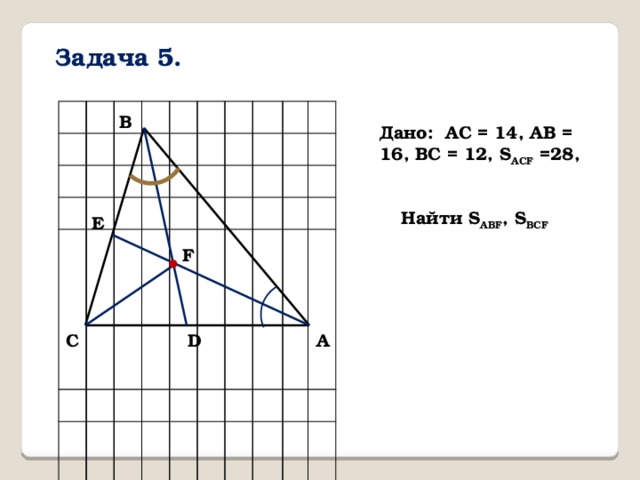
Задача 5.

В

Дано: AC = 14, AB = 16, BC = 12, S ACF =28,

Найти S ABF , S BCF

Е

F

С

А

D

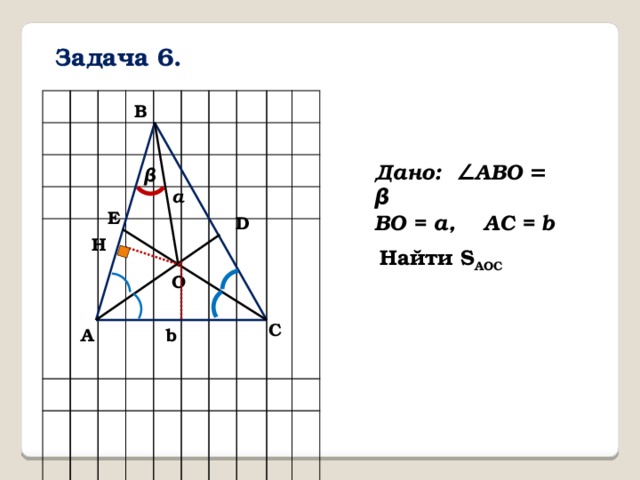
Задача 6.

B

Дано: ∠ABO = β

BO = a, AC = b

β

a

E

D

H

Найти S AOC

O

C

A

b

ǁ

ǁ

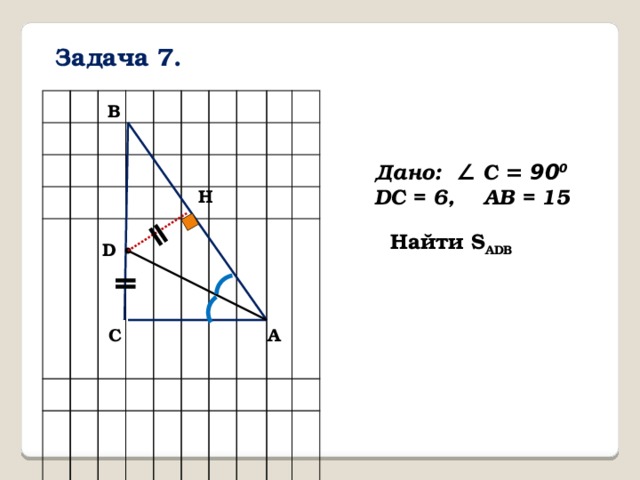
Задача 7.

B

Дано: ∠ С = 90 0

DC = 6, AB = 15

H

Найти S ADB

D

C

A

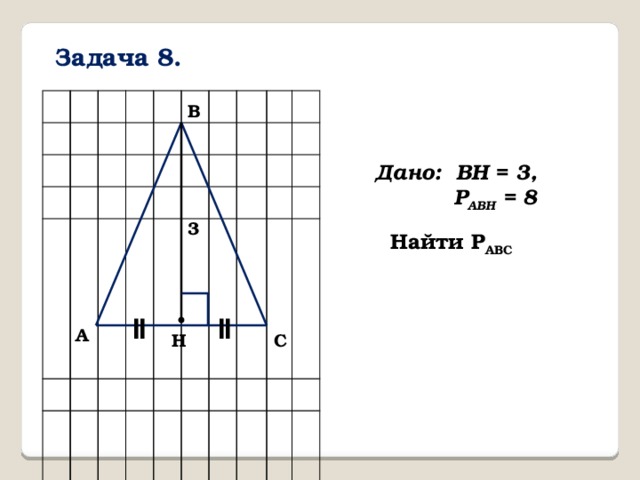
Задача 8.

B

Дано: BH = 3,

P ABH = 8

3

Найти P ABC

ǁ

ǁ

A

C

H

∣

ǁ

ǁ

∣

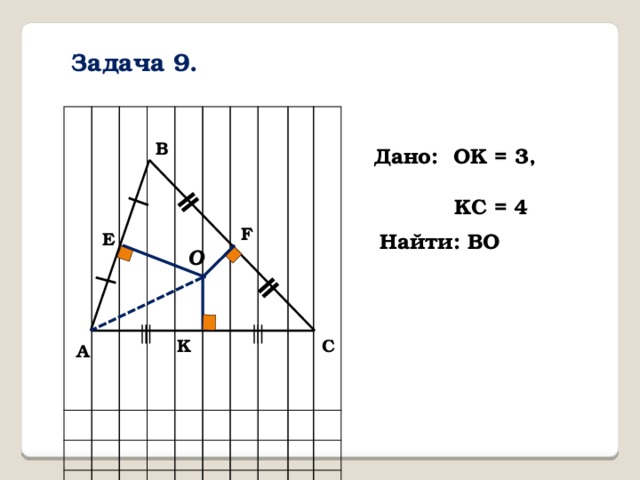
Задача 9.

В

Дано: OK = 3,

KC = 4

F

E

Найти: BO

O

⫴

⫴

С

K

А

∣

ǁ

ǁ

∣

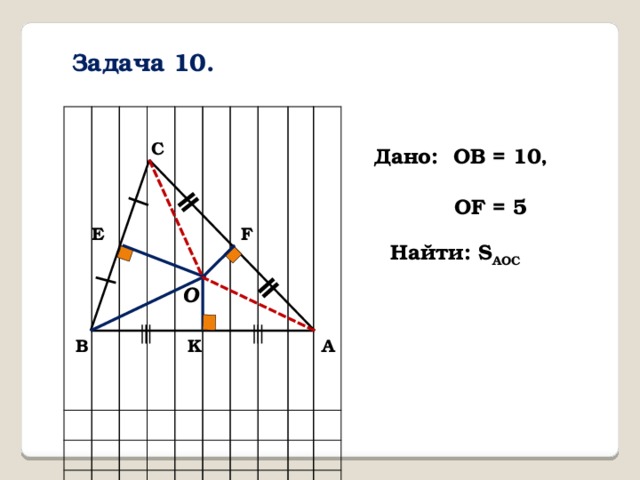
Задача 10.

С

Дано: OB = 10,

ОF = 5

E

F

Найти: S AOC

O

⫴

⫴

K

В

А

ǁ

ǁ

ǁ

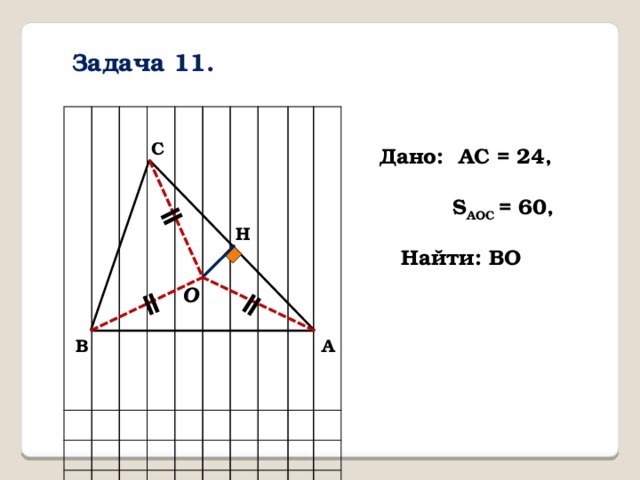
Задача 11.

С

Дано: AC = 24,

S AOC = 60,

H

Найти: BO

O

В

А

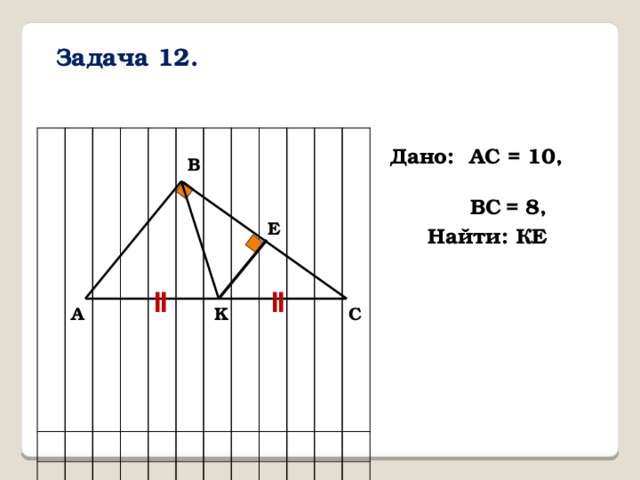
Задача 12.

Дано: AC = 10,

ВС = 8,

В

E

Найти: КЕ

ǁ

ǁ

K

С

А

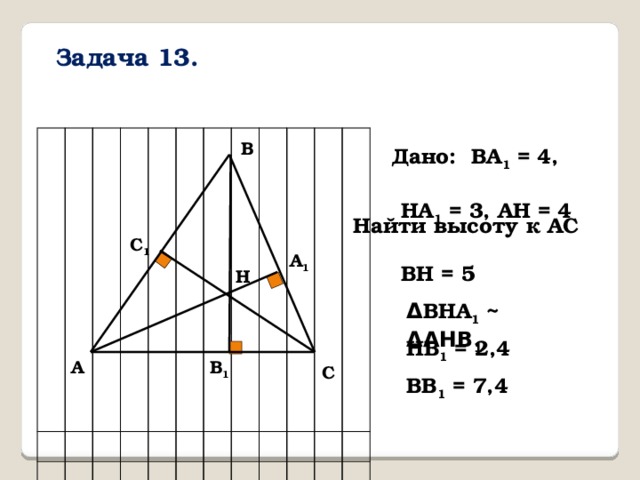
Задача 13.

В

Дано: ВA 1 = 4,

НA 1 = 3, АН = 4

Найти высоту к АС

С 1

А 1

ВН = 5

Н

Δ ВНА 1 ~ ΔАНВ 1

НВ 1 = 2,4

В 1

А

С

ВВ 1 = 7,4

∣

ǁ

ǁ

∣

3

4

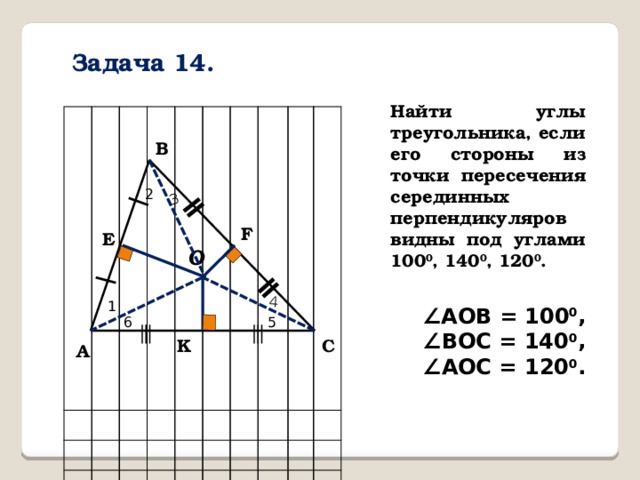
Задача 14.

Найти углы треугольника, если его стороны из точки пересечения серединных перпендикуляров видны под углами 100 0 , 140 0 , 120 0 .

В

2

F

E

O

1

∠ АОВ = 100 0 ,

∠ ВОС = 140 0 ,

∠ АОС = 120 0 .

5

6

⫴

⫴

С

K

А

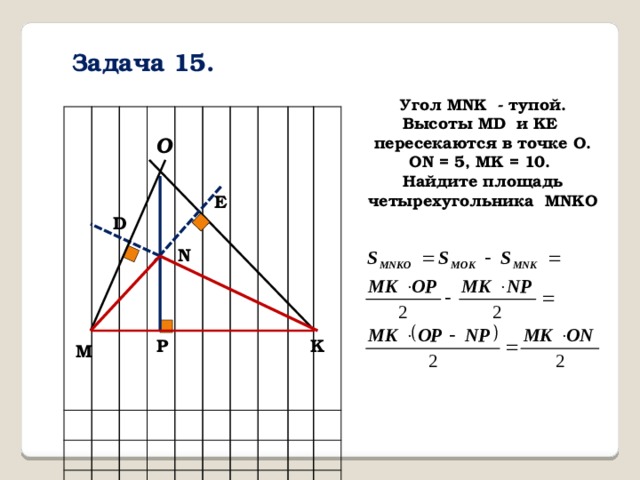
Задача 15.

Угол MNK - тупой. Высоты MD и KE пересекаются в точке О. ON = 5, MK = 10.

Найдите площадь четырехугольника MNKO

O

E

D

N

K

P

M