8 класс Алгебра 8.12.20 Функции.

8/12/20 Алгебра 8 класс
Тема урока Функция . Свойства и график.Использование графиков функций для решения уравнений и систем.Модуль действительного числа.График функции у=|х|. Тождество «корень из а²=|а|»

Ссылка на видеоурок https://youtu.be/cNZmGi1rONQ

Запиши число и Классная работа.
Ниже запиши тему урока

На данном уроке мы познакомимся с функцией, ее свойствами и графиком. Изучение свойств функции поможет нам с решением различных задач, связанных с квадратным корнем. Кроме того, мы познакомимся с понятием выпуклости функции (выпуклости вверх и выпуклости вниз).

Вспомни.

Квадратным корнем из неотрицательного числа   называют такое неотрицательное число, квадрат которого равен  . Это число обозначают  , число   называют подкоренным числом.

Примеры:

1.   ( ,  )

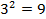2.   ( ,  )

Обратите внимание:

 , но   – корень не может быть равен отрицательному числу.

 – нельзя вычислить. Корня квадратного из отрицательного числа не существует.

Функцией  , где  , называется закон, который каждому неотрицательному числу   сопоставляет число  .

Функция   нам уже известна. Это функция типа  . Таким образом, изучать функцию   мы будем на базе функции  , где  .

Графиком функции   является ветвь параболы. Проверим это, составив таблицу.

Построим найденные точки на координатной плоскости (см. Рис. 1).

Рис. 1. График функции 

Прочтем график:

Если аргумент возрастает от 0 до  , функция возрастает от 0 до  .

1. Множество значений функции   – это луч  .

Докажем это свойство

Доказательство

Пусть   – это произвольное число из промежутка  . Найдется ли такое  , при котором  ? Чтобы узнать это, решим уравнение:

Число   достигается, когда аргумент равен   (см. Рис. 2).

Рис. 2. Иллюстрация к доказательству

Следовательно:

Что и требовалось доказать.

Следствия из данного свойства

а) Функция   не ограничена сверху. То есть на оси   для этой функции нет самого большого положительного числа.

б) Функция ограничена снизу и имеет наименьшее значение.

в)   при всех  .

2. Функция   монотонно возрастает на всей области определения, то есть при  .

 Примечание:

Функция называется монотонно возрастающей на всей области определения, если для любых   и  , принадлежащих области определения, из неравенства   следует неравенство  .

Рисунок 3 иллюстрирует нам, что функция   является монотонно возрастающей.

Рис. 3. Функция   монотонно возрастающая

3. Функция   выпукла вверх на всей области определения.

Для любых двух точек, например   и   (см. Рис. 4), дуга, лежащая между этими точками, будет находиться над отрезком, соединяющим эти две точки, следовательно, функция выпуклая вверх.

Рис. 4. Функция   выпуклая вверх

Теперь отдохните 15 минут и продолжайте урок.

Модуль действительного числа

ссылка на видеоурок https://youtu.be/oYa_Am-NKiw

Функция y = |x|.