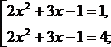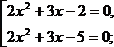831, 20.03.2020 Практическая работа: "Основные приемы решения рациональных уравнений".

Многие уравнения с помощью различных приемов, выполнив подходящие замены переменных, можно свести к квадратным. Рассмотрим некоторые из них.

1) 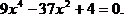  Такое уравнение называется биквадратным.

Замена: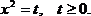 
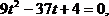 D = 1225 =  ,     

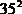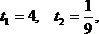
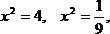
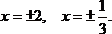
Ответ: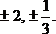 

2) 

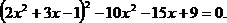
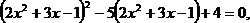
Замена: 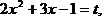  тогда получим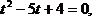   

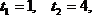
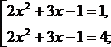
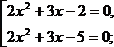
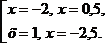
Ответ: –2,5, –2, 0,5, 1.

3) В уравнении 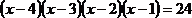 , перемножая попарно скобки, получим  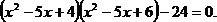 Сделав замену  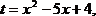 сводим уравнение к квадратному.

4)   О.Д.З.: 

Замена:   тогда     получаем   
 т.к. х 0, то получаем   

Ответ: –1, –2, 

5) Симметрическим уравнением называется уравнение вида   где  Заметим, что симметрическое уравнение нечетной степени имеет корень х = –1, симметрическое уравнение четной степени можно решить, используя замену   В школьном курсе математики часто встречаются симметрические уравнения четвертой степени, которые в общем виде можно записать так:   где
Решим уравнение   О.Д.З.:  R.
Заметим, что х = 0 не является корнем уравнения, поэтому, разделив обе части уравнения на  , получим уравнение   
Пришли к уравнению, решение которого рассмотрено в п.4.

6) Возвратным уравнением нечетной степени называется уравнение вида   где  R.

Возвратное уравнение четной степени – это уравнение вида   где  R.

Заметим, что возвратное уравнение нечетной степени имеет корень 

Решим возвратное уравнение четверной степени 
О.Д.З.:  R. Заметим, что   Разделив обе части уравнения на  ( , получим   
Замена :   тогда 
   

Ответ: 

7) Однородным уравнением  ой степени называется уравнение вида   которое заменой   сводится к алгебраическому уравнению  ой степени.

Решим уравнение, которое сводится к однородному уравнению четвертой степени:

 О.Д.З.: R.
 Заметим, что  , поэтому можем разделить обе части уравнения на выражение  , получим
, это уравнение заменой   сводится к квадратному уравнению 

Рассмотрим еще некоторые уравнения, сводящиеся к квадратным.

8)  О.Д.З.:  R.
Заметим, что х = 0 не является корнем уравнения, поэтому можем разделить обе части его на   получим   

Замена:   Получаем квадратное уравнение   

При решении последних уравнений мы пользовались утверждением: при умножении или делении обеих частей уравнения на число или выражение, не равное нулю на области допустимых значений переменной, получаем уравнение, равносильное данному.

Можно использовать и другое утверждение: при делении числителя и знаменателя дроби на число или выражение, не равное нулю на области допустимых значений переменной, получаем уравнение, равносильное данному. Покажем, как используется это утверждение.

9)   О.Д.З.:  R 

Заметим, что х = 0 не является корнем уравнения, поэтому, разделив числитель и знаменатель каждой дроби на х, получим   Замена:   тогда   

10) При решении уравнения вида   можно воспользоваться заменой

Решим уравнение:   Сделаем замену:     получим         

Ответ: –5, 1.

11) Рассмотрим метод выделения полного квадрата при решении рационального уравнения.

 О.Д.З.:
 
 

Выполнив замену   получим квадратное уравнение 

12) Покажем, как при решении уравнений может значительно упростить решение выделение целой части дробного выражения.

 О.Д.З.: 

Выделять целую часть можно делением «уголком» числителя на знаменатель или, например, следующим образом:   Выполняя аналогичные преобразования каждой дроби, получим 
   замена: 

Ответ: 

13) Уравнения вида  иногда можно решить, раскладывая левую часть уравнения на множители. Раскладывать на множители можно разными способами (вынесением общего множителя за скобки, способом группировки и т.д.) .Рассмотрим один из способов, основанный на подборе корней уравнения по его коэффициентам.

Теорема. Пусть   – многочлен с целыми коэффициентами. Если  – его рациональный корень (  – несократимая дробь), то   делится на 
 делится на  .

Эту теорему можно применять для нахождения корней уравнения с целыми коэффициентами. Если коэффициенты в уравнении не являются целыми числами, то предварительно необходимо умножить обе части его на наименьший общий знаменатель и получить уравнение с целыми коэффициентами.

Решим уравнение: 

Если уравнение имеет рациональные корни, то все они содержатся среди возможных значений дроби   Проверить, являются ли числа  корнями данного уравнения можно по следующему правилу: если х = 1 является корнем уравнения, то сумма всех его коэффициентов равна 0, если х = –1 является корнем уравнения, то сумма коэффициентов, стоящих на четных местах равна сумме коэффициентов, стоящих на нечетных местах. Нетрудно увидеть, что один из корней нашего уравнения равен 1, а, следовательно, в разложении левой части уравнения на множители будет присутствовать множитель 

Второй множитель можно найти либо, разделив многочлен   на   «уголком», либо, применяя схему Горнера.

Получаем,   Можно и дальше применять схему Горнера, а можно, получив квадратный трехчлен, находить его корни по известным формулам.
В итоге получим 

Ответ: –3; –2; 0,5; 1.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:
1)
2) 
3) 
4)