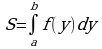Интеграл. Формула Ньютона-Лейбница.
Определенным интегралом 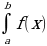 в пределах от а до в от функции f(x), непрерывной на отрезке [а, в], называется приращение любой ее первообразной F(x) при изменении аргумента х от значения х=а до х=в:
в пределах от а до в от функции f(x), непрерывной на отрезке [а, в], называется приращение любой ее первообразной F(x) при изменении аргумента х от значения х=а до х=в:
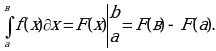
Данная формула так же называется формулой Ньютона-Лейбница, ее называют основной формулой интегрального исчисления.
Свойства определенного интеграла.
Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых функций: 
Постоянный множитель можно выносить за знак определенного интеграла: 
При перестановке пределов интегрирования определенный интеграл меняет свой знак на противоположный: 
Определенный интеграл с одинаковыми пределами равен нулю: 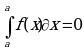
Отрезок интегрирования можно разбивать на части: 
ПРИМЕРЫ: Вычислить интеграл:
1)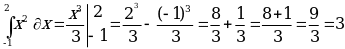 ;
;
2) 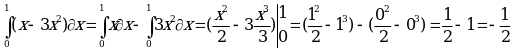 ;
;
3) 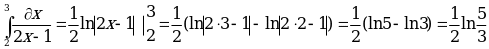 ;
;
4)  ;
;
Применение определенного интеграла
к вычислению площадей плоских фигур
Как известно, определенный интеграл от непрерывной неотрицательной функции равен площади соответствующей криволинейной трапеции (геометрический смысл определенного интеграла):
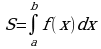 .
.
С помощью определенного интеграла можно также вычислять площади плоских фигур, так как эта задача всегда сводится к вычислению площадей криволинейных трапеций.
Площадь всякой плоской фигуры в прямоугольной системе координат может быть составлена из площадей криволинейных трапеций, прилегающих к оси 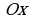 или к оси
или к оси 
Задачи на вычисление площадей плоских фигур удобно решать по следующему плану:
По условию задачи делают схематический чертеж.
Представляют искомую площадь как сумму или разность площадей криволинейных трапеций. Из условия задачи и чертежа определяют пределы интегрирования для каждой составляющей криволинейной трапеции.
Записывают каждую функцию в виде  .
.
Вычисляют площади каждой криволинейной трапеции и площадь искомой фигуры.
1) Площади фигур, расположенных над осью 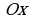
Пусть на отрезке  функция
функция  принимает неотрицательные значения, т.е.
принимает неотрицательные значения, т.е.  для любого
для любого 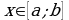 . Тогда график функции
. Тогда график функции  расположен над осью
расположен над осью 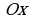 .
.
Если фигура, расположенная над осью 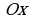 , является криволинейной трапецией, то ее площадь вычисляется по известной формуле
, является криволинейной трапецией, то ее площадь вычисляется по известной формуле
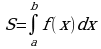 или
или  ,
,
где у находится из уравнения кривой.
2) Площади фигур, расположенных полностью или частично над осью 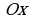
Пусть на отрезке  задана неположительная непрерывная функция
задана неположительная непрерывная функция  , т.е.
, т.е.  для любого
для любого 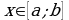 . Тогда график функции расположен под осью
. Тогда график функции расположен под осью 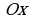 .
.
Если фигура, расположенная под осью 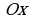 , является криволинейной трапецией , то ее площадь вычисляется по известной формуле
, является криволинейной трапецией , то ее площадь вычисляется по известной формуле
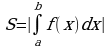 или
или 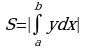 ,
,
где у находится из уравнения кривой.
Пусть функция 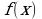 непрерывна на отрезке
непрерывна на отрезке  и принимает на этом отрезке как положительные, так и отрицательные значения. Тогда нужно разбить отрезок
и принимает на этом отрезке как положительные, так и отрицательные значения. Тогда нужно разбить отрезок  на такие части, в каждом из которых функция не изменяет знак, затем по приведенным выше формулам вычислить соответствующие этим частям площади и найденные площади сложить. Например, площадь фигуры такова:
на такие части, в каждом из которых функция не изменяет знак, затем по приведенным выше формулам вычислить соответствующие этим частям площади и найденные площади сложить. Например, площадь фигуры такова:

3) Площади фигур, прилегающих к оси 
Если криволинейная трапеция прилегает к оси ординат и ограничена непрерывной кривой  , прямыми
, прямыми 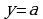 ,
, 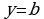 и осью
и осью  (рис.8), то ее площадь вычисляется по формуле
(рис.8), то ее площадь вычисляется по формуле
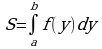
4) Симметрично расположенные плоские фигуры
Если кривая расположена симметрично относительно оси координат или начала координат, то можно упростить вычисления, определив половину площади и затем удвоив результат.







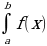 в пределах от а до в от функции f(x), непрерывной на отрезке [а, в], называется приращение любой ее первообразной F(x) при изменении аргумента х от значения х=а до х=в:
в пределах от а до в от функции f(x), непрерывной на отрезке [а, в], называется приращение любой ее первообразной F(x) при изменении аргумента х от значения х=а до х=в: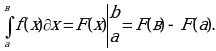



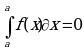

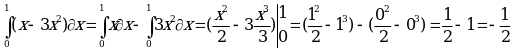 ;
; ;
;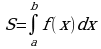 .
.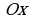 или к оси
или к оси 
 .
. функция
функция  для любого
для любого 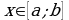 . Тогда график функции
. Тогда график функции  ,
,  для любого
для любого 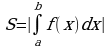 или
или 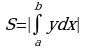 ,
, 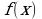 непрерывна на отрезке
непрерывна на отрезке 
 , прямыми
, прямыми 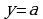 ,
, 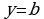 и осью
и осью