Открытый урок на квадрат и куб числа в 5 класса..

5-й класс

Открытый урок по теме:

"Квадрат и куб числа".

Задачи урока.

• Образовательная: формировать понятие степени числа (на примере квадрата и куба числа) через преобразование произведения одинаковых множителей в степень;

• Развивающая: развивать мыслительные операции (анализ, синтез, сравнение, обобщение) при преобразовании произведения одинаковых множителей в степень;

• Воспитывающая: воспитывать добросовестное отношение к учебному труду, осознанной дисциплины.

Оборуджование:  компьютер, интерактивная доска.

Дидактические материалы:

• Н.Я.Виленкин “Математика 5 класс” (учебник)

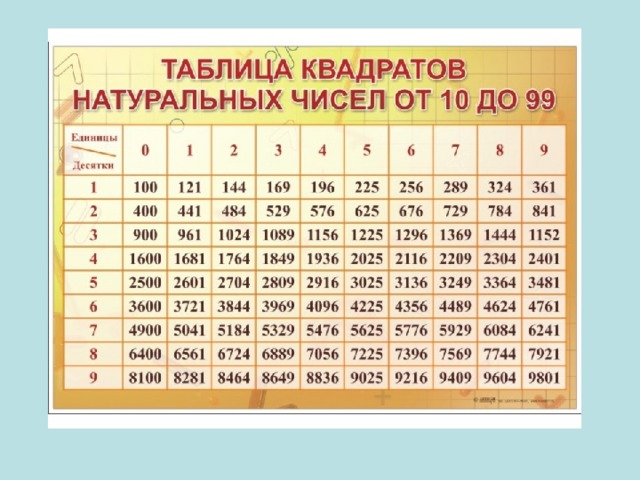
• Таблица квадратов натуральных чисел

• Презентация “Квадрат и куб числа”.

• Электронный тест “Квадрат и куб числа”.

Ход урока

1. Организационный момент.

- Здравствуйте.

- Какие вопросы по домашнему заданию?

- Сегодня на уроке мы сначала восхитимся нашими умениями вычислять, для этого проведем устный счет.

2. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний.

Устный счет. “Круговые” примеры. (Cлайд 1) 

Вычислите устно:

А) 35+35+35+35+35; б) 51+51+51+51; в)7*13+37*7; г)150+270/90; д)204-104-65; е)175/25;

ж)350-50*4; з)153/3

- В каких выражениях можно одно действие заменить другим?

3. Ознакомление с новым материалом.

- На доске записаны выражения. (Cлайд 2)

2 + 2 + 2 + 2 + 2 и 2 · 2 · 2 · 2 · 2

- Как вы думаете?  Что общего у них? Чем они отличаются?

- Мы с вами уже повторили, как сумму 2 + 2 + 2 + 2 + 2 записать короче.

2 + 2 + 2 + 2 + 2=2 · 5.

• Что показывает число 2?

• Что показывает число 5?

- А как вы думаете, можно ли произведение 2 · 2 · 2 · 2 · 2 записать короче?

Проблема нашего урока состоит именно в том, записать данное выражение короче. Оказывается можно. Вот как: 2 · 2 · 2 · 2 · 2 =2 ⁵.

400 лет назад французский математик Рене Декарт предложил именно такой способ записи произведения нескольких одинаковых множителей. (Слайд 3)

Тема нашего урока “Степень числа. Квадрат и куб числа”. (Cлайд 4)

- Запись 2⁵ читают “два в пятой степени”. (Запись в тетрадь и проговорить). (Cлайд 5)

• 2 – основание степени;

• 5 – показатель степени;

• 2 ⁵ – степень.

- Прочитайте выражения, назовите в каждом основание и показатель степени: (слайд 6)

6⁷, 12³, 4¹⁰, 15², 3⁵, 8¹

- Запишем произведения в виде степени :

а) 4 · 4 · 4; б) 3 · 3 · 3; в) 2 · 2 · 2 · 2 · 2 · 2.

Г) 5* 5 д) 7* 7* 7* 7 е)6*6

Рассмотрим некоторые свойства степени: (слайд 8)

- Вторую степень числа принято называть иначе.

- Произведение 5 · 5 называют квадратом числа 5 и обозначают 5².

n² = n · n (Чтение правила в учебнике).

- Рассмотрим таблицу квадратов первых десяти натуральных чисел. Как получены числа второй строки?( слайд 10)

- Третья степень числа также имеет свое особое название.

- Произведение 7 · 7 · 7 называют кубом числа 7 и обозначают 7³.

n³ = n · n · n (чтение правила в учебнике). (Слайд 9)

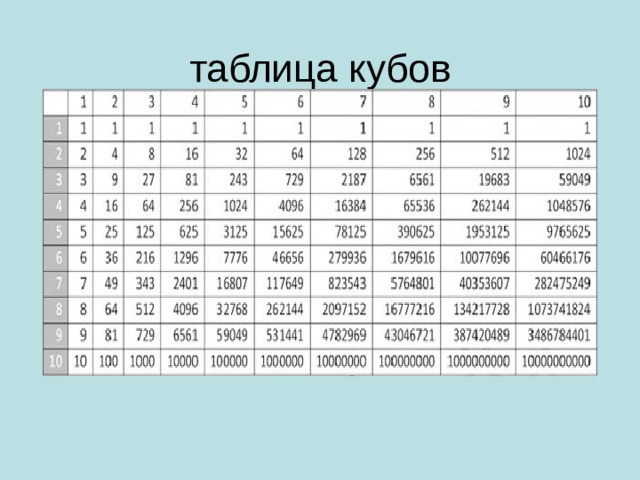
- Рассмотрим таблицу кубов первых десяти натуральных чисел. Как получены числа второй строки? (Слайд 11)

- Квадрат числа в пределах 10 вычислить легко, это примеры из таблицы умножения, а вот квадрат чисел в пределах 20 помещены на форзаце учебника. Откройте эту таблицу. Чему равен квадрат 11, 12, 13. Для удобства здесь размещена таблица кубов, чтобы не искать ее в учебнике. Рассматриваю решение примеров 1 и 2 из учебника.

4. Первичное осмысление и закрепление связей и отношений в объектах изучения.

1. №653 (а-е) 654 (а-е), (655, 656)

Закрепление изученного материала.

2. Тест (в электронном виде). (имеется отдельно в виде слайда)

5. Постановка домашнего задания. (Слайд 12)

Дома прочитайте п.16, выучите два правила, выполните задание

№ 653 (ж-м), №666

6. Подведение итогов урока. (Слайд 13)

Назовите основание степени и показатель степени:

3⁴, 5⁷, 9³, 15⁸, 13².

• Что такое “квадрат числа”?

• Что такое “куб числа”?

С учетом всей работы на уроке выставляются отметки за урок.

Подготовил рук-ль МО: Фаталиев Р.Г.

Логические задачи

Задача 1

Пятеро каменщиков вначале рабочей недели получили равное количество кирпича. Когда трое из них израсходовали по 326 кирпичей, то у них осталось столько кирпичей, сколько вначале получили другие два каменщика. Сколько всего кирпичей получили каменщики вначале недели?

• Решение

• По условию задачи каменщиков 5, значит частей тоже 5. Три части из пяти у каменщиков, которые израсходовали по 326 кирпичей, остальные две части у двух других каменщиков. Разница между этими частями одна пятая, которая равна:

• 326 · 3 = 978(кирпичей);

• далее вычисляем, сколько всего было кирпичей:

• 978 · 5 = 4890.

• Ответ: вначале недели каменщики получили всего 4890 кирпичей.

Задача 3

Из автобуса на остановке вышло 6 пассажиров, а вошло 11. На следующей остановке вышло 8, вошло 9. Сколько пассажиров стало в автобусе, если вначале в автобусе было 24 пассажира?

• Решение

• 1) 24 – 6 + 11 = 29 (пассажиров) стало в автобусе после первой остановки;

• 2) 29 - 8 + 9 = 30 (пассажиров).

• Ответ: в автобусе стало 30 пассажиров.

Задача 6

В железнодорожной кассе стоимость билетов для двух детей и трех взрослых составила 900 рублей. Сколько стоит билет для одного ребенка, если взрослый билет стоит 200 рублей?

• Решение

• 1) 200 · 3 = 600 (р.) общая стоимость взрослых билетов;

• 2) 900 – 600 = 300 (р.) общая стоимость детских билетов;

• 3) 300 : 2 = 150 (р.)

• Ответ: один детский билет стоит 150 рублей.

Задача 7

Велосипедист каждый день преодолевал по 45 км. Сколько километров в день нужно преодолевать велосипедисту, чтобы вернуться обратно за 9 дней, если все путешествие у него заняло 10 дней?

• Решение

• 1) 45 + 10 = 450 (км) всего преодолел велосипедист;

• 2) 450 : 9 = 50 (км).

• Ответ: велосипедисту нужно преодолевать по 50 км в день.

Задача 8

Папе 42 года, он на 29 лет моложе дедушки и в 3 раза старше сына. Сколько лет дедушке и сколько лет сыну?

• Решение

• 1) 42 + 29 = 71 (год) дедушке;

• 2) 42 : 3 = 14 (лет) сыну.

• Ответ: сыну 14 лет, дедушке 71 год.

Вычислите устно:

35+35+35+35+35

51+51+51+51

150+270:90

7х13+37х7

204-104-65

175:25

350-50х4

153:3

2+2+2+2+2

= 2х5

ПОДУМАЙТЕ!

5

2х2х2х2х2

= 2

400 лет назад французский математик Рене Декарт предложил такой способ записи произведения нескольких одинаковых множителей

ТЕМА УРОКА:

5

Запись 2 читают « два в пятой степени».

ЗАПОМНИТЕ!

• 2 – основание степени;

• 5 – показатель степени;

• 2 - степень.

5

Прочитайте выражения, назовите в каждом основание и показатель степени:

10

3

7

МОЛОДЦЫ!

12 ;

4 ;

6 ;

2

5

1

8 .

15 ;

3 ;

Общий вид

a n – cтепень

a – основание степени

n – показатель степени

a n = а*а*а*…*а

n раз

Свойства степени

• Нулевая степень любого числа равна нулю.
• Первая степень любого числа равна самому числу:
• Вторую степень числа называют «квадратом»:
• Третью степень числа называют «кубом»:

Общий вид квадрата и куба числа: n 2  = n · n   n 3  = n · n · n 

таблица кубов

Постановка домашнего задания. Дома прочитайте п.16, выучите два правила, выполните задание № 653 (ж-м), №666

Подведение итогов урока. Назовите основание степени и показатель степени: 3 4 , 5 7 , 9 3 , 15 8 , 13 2 . Что такое “квадрат числа”? Что такое “куб числа”?