Относительность движения.
Цели урока: продолжить формирование знаний об относительности движения; доказать. Что траектория, перемещение, координаты, скорости – понятия относительные.
Ход урока
I. Проверка домашнего задания, повторение
Двое учеников выписывают на доске решения домашних задач.
II. Новый материал
Допустим, что человек, неподвижно сидящий на движущейся платформе, наблюдает за арбузом, лежащим на той же платформе. Естественно, что он мысленно свяжет систему отсчета с платформой. Для него (или в системе отсчета, связанной с платформой) арбуз находится в покое.
В это же время человек, находящийся у полотна железной дороги, мысленно связав систему отсчета с землей, увидит, что арбуз движется.
Рассмотренный пример показывает, что одно и тоже тело движется в разных системах отсчета по-разному: в системе отсчета, связанной с платформой, арбуз находится в покое, а относительно системы отсчета, связанной с землей, движется. Поэтому движение относительно.
Ребенок, впервые попавший на берег реки во время ледохода, спросил: «На чем это мы едем?» (Ребенок «выбрал» в качестве тела отсчета плывущую по реке льдину.) Находясь в покое относительно берега, ребенок двигался вместе с берегом относительно «выбранной» им системы отсчета - льдина.
В стихотворении И.А. Бунина «В поезде» есть такие строки: Вот мост железный над рекой Промчался с грохотом под нами ...
- Что писатель-пассажир выбрал за систему отсчета? (Писатель «выбрал» систему отсчета, связанную с поездом. Поэтому поезд условно считается неподвижным. Относительно этой системы отсчета мост в самом деле движется.)
Обратите внимание, в двустишии отмечается также, что не только движение тела, но и его положение относительно: мост расположен под поездом, но над рекой.
Еще один пример относительности движения и покоя. Всем, наверное, известно, как трудно, находясь в вагоне поезда и глядя в окно на проходящий мимо по соседнему пути поезд, выяснить, какой из поездов движется, а какой покоится. Строго говоря, если видеть только соседний вагон и не видеть землю, строения и т.д., то узнать, какой из поездов движется прямолинейно равномерно, а какой - покоится, невозможно. Утверждение пассажиров, что его поезд движется, а другой стоит, будет справедливо для обоих поездов, т.к. движение и покой относительны.
Пример 1
П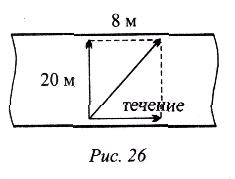 ловец пересек реку шириной 20 м, выдерживая курс поперек реки (рис.). В то же время течение реки его снесло на расстояние 8 м. Каков модуль суммарного перемещения пловца?(Ответ: модуль суммарного перемещения
ловец пересек реку шириной 20 м, выдерживая курс поперек реки (рис.). В то же время течение реки его снесло на расстояние 8 м. Каков модуль суммарного перемещения пловца?(Ответ: модуль суммарного перемещения 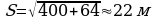 )
)
Пример 2
Пассажир, находящийся в вагоне поезда, проходит по направлению его движения 20 м. Каков модуль перемещения пассажира относительно Земли, если за то же время поезд прошел 200 м? Все движения прямолинейные. А если пассажир идет против поезда? (Ответы: 220 м и 180 м.)
Пример 3
В условиях примера 2 определите, каков модуль перемещения пассажира, поезда и земли в системе отсчета, связанной с пассажиром? (S= 0, Sn = 20 м,S3 = 220 м, S3 = 180 м).
Понятие того, что движение одного и топик тела можно рассматривать в разных системах отсчета, сыграло огромную роль в развитии взглядов на строение Вселенной.
Идея о вращении планет вокруг Солнца (гелиоцентризм) возникла еще в Древней Греции (Гераклий Понтийский, Аристарх; Самосский…), но в дальнейшем почти на двадцать веков была забыта и отчасти из-за противоречивости ощущений и утверждения о движении Земли; отчасти из-за преследований со стороны церкви. Николай Коперник, живший в XVI в., получил отличное образование в университетах Польши и Италии (математика, астрономия, право, языки, медицина). Почти всю свою жизнь, он провел в должности каноника Всермийской иерархии, занимался устройствам самых разнообразных дел, свободное время отдавал астрономии. Титаническая работа, которая сопровождалась, наблюдениями и вычислениями продолжалась в течение почти двадцати лет. Книга Коперника «О вращении небесных сфер» вышла в 1543 г. В этом труде земной шар низводился в ранг рядовой планеты, движущейся, как и остальные, по орбите вокруг Солнца и вращающейся вокруг оси. Книгу внесли в «Индекс запрещенных».
III. Решение задач
Задача 1
Эскалатор метро движется со скоростью 0,75 м/с. Найти время, за которое пассажир переместился на 20 м относительно земли, если он сам идет в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета, связанной с эскалатором, (Ответ: 20 с )
Задача 2
Два поезда движутся навстречу друг другу со скоростями 72 км/ч и 54 км/ ч. Пассажир, находящийся в первом поезде, замечаем, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда?
| Дано: υ1 = 72 км/ч υ2 = 54 км/ч t = 14 c l - ? | Решение: 72 км/ч = 20 м/с; 54 км/ч = 15 м/с Суммарная скорость движения поездов относительно друг друга: υ = υ1 + υ2 = 20 м/с + 15 м/с = 35 м/с l = υt = 35 м/с · 14 с = 490 м Ответ: l = 490 м |
Задача 3
Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 1 минуты. По неподвижному эскалатору пассажир поднимается за 3 минуты. Сколько времени будет подниматься идущий вверх пассажир по движущемуся эскалатору. (Ответ: 45 с.)
Задача 4
Самолет движется относительно воздуха со скоростью 50 м/с. Скорость ветра относительно земли 15 м/с. Какова скорость самолета относительно земли, если он движется по ветру? Против ветра? Перпендикулярно направлению ветра? (Ответ: υ1 = 65 м/с, υ2 = 35 м/с, υ3 = 52 м/с.)
Домашнее задание:
§ 9 (с. 34-38);
2. Упражнение 9 (с. 38-39)
3. Решить задачу (для желающих): Скорость катера перпендикулярна скорости реки υр и относительно берега равна υк1 = 4 м/с. Чему равна скорость реки, если скорость катера относительно воды равна υк2 = 5 м/с? (Ответ: υ = 3 м/с.)





 ловец пересек реку шириной 20 м, выдерживая курс поперек реки (рис.). В то же время течение реки его снесло на расстояние 8 м. Каков модуль суммарного перемещения пловца?(Ответ: модуль суммарного перемещения
ловец пересек реку шириной 20 м, выдерживая курс поперек реки (рис.). В то же время течение реки его снесло на расстояние 8 м. Каков модуль суммарного перемещения пловца?(Ответ: модуль суммарного перемещения 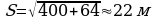 )
)









