МБОУ СОШ №1 с. Кизляр
План- конспект открытого урока
по математике в 11 классе
«Подготовка к ЕГЭ. Решение сложных комбинированных уравнений»
Урок разработала и провела:
Магометова Х. Н.,
учитель математики
МБОУ СОШ №1 с. Кизляр
Апрель 2021 г
Тип урока: семинарское занятие.
Цели урока:
Познавательные: повторить и обобщить изученный за курс средней школы материал по математике, закрепить навыки решения сложных уравнений различными методами.
Развивающие: развивать ключевые коммуникативные компетенции, речь, внимание, память, логическое мышление, умение обобщать, делать выводы, развивать навыки самоконтроля и творческие способности учащихся.
Воспитательные: совершенствовать навыки этичного межличностного общения, сознательное отношение к математике; активизировать познавательную деятельность в коллективе, формировать навыки сотрудничества в решении поисковых задач, воспитывать у учащихся морально-ценностные чувства.
Задачи урока:
Систематизировать теоретические знание по теме.
Развивать умение работать с заданиями ЕГЭ.
Совершенствовать навыки решения сложных уравнений различными методами.
Ход урока:
I Организационный момент:
а) готовность класса к уроку;
б Слово учителя: Ребята, сегодня у нас необычный урок. Мы проверим наши знания, уровень нашей подготовки к сдаче ЕГЭ. И я хочу начать сегодняшний урок с притчи.
- Учитель, я уже целый год живу у тебя, но до сих пор выполняю только работы по хозяйству. Когда ты будешь меня учить? Разве я для этого пришёл к тебе в ученики, скажи?
- Имей терпение, - ответил учитель, - ещё не пришло время. Иди в нижнюю долину и посади дерево, вырасти его, а я подумаю.
Долгий и тяжёлый путь проделал ученик, пока спустился в долину. По дороге он выкопал маленький саженец и посадил его. С той поры, дважды в день он проходил опасный путь, между хижиной и долиной, чтобы полить деревце. Изо дня в день, он присматривал за деревом. Так прошёл год. Усилия его не пропали даром. Дерево выросло высоким и крепким. Однажды на рассвете, он вышел из хижины и увидел своего учителя, сидящего у ручья под деревом.
- Учитель! – обрадовался юноша. – Как я счастлив вновь увидеть тебя! Я должен извиниться перед тобой, что не смог стать твоим учеником, обманув твоё доверие! Ты подумал, что я слаб, когда я остался жить в долине. Но я должен был заботиться о своём деревеИ теперь, ты вряд ли возьмёшь меня обратно…
Выслушав пылкую речь юноши, старик сказал ему: - Именно в этот год, ты вместе с деревом взращивал такие качества своего характера, которые тебе помогут постигать знания.
Твоё дерево говорит о твоей готовности. Посмотри!
Ответственность ты имел, но только по необходимости, Был нетерпелив и эмоционален, как переплетенные побеги саженца. Чтобы обрести знания, нужна, прежде всего, дисциплина.
Ибо корни дерева – твоя ответственность,
ствол дерева – твоё терпение,
ветви дерева – спокойствие,
а листья – знания!
И вам я желаю такого же упорства и терпения, чтобы хорошо подготовиться к ЕГЭ и успешно его сдать.
А теперь приступим к выполнению заданий.
Проверка дз.
Дать определение уравнения и его корня, равносильности двух уравнений.
Ответ:
Арифметическое выражение, содержащее неизвестную переменную и знаки равенства называют уравнением. Значение переменной, превращающее уравнение в верное равенство, называют корнем уравнения. Два уравнения называют равносильными, если любой корень первого уравнения является корнем второго уравнения и любой корень второго уравнения является корнем первого уравнения.
Дать определение равносильности преобразования уравнения и перечислить основные равносильные преобразования.
Ответ:
Замену одного уравнения другим, равносильным ему уравнением называют равносильным преобразованием уравнения.
Равносильными преобразованиями уравнения являются:
перенос члена уравнения с противоположным знаком из одной части уравнения в другую;
умножение (деление) обеих частей уравнения на отличную от нуля число;
возведение уравнения в нечетную степень;
извлечение корня нечетной степени с обеих частей уравнения:
логарифмирование показательного уравнения;
применение тождеств, т. е равенств, справедливых для любого числа.
Рассказать, какие равносильные преобразования нужно выполнить, чтобы решить следующие уравнения

 ;
;
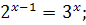

Дайте определение уравнения – следствия и перечислите преобразования, приводящие к уравнению следствия.
Ответ:
Пусть даны два уравнения. Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют уравнением- следствием первого.
Замену уравнения другим уравнением, которое является его следствием, называют переходом к уравнению- следствию.
При переходе к уравнению- следствия возможно появление лишних корней, посторонних для исходного уравнения, поэтому проверка полученных корней является обязательной частью решения уравнения.
Преобразованиями, приводящими к уравнению- следствия является:
возведение уравнения в четную степень;
потенцирование логарифмического уравнения;
освобождение уравнения от знаменателя;
приведение подобных членов;
применение формул (тригонометрических, логарифмических и других).
Расскажите, каким способом приводится следующие уравнения к уравнению – следствия.

 ;
;




 ;
;


 .
.
Карточки имеются у каждого ученика на парте.
Сложные уравнения можно решить, приводя их к системам. Правила перехода от уравнений к равносильным системам:
1.
2.
3.
4.
5.
6.
7.
М-область существования 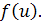
8.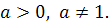
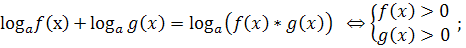
9.
10.
11. 
Работа в группах.
Запишите системы, равносильные уравнениям. (Работы выполняют на листочках)..
1.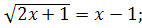
2.
3.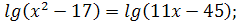
4.
5.
6.
7.
8.
9.
10.
11.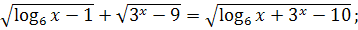

Очень часто можно встретить уравнение, которое имеет дополнительное условие, например:

Как можно упростить решение такого типа уравнения?
Разбор решения на доске.
Ответ:
Учитывая, что левая часть уравнения неотрицательное число получаем  значит, множество решений данного уравнения есть
значит, множество решений данного уравнения есть . Левая часть уравнения для любого
. Левая часть уравнения для любого  есть отрицательное число, значит, рассматривается только одно уравнение
есть отрицательное число, значит, рассматривается только одно уравнение  . Решается квадратное уравнение, находим
. Решается квадратное уравнение, находим  и выбираем те, которые принадлежат множеству М.
и выбираем те, которые принадлежат множеству М.
Самыми сложными считаются уравнения с параметром. Дайте определение уравнения с параметром. Давайте рассмотрим несколько таких уравнений с использованием свойств функций:
а)
 имеет ровно три корня.
имеет ровно три корня.
Ответ:
Для каждого значения a рассмотрим функцию
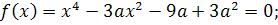
Она определена на множестве R, четная, поэтому, если  - корень уравнения, то
- корень уравнения, то  - тоже является корнем уравнения.
- тоже является корнем уравнения.
Уравнение (1) имеет три корня тогда и только тогда, когда оно имеет 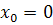 и еще два отличных от нуля корня, отличающихся знаками.
и еще два отличных от нуля корня, отличающихся знаками.
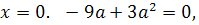 получаем:
получаем: 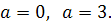
При  уравнение примет вид
уравнение примет вид  у уравнения только один корень.
у уравнения только один корень.
При  уравнение имеет вид
уравнение имеет вид  . Это уравнение имеет три корня
. Это уравнение имеет три корня  Ответ:3
Ответ:3
Видеоурок.
Максимум за выполнение данного задания(18 задание) можно получить 4 балла.
В задачах с параметром допускают весьма разнообразные способы решений. Наиболее распространенными из них являются;
Чисто алгебраический способ решения;
-способ решения,основанный на построении и исследовании геометрической модели данной задачи;
-функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.
Критерии оценивания:
|
| Обоснованно получен верный ответ | 4 балла |
|
| С помощью верного рассуждения получены оба верных значения параметра, но -или в ответ включены и одно-два неверных значения; -или решение недостаточно обосновано. | 3 балла |
|
| С помощью верного рассуждения получено хотя бы одно верное значение параметра | 2 балла |
|
| Задача сведена к исследованию: -или взаимного расположения трех окружносей; -или двух квадратных уравнений с параметром. | 1 балл |
|
| Решение не соответствует ни одному из критериев, перечисленных выше | О баллов |
Выполнения тренировочных упражнений на закрепление навыков и умений решать уравнения.

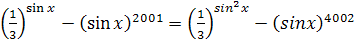 ;
;

VI Домашнее задание:
Разбор заданий типа С с индивидуальных карточек с сайта www.ege.edu.ru Банк заданий на доске.
Карточка №1
С1.(В13) 
Карточка №2
C1.(B1) 
Карточка №3
C1.(B12) 
Карточка №4
C1.(B19) 
Карточка №5
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка №6
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка № 7
Найти наибольший корень уравнения:
 .
.
Карточка № 8
Найти значение р, при которых уравнение
 не имеет решений.
не имеет решений.
Карточка №9
Решить уравнение
Повторить теорию по темам:
Уравнения-следствия.
Равносильность уравнений системам.
Равносильность уравнений на множествах.
VII Подведение итогов урока.
Оцените вашу работу на уроке.
Сколько баллов вы набрали?
К какому выводу пришли?
Лист самооценки работы учащегося
---------------------------------------------------------------------------------(Ф.И. учащегося)
---------------------------------------------------------------------------------(тема урока)
| Мой вклад… | Баллы |
|
| 1(плохо) | 2(слабо) | 3(хорошо) | 4(отлично) |
| В поисках материала по теме |
|
|
|
|
| В теоретическом изучении материала |
|
|
|
|
| В решении примеров |
|
|
|
|
| В групповой работе |
|
|
|
|
| В защите работ, анализе решений |
|
|
|
|
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
Лист самооценки работы учащегося
---------------------------------------------------------------------------------(Ф.И. учащегося)
---------------------------------------------------------------------------------(тема урока)
| Мой вклад… | Баллы |
|
| 1(плохо) | 2(слабо) | 3(хорошо) | 4(отлично) |
| В поисках материала по теме |
|
|
|
|
| В теоретическом изучении материала |
|
|
|
|
| В решении примеров |
|
|
|
|
| В групповой работе |
|
|
|
|
| В защите работ, анализе решений |
|
|
|
|
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5





























