Россия, Нижегородская область Гагинский МО село Исупово
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 25.12.2023 11:12
Малафеева Татьяна Николаевна
Учитель математики, заместитель директора по ВР
56 лет
7 871
6 080 
Местоположение
Специализация
Презентация по теме Линейная функция
Категория:
Математика
07.08.2017 00:49
Просмотр содержимого документа
«Презентация по теме Линейная функция»
МБОУ Исуповская СШ
Команда «Ровесник»
Линейная функция
Функция (от лат. functio – исполнение, осуществление) – зависимость одних переменных величин от других.
Линейное уравнение имеет вид:
ах + by + c = 0
y = kx + m
Частный вид линейного уравнения с двумя
переменными называется линейной функцией.
y – независимая переменная
х – зависимая переменная
Графиком линейной функции y = kx + m есть прямая.
Функция y = kx + m называется возрастающей , если
большему значению аргумента соответствует
большее значение функции (двигаясь по графику
функции, мы поднимаемся вверх ).
Функция y = kx + m называется убывающей , если
большему значению аргумента соответствует
меньшее значение функции (двигаясь по графику
функции, мы опускаемся вниз ).
0, то линейная функция у = kx + b возрастает. Если k = 0, то линейная функция у = kx + b параллельна оси абсцисс (или совпадает с ней). " width="640"
Величина k определяет наклон графика
функции y = kx + m
Если k
у = kx + b убывает.
Если k 0, то линейная функция
у = kx + b возрастает.
Если k = 0, то линейная функция
у = kx + b параллельна оси абсцисс
(или совпадает с ней).
0, то линейная функция у = kx + b, возрастает. Точка пересечения с осью оу: (0; 3) т. е. при т = 3 " width="640"
y
Пример 1
у = 2х + 3
Построить график функции
у = 2х + 3, найти точку
пересечения с осью оу.
(1; 5)
5
k = 2
1. Составим таблицу значений:
(0; 3)
3
х
0
у
3
1
5
O
(0; 3), (1; 5)
2. Получим точки:
x
1
3. Построим эти точки и
через них проведем прямую.
Если k 0, то линейная функция
у = kx + b, возрастает.
Точка пересечения с осью оу: (0; 3) т. е. при т = 3
y
Пример 2
у = -2х + 1
Построить график функции
а) у = -2х + 1 х -3; 2
7
(-3; 7)
1. Составим таблицу значений:
х
-3
у
2
7
-3
k = -2
2. Получим точки:
(-3; 7), (2; -3)
3. Построим эти точки и
через них проведем прямую.
O
x
1
-3
2
(2; -3)
Если k
у = kx + b убывает.
-3
Точка пересечения с осью оу: (0; 1) т. е. при т = 1
y
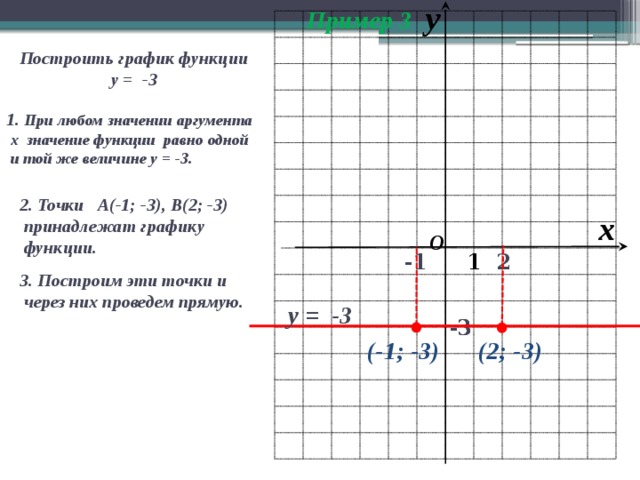
Пример 3
Построить график функции
у = -3
1. При любом значении аргумента
х значение функции равно одной
и той же величине у = -3.
2. Точки А(-1; -3), В(2; -3)
принадлежат графику
функции.
x
O
1
-1
2
3. Построим эти точки и
через них проведем прямую.
у = -3
-3
-3
(2; -3)
(-1; -3)
8
Пусть т = 0, тогда y = kx
- частный вид линейной функции называют
прямой пропорциональной зависимостью
(прямой пропорциональностью).
k
– коэффициент пропорциональности
Графиком прямой пропорциональности y = kx есть прямая, проходящая через начало координат.
При х = 0 величина у = 0 при любом значении k.
Следовательно график проходит через точку
(0; 0) – начало координат
Поэтому для построения графика функции
у = k х
достаточно взять еще только одну точку.
y
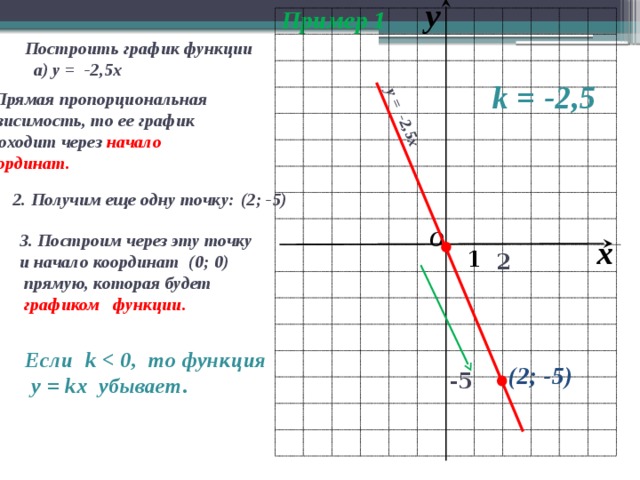
Пример 1
у = -2,5х
Построить график функции
а) у = -2,5х
k = -2,5
1. Прямая пропорциональная
зависимость, то ее график
проходит через начало
координат.
2. Получим еще одну точку:
(2; -5)
O
3. Построим через эту точку
и начало координат (0; 0)
прямую, которая будет
графиком функции.
x
1
2
Если k
у = kx убывает.
(2; -5)
-5
0, то прямая располагается в первом и третьем координатных углах. " width="640"
y
Пример 2
у = х
у = 2х
у = -2х
Построить графики функций
в одной системе координат
а) у = х; б) у = 2х; в) у = -2х
k = 2
1. Прямая пропорциональная
зависимость, то все графики
проходят через начало
координат.
k =1
k = -2
I
II
В(1; 2)
2. Получим еще по одной точке:
А(1; 1)
2
1
x
а) А(1; 1), б) В(1; 2), в) С(1; -2)
O
1
3. Построим через эти точки
и начало координат (0; 0)
прямые, которые будут
графиками функций.
III
IV
С(1; -2)
-2
Если k
координатных углах.
Если k 0, то прямая располагается в первом и третьем
координатных углах.
Вывод:
k
– коэффициент пропорциональности
k
– характеризует расположение графика
функции и скорость изменения функции
(угол наклона графика к оси абсцисс)
Поэтому коэффициент k называют
угловым коэффициентом.
Взаимное расположение графиков
линейных функций
Возможно три случая их взаимного расположения:
а) или прямые пересекаются;
б) или прямые параллельны;
в) или прямые совпадают.
Пусть даны две линейные функции
у = k ₁x + m₁ и у = k₂x + m₂
Теорема:
Если угловые коэффициенты k ₁ = k₂, то прямые параллельны (или совпадают при т₁ = т₂)
Если угловые коэффициенты k ₁ ≠ k₂ , то прямые пересекаются.
Линейные функции
Алгебраическое условие
у = k ₁x + m₁
1) k ₁ = k₂, т₁ ≠т₂
Геометрический вывод
у = k ₂x + m₂
2) k ₁ = k₂, т₁ = т₂
Прямые
k ₁ ≠ k₂
Прямые
у = k ₁x + m₁ и
у = k ₁x + m₁ и
Прямые
у = k₂x + m₂ - параллельны
у = k ₁x + m₁ и
у = k₂x + m₂ - совпадают
у = k₂x + m₂ - пересекаются
y
Пример 1
у = -2х + 1
у = 2х + 3
Построить графики функций
у = -2х + 1 и у = 2х + 3
7
(-3; 7)
- Составим таблицу значений
для у = -2х + 1
5
(1; 5)
х
-3
у
7
2
-3
(0; 3)
3
(-3; 7), (2; -3)
2. Получим точки:
2
3. Построим эти точки и
через них проведем прямую.
O
x
1
1
2
-3
-0,5
4. Составим таблицу значений
для у = 2х + 3
х
у
0
3
1
5
(2; -3)
-3
(0; 3), (1; 5)
5. Получим точки:
6. Построим эти точки и
через них проведем прямую.
Точка пересечения графиков
(-0,5; 2)
y
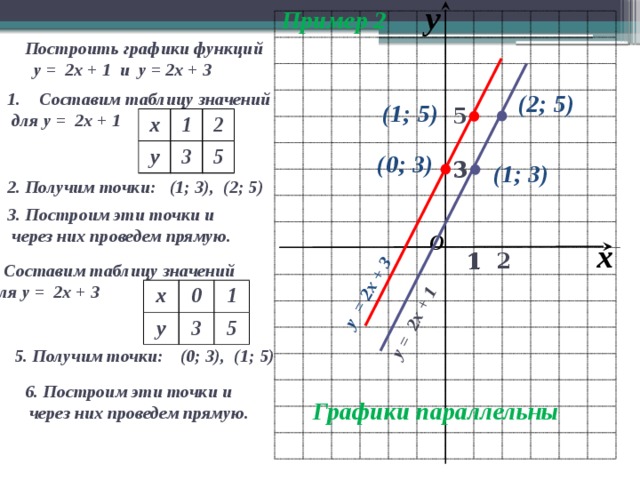
Пример 2
у = 2х + 1
у = 2х + 3
Построить графики функций
у = 2х + 1 и у = 2х + 3
(2; 5)
- Составим таблицу значений
для у = 2х + 1
(1; 5)
5
х
1
у
3
2
5
(0; 3)
3
3
(1; 3)
(1; 3), (2; 5)
2. Получим точки:
3. Построим эти точки и
через них проведем прямую.
O
x
2
1
1
1
4. Составим таблицу значений
для у = 2х + 3
х
у
0
3
1
5
(0; 3), (1; 5)
5. Получим точки:
6. Построим эти точки и
через них проведем прямую.
Графики параллельны
y
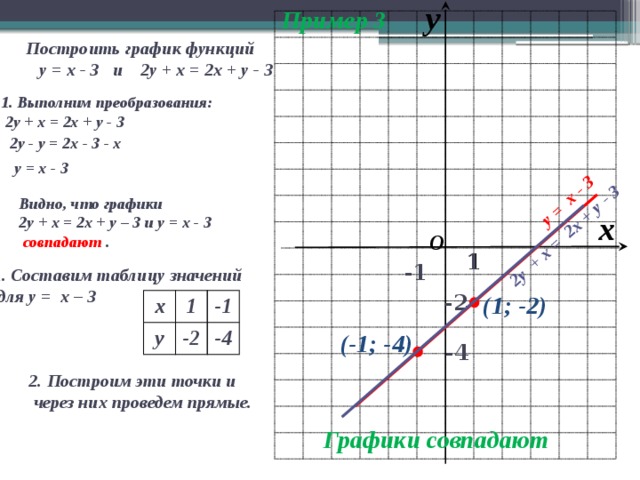
Пример 3
у = х - 3
2у + х = 2х + у - 3
Построить график функций
у = х - 3 и 2у + х = 2х + у - 3
1. Выполним преобразования:
2у + х = 2х + у - 3
2у - у = 2х - 3 - х
у = х - 3
Видно, что графики
2у + х = 2х + у – 3 и у = х - 3
совпадают .
x
O
1
1
-1
1. Составим таблицу значений
для у = х – 3
(1; -2)
-2
х
у
1
-2
-1
-4
(-1; -4)
-4
2. Построим эти точки и
через них проведем прямые.
Графики совпадают
Многие реальные ситуации описываются математическими моделями , представляющими собой линейные функции.
Первая ситуация. На складе было 500 т угля. Ежедневно стали подвозить по 30 т угля. Сколько угля будет на складе через 2, 4, 10 дней?
Если пройдет х дней, то количество у угля на складе (в тоннах) выразится формулой у =500 + 30х. Таким образом, линейная функция у = З0x + 500 есть математическая модель ситуации.
Вторая ситуация. Турист проехал на автобусе 15 км от пункта А до Б, а затем продолжил движение из пункта В в том же направлении, но уже пешком, со скоростью 4 км/ч. На каком расстоянии от А будет турист через 2 ч, через 4 ч, через 5 ч ходьбы?
Математической моделью ситуации является линейная функция
у=15 + 4х, где х — время ходьбы (в часах), у — расстояние от А
(в километрах).
Команда «Ровесник»
Спасибо за внимание!
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
