Признаки равенства треугольников

Признаки равенства треугольников

Учитель Петрова А.А.

Понятие треугольник

• Треугольник  – это геометрическая фигура на плоскости, состоящая из трех сторон, которые образованы путем соединения трех точек, не лежащих на одной прямой. Для обозначения используется специальный символ – △

• Точки A, B и C – вершины треугольника.
• Отрезки AB, BC и AC – стороны треугольника, которые часто обозначаются в виде одной латинской буквы

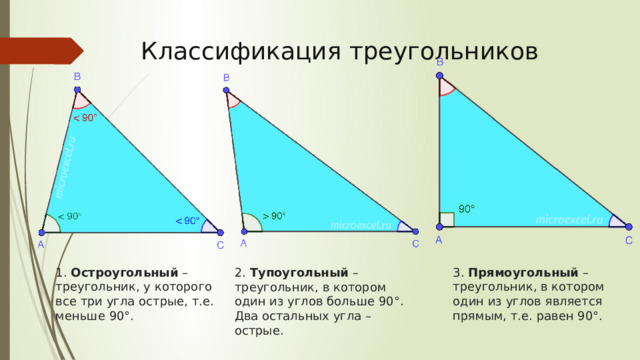
Классификация треугольников

1.  Остроугольный  – треугольник, у которого все три угла острые, т.е. меньше 90°.

3.  Прямоугольный  – треугольник, в котором один из углов является прямым, т.е. равен 90°. 

2.  Тупоугольный  – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

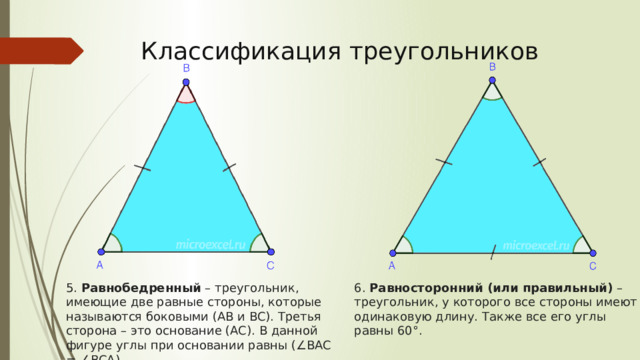
Классификация треугольников

5.  Равнобедренный  – треугольник, имеющие две равные стороны, которые называются боковыми (AB и BC). Третья сторона – это основание (AC). В данной фигуре углы при основании равны (∠BAC = ∠BCA).

6.  Равносторонний (или правильный)  – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

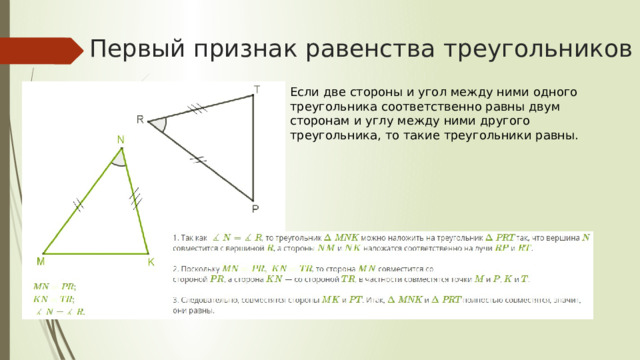
Первый признак равенства треугольников

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

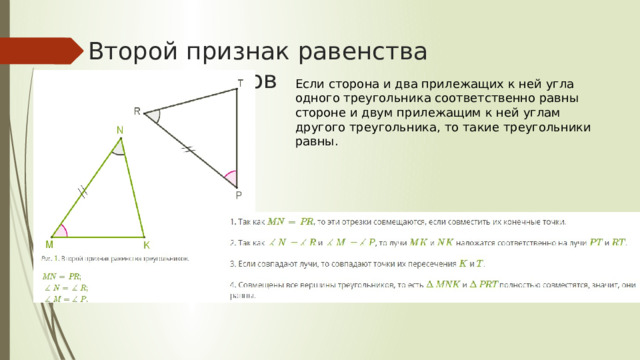
Второй признак равенства треугольников

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.