Проект "Применение игровых технологий на уроках математики"

МБОУ «НОВО- СНОПКОВСКАЯ ОСНОВНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»

Проект по математике

«Применение игровых технологий на уроках математики»

Выполнила учитель математики: ПУСТОВАЯ Е.Ю.

План

• Пояснительная записка.
• Цели и задачи.
• Функции математических игр.
• Требования к математическим играм.
• Виды математических игр.
• Древнекитайская мудрость.
• Игровые технологии.
• Математические ребусы и кроссворды.
• Фрагменты уроков с применением игровых технологий.

Пояснительная записка

• возникает у учащихся после длительного умственного труда на уроках. Игровые формы занятий или математические игры – это занятия, пронизанные элементами игры, соревнования, содержащие игровые ситуации.
• Математическая игра как форма работы играет огромную роль в развитии познавательного интереса у учащихся. Игра оказывает заметное влияние на деятельность учащихся. Игровой мотив является для них подкреплением познавательному мотиву, способствует активности мыслительной деятельности, повышает концентрированность внимания, настойчивость, работоспособность, интерес, создает условия для появления радости успеха, удовлетворенности, чувства коллективизма. В процессе игры, увлекшись, дети не замечают, что учатся. Игровой мотив одинаково действен для всех категорий учащихся, как сильных и средних, так и слабых. Дети с большой охотой принимают участие в различных по характеру и форме математических играх. Математическая игра резко отличается от обычного урока, поэтому вызывает интерес большинства учащихся и желание поучаствовать в ней. Так же следует заметить, что многие формы работы по математике могут содержать в себе элементы игры, и наоборот, некоторые формы работы могут быть частью математической игры. Введение игровых элементов разрушает интеллектуальную пассивность учащихся.

Пояснительная записка

•   Классификации игр . Игры классифицируют по различным признакам. выделяются игры с правилами (настольные; игры-состязания; подвижные игры на местности; компьютерные) и творческие игры (ролевые; игровое проектирование; компьютерные) в зависимости от творческой активности учащихся.  

ЦЕЛИ И ЗАДАЧИ:

• Главной целью применения игровых технологий  является развитие устойчивого познавательного интереса у учащихся через разнообразие применения математических игр.
•   Цели применения математических игр:
• Развитие мышления;
• Углубление теоретических знаний;
• Самоопределение в мире увлечений и профессий;
• Организация свободного времени;
• Общение со сверстниками;
• Воспитание сотрудничества и коллективизма;
• Приобретение новых знаний, умений и навыков;
• Формирование адекватной самооценки;
• Развитие волевых качеств;
• Контроль знаний;
• Мотивация учебной деятельности и др.
• Математические игры призваны решать следующие задачи:
• Образовательные:
• Способствовать прочному усвоению учащимися учебного материала;
• Способствовать расширению кругозора учащихся и др.
• Развивающие:
• Развивать у учащихся творческое мышление;
• Способствовать практическому применению умений и навыков, полученных на уроках и внеклассных занятиях;
• Способствовать развитию воображения, фантазии, творческих способностей и др.
• Воспитательные:
• Способствовать воспитанию саморазвивающейся и самореализующейся личности;
• Воспитать нравственные взгляды и убеждения;
• Способствовать воспитанию самостоятельности и воли в работе и др.

Математические игры выполняют различные функции:

• 1.     Во время математической игры происходит одновременно игровая, учебная и трудовая деятельность. Действительно, игра сближает то, что в жизни не сопоставимо и разводит то, что считается едино.
• 2.     Математическая игра требует от школьника, то чтобы он знал предмет. Ведь не умея решать задачи, разгадывать, расшифровывать и распутывать ученик не сможет участвовать в игре.
• 3.     В играх ученики учатся планировать свою работу, оценивать результаты не только чужой, но и своей деятельности, проявлять смекалку при решении задач, творчески подходить к любому заданию, использовать и подбирать нужный материал.
• 4.     Результаты игр показывают школьникам их уровень подготовленности, тренированности. Математические игры помогают в самосовершенствовании учащихся и, тем самым побуждают их познавательную активность, повышается интерес к предмету.
• 5.     Во время участия в математических играх учащиеся не только получают новую информацию, но и приобретают опыт сбора нужной информации и правильного ее применения.
•  

Математические игры выполняют различные функции:

• Игры и игровые формы включаются работу не только для того чтобы развлечь учеников, но и заинтересовать их математикой, возбудить у них стремление преодолеть трудности, приобрести новые знания по предмету. Математическая игра удачно соединяет игровые и познавательные мотивы, и в такой игровой деятельности постепенно происходит переход от игровых мотивов к учебным мотивам. Так на базе нашей школы проводятся следующие игры по математики:
• - Внеклассное занятие по математике "Путешествие в стану Умножалию";
•   -Игра «Самый умный »;
•   -«Путешествие с арифметикой;
•   -Вечер "Юный математик";
•   -Вечер: "В математике есть своя красота";
• - "Дорогами войны";
•   Викторина по истории геометрии "Что? Где? Когда?";
• Игра "Кто хочет стать отличником?";
•   Вечер "Удивительный мир чисел";
• - «Следствие ведут знатоки», и др.

Математические игры выполняют различные функции:

• Математическая игра помогает закреплять и расширять предусмотренные школьной программой знания, умения и навыки. Ее настоятельно рекомендуется использовать на внеклассных занятиях и вечерах. Но эти игры не должны восприниматься детьми как процесс преднамеренного обучения, так как это разрушило бы саму сущность игры. Природа игры такова, что при отсутствии абсолютной добровольности, она перестает быть игрой.
• В современной школе математическая игра используется в следующих случаях: в качестве самостоятельной технологии для освоения понятия, темы или даже раздела учебного предмета; как элемент более обширной технологии; в качестве урока или его части; как технология внеклассной работы .

Требования к игровым формам занятий:

• . К участникам математической игры должны предъявляться определенные требования в отношении знаний. В частности, чтобы играть – надо знать. Это требование придает игре познавательный характер.
• Правила игры должны быть такими, чтобы учащиеся проявили желание поучаствовать в ней. Поэтому игры должны разрабатываться с учетом возрастных особенностей детей, проявляемых ими интересов в том или ином возрасте, их развития и имеющихся знаний.
• Математические игры должны разрабатываться с учетом индивидуальных особенностей учащихся, с учетом различных групп учащихся: слабые, сильные; активные, пассивные и др. Они должны быть такими, чтобы каждый тип учащихся смог проявить себя в игре, показать свои способности, возможности, свою самостоятельность, настойчивость, смекалку, испытать чувство удовлетворенности, успеха.
• При разработке игры нужно предусмотреть более легкие варианты игры, задания для слабых учащихся и, наоборот, более сложный вариант для сильных учеников. Для совсем слабых учащихся разрабатываются игры, где не нужно думать, а нужна, лишь смекалка. Таким образом, можно привлечь больше учащихся к посещению внеклассных занятий по математике и тем самым способствовать развитию у них познавательного интереса

Требования к игровым формам занятий:

• Математические игры должны разрабатываться с учетом предмета и его материала. Они должны быть разнообразны. Многообразие видов математических игр поможет повысить эффективность работы по математике, послужит дополнительным источником систематических и прочных знаний.
• Таким образом, математическая игра как одна из форм работы по математике имеет свои цели, задачи и функции. Соблюдение же всех требований предъявляемых к математическим играм позволит добиться хороших результатов по привлечению большего числа учащихся в работу, возникновению у них познавательного интереса. Не только сильные учащиеся будут больше проявлять заинтересованность к предмету, но и слабые учащиеся начнут проявлять свою активность в учении.

Виды математических игр

• 1.По назначению различают  обучающие ,  контролирующие  и воспитывающие  игры. Также можно выделить  развивающие  и занимательные .
• 2.По массовости различают  коллективные  и  индивидуальные  игры.
• Игры подростков чаще всего принимают коллективный характер. Школьникам свойственно чувство коллективизма, у них есть желание участвовать в жизни коллектива в качестве его полноправного члена. Дети стремятся к общению со своими сверстниками, стремятся участвовать с ними в совместной деятельности. Поэтому использование коллективных и математических игр во внеклассной работе по математике так необходимо. Они привлекают не только сильных учеников, но и слабых, желающих поучаствовать в игре вместе со своими друзьями. Такие ученики, не проявляющие интереса к математике, в коллективной игре могут добиться успеху, у них появляется чувство удовлетворенности, интерес.
• С другой же стороны, сильные ученики предпочитают индивидуальные игры, так как они более самостоятельны. Они стремятся к самоанализу, самооценке, и поэтому у них возникает потребность проявить свои индивидуальные возможности, качества. Такие игры связаны обычно с умственным трудом, то есть являются интеллектуальными, в них учащиеся могут проявить свои умственные способности.
• Оба вида игр имеет свои особенности и возможности, поэтому о предпочтении какой-нибудь из них говорить нельзя.
• 3.По реакции выделяют  подвижные  и  тихие  игры.
• 4.По темпу выделяют  скоростные  и  качественные  игры.
• Некоторые математические игры должны принимать форму состязаний, соревнований между командами или на личное первенство, это обусловлено характерной чертой подростков, стремления к различным видам состязаний.

Виды математических игр

• Следует различать два вида состязаний. Во-первых, это игры, в которых победа достигается за счет скорости действий, но это без ущерба качеству решения задач. Например, задания на скорость выполнения вычислений, преобразований, доказательств теорем и т. д. Такие игры называются скоростными. Во-вторых, так же можно выделить игры, победа в которых достигается не за счет скорости выполнения заданий, а за счет качества его выполнения, правильности решения, безошибочности. Такие игры условно называют качественными.
• 5.Наконец, различают игры  одиночные  и  универсальные .
• К одиночным играм относят те игры, правила которых не допускают изменения содержания игры, они разработаны с учетом особенностей конкретного материала.
• Универсальные игры же, наоборот, позволяют менять свое содержание. Они разрабатываются по широкому кругу вопросов школьной программы, могут использоваться в различных целях, на различных внеклассных мероприятиях, и поэтому являются очень ценными.
• Знание   видов и требований математической игры позволяет не только развлечь учеников, но и заинтересовать их математикой, возбудить у них стремление преодолеть трудности, приобрести новые знания по предмету. Повысить уровень математического мышления, углубить теоретические знания и развить практические навыки учащихся, проявивших математические способности; способствовать возникновению интереса у большинства учеников; организовать досуг учащихся в свободное от учебы время.
• Только сбалансированное применение всех технологий позволит активизировать познавательный интерес учащихся, развивать их творческие способности

Древнекитайская мудрость.

• Отношение учащихся к тому или иному предмету определяется различными факторами: индивидуальными особенностями личности, особенностями самого предмета, методикой его преподавания.
• Одной из главных целей образования  является повышение педагогического мастерства преподавателя путём освоения современных технологий обучения и воспитания. В моём понимании технология – это символ упорядоченности, логичности, целенаправленности, ясности целей и средств – основа педагогических действий, направленных на всестороннее развитие личности учащегося.
• Применяя новые педагогические технологии на уроках, процесс обучения математики можно рассматривать с новой точки зрения и осваивать психологические механизмы формирования личности, добиваясь более качественных результатов. Особое значение математики в умственном воспитании и развитии отметил ещё в XVIII в. М. В. Ломоносов: «Математику уже затем учить следует, что она ум в порядок приводит».
•      Но сама по себе математика ум учащегося в порядок не приводит. Всё зависит от ориентации обучения, способа преподавания. И ни одна другая дисциплина не может конкурировать с возможностями математики в воспитании мыслящей личности.
• Увеличение умственной нагрузки на уроках математики заставляет меня задуматься над тем, как поддержать у учащихся интерес к изучаемому предмету. Ведь не секрет, что многие дети пасуют перед трудностями, а иногда и не хотят приложить определённых усилий для приобретения знаний. В своей практике я использую следующие современные образовательные технологии или их элементы:

Педагогические технологии и достигаемые результаты

• Дифференциация способствует более прочному и глубокому усвоению знаний, развитию индивидуальных способностей, развитию самостоятельного творческого мышления.
• Использование игровых технологий позволяет повысить эффективность учебного процесса, помогают достигать лучшего результата в обучении математике, повышают познавательный интерес к предмету.

Игровые технологии

• Отдельно остановимся на использовании игровых технологий.
• Я считаю, что использование на уроках игровых технологий обеспечивает достижение единства эмоционального и рационального в обучении. Так включение в урок игровых моментов делает процесс обучения более интересным, создает у учащихся хорошее настроение, облегчает преодоление трудности в обучении. Я использую их на разных этапах урока. Так в начале урока включаю игровой момент «Отгадай тему урока», при устном счете:
• - математический лабиринт,
• - магические квадраты,
• - элементы судоку,
• - кроссворды,
• - ребусы,
• - головоломки и др.
• При закреплении изученного материала – «Найди ошибку», кодированные упражнения. Так же мною разработаны викторины, часы занимательной математики, факультативы. Всё это направлено на расширение кругозора учащихся, развитие их познавательной деятельности, формирование определенных умений и навыков, необходимых в практической деятельности, развитие обще учебных умений и навыков. Игровые технологии находят также широкое применение во внеклассной работе.

Математические ребусы , кроссворды

• Задания 1 - 3. Решите числовые ребусы, где одинаковым буквам соответствуют одинаковые цифры, а разным - разные.

Математические ребусы , кроссворды

• Задание 4. Угадав все слова и записав их в клеточки по горизонтали, в выделенном вертикальном столбце вы прочтете фамилию известного ученого-математика Древней Греции.

. 3. Треугольник есть геометрическая ... . 4. Отрезок, соединяющий вершину треугольника 1 . Отрезок прямой, образующий прямой угол с данной прямой и имеющий одним из своих концов их точку пересечения, есть ... к данной прямой. 2. Элемент прямоугольного треугольника с серединой противоположной стороны.5. Два луча, исходящие из одной точки. 6. Перпендикуляр, опущенный из вершины конуса на плоскость основания. 7. Замкнутая плоская кривая, все точки которой находятся на одинаковом расстоянии от некоторой точки O.

Задание 5

Задание 5

• По горизонтали: 3. Отрезок прямой, соединяющий точку окружности с ее центром. 6. Утверждение, не требующее доказательства. 9. Конструкция, система мысли. 10. Вид четырехугольника. 15. Отрезок прямой, соединяющий две точки кривой. 16. Мера длины. 17. Тригонометрическая функция. 18. Точка пересечения диаметров окружности. 19. Тригонометрическая функция. 20. Часть окружности. 21. Старинная мера длины. По вертикали: 1. Символ какого-либо алфавита. 2. Вид параллелограмма. 4. Хорда, проходящая через центр окружности. 5.Геометрический элемент. 7. Луч, делящий угол пополам. 8. Символ греческого алфавита. 10. Сумма длин сторон треугольника. 11. Вспомогательное предложение, используемое для доказательства. 12. Элемент прямоугольного треугольника. 13. Одна из замечательных линий треугольника. 14. Тригонометрическая функция.

• Задание 7. По горизонтали: А. Половина числа A по вертикали, записанная от конца к началу. Г. Число, делящееся без остатка на 10 и на 17. Д. Разность наибольшего и наименьшего трехзначных чисел. По вертикали: А. Число, которое, будь оно на 400 больше, записывалось бы одинаковыми цифрами. Б. Число, третья цифра которого равна сумме двух первых цифр. В. Нечетное число.

• Задание 8. По горизонтали: А. Половина числа В по горизонтали. В. Число, все цифры которого одинаковы. Д. Квадрат числа Г по вертикали. Е. Число, две средние цифры которого одинаковы, последняя больше их, а первая цифра на 2 меньше любой из средних цифр. З. Квадрат целого числа. И. Сумма двух первых цифр числа Е по горизонтали. По вертикали: А. Число, которое на 2 меньше числа З по горизонтали. Б. Число, делящееся на 51. В. Квадрат целого числа. Г. Число, равное числу В по горизонтали. Е. Число, дающее при делении на 11 остаток, равный 10. Ж. Число, которое в 7 раз больше числа И по горизонтали.

Юный математик (5 класс)

• По горизонтали:   1.  Книга для занятий по какому-либо предмету.  4.  Перерыв в школьных занятиях.  6.  Знак, используемый для записи музыки . 9.  Документ, который выдают школьнику по окончании школы.  10.  Месяц.  11.  Большой лист, используемый для чертежей, стенгазет и т. п.  12. Чертежный инструмент.  13.  Предмет, используемый художником для нанесения краски на холст.
• По вертикали: 1.  Время, отведенное в школе для занятий одним из предметов . 2.  Знак, используемый для обозначения звука.  3.  Учреждение, которое дети посещают, пять раз в неделю.  5.  Деревянная палочка с грифелем.  7.  Жидкий состав для письма.  8.  Наука.
• Ответы:
• По горизонтали:  1. Учебник, 4. Каникулы, 6. Нота, 9. Аттестат. 10. Август. 11. Ватман. 12. Циркуль. 13. Кисть.
• По вертикали:  1. Урок. 2. Буква. 3. Школа. 5. Карандаш. 7. Чернила. 8. История.

Математик (6 класс)

• По горизонтали: 3.  Знаки, которые ставятся тогда, когда нужно изменить порядок действий.  4. Одна из точек, расположенных на координатном луче, имеющая большую координату.  8. Выдающийся советский математик, который в шестилетнем возрасте заметил, что 12 = 1, 22 = 1 + 3, 32 = 1 + 3 + 5, 42 = 1 + 3 + 5 + 7 и т. д.  9.  Числа, которые перемножают.  10.  Единица измерения отрезков учащимися в тетради.  13.  Основная единица массы.  14.  Неограниченная геометрическая фигура, которая не имеет краёв.
• По вертикали:   1.  Необходимая часть текста задачи.  2.  Единица измерения объёма жидкости, которая используется в Англии и США (4л. ).  5.  Прямоугольник, у которого все стороны равны.  6. Одно из измерений прямоугольного параллелепипеда . 7.  Число, которое иногда получается при делении.  11.  Число, которое делят.  12.  Отрезок, соединяющий вершины треугольника.
• Ответы:
• По горизонтали:  3. Скобки. 4. Правее. 8. Колмогоров. 9. Сомножители. 10. Сантиметр. 13. Килограмм. 14. Плоскость.
• По вертикали:  1. Вопрос. 2. Галлон. 5. Квадрат. 6. Длина. 7. Остаток. 11. Делимое. 12. Сторона.

Юный математик (5 класс)

• 1.  Буква латинского алфавита.  2.  Единица времени.  3.  Площадь квадрата со стороной 10 м.  4. Отрезок, соединяющий центр окружности с любой её точкой . 5.  Единица меры длины.  6.  Знак, употребляемый при сравнении чисел.  7.  Часть прямой, соединяющей две точки.  8.  Единица массы, равная 1000 г.  9.  Знак математического действия.  10.  Число, которое больше 36, но меньше 44.  11.  Прямоугольный параллелепипед, у которого все рёбра равны.  12.  Элементарный знак в какой-либо символике.  13.  Единица площади, применяемая во многих западных странах (» 4047 м2).  14.  Сторона грани куба.  15.  Число, которое иногда получается при делении.  16.  Группа цифр в записи числа.  17.  Знаки, которые ставятся тогда, когда нужно изменить обычный порядок действий.  18.  Буква латинского алфавита.  19.  Значение неизвестной буквы, при которой из уравнения получается числовое равенство.
• Ответы:
• 1. Икс.  2. Секунда.  3. Ар.  4. Радиус  5. Сантиметр.  6. Равно.7. Отрезок.  8. Килограмм.  9. Минус.  10. Сорок.  11. Куб.  12. Буква.13. Акр.  14. Ребро.  15. Остаток.  16. Класс.  17. Скобки. 1 18. Игрек.  19. Корень.

Любителям геометрии (7 класс )

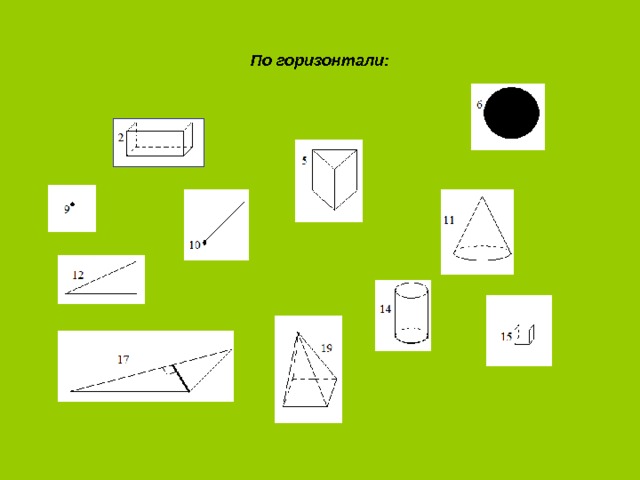
По горизонтали:

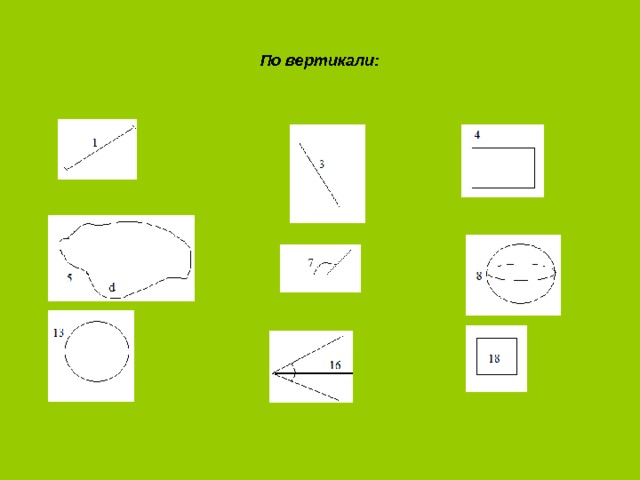
По вертикали:

Ответы:

• По горизонтали:  2. Параллелепипед. 5. Призма. 6. Круг. 9. Точка. 10. Луч. 11. Конус. 12. Треугольник. 14. Цилиндр. 15. Куб. 17. Высота. 19. Пирамида.
• По вертикали:  1. Отрезок. 3. Прямая. 4. Прямоугольник. 5. Плоскость. 7. Угол. 8. Шар. 13. Окружность. 16. Биссектриса. 18. Квадрат.

Юный математик (5 класс)

• 1.  Буква латинского алфавита.  2.  Единица времени.  3.  Площадь квадрата со стороной 10 м.  4. Отрезок, соединяющий центр окружности с любой её точкой . 5.  Единица меры длины.  6.  Знак, употребляемый при сравнении чисел.  7.  Часть прямой, соединяющей две точки.  8.  Единица массы, равная 1000 г.  9.  Знак математического действия.  10.  Число, которое больше 36, но меньше 44.  11.  Прямоугольный параллелепипед, у которого все рёбра равны.  12.  Элементарный знак в какой-либо символике.  13.  Единица площади, применяемая во многих западных странах (» 4047 м2).  14.  Сторона грани куба.  15.  Число, которое иногда получается при делении.  16.  Группа цифр в записи числа.  17.  Знаки, которые ставятся тогда, когда нужно изменить обычный порядок действий.  18.  Буква латинского алфавита.  19.  Значение неизвестной буквы, при которой из уравнения получается числовое равенство.
• Ответы:
• 1. Икс.  2. Секунда.  3. Ар.  4. Радиус  5. Сантиметр.  6. Равно.7. Отрезок.  8. Килограмм.  9. Минус.  10. Сорок.  11. Куб.  12. Буква.13. Акр.  14. Ребро.  15. Остаток.  16. Класс.  17. Скобки. 1 18. Игрек.  19. Корень.

Отгадай ребус

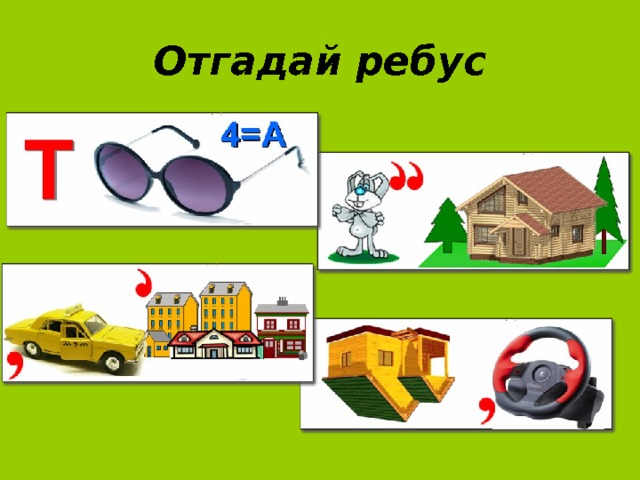
Отгадай ребус

Фрагменты уроков

Новый материал

Действия с одночленами

Устно

• Найди ошибки, исправь их и объясни
• Найди ошибки, исправь их и объясни
• Найди ошибки, исправь их и объясни
• Найди ошибки, исправь их и объясни
• Найди ошибки, исправь их и объясни

1) 5 • 5 • 5 •5 =4 5 ;

6) 2 3  + 2 7  = 2 10 ;

2) (–3) 2  = – 9;

7) 2 30  : 2 10  = 2 3 ;

3) 7 1 =1;

8) (2x) 3  = 2x 3 ;

4) 4 0  = 4;

9) (a 3 ) 2  = a 5 ;

5) 2 3 · 2 7  =2 21 ;

1 0) (–4) 2  = –16;

Самостоятельная работа

• Замените вопросительный знак и пробелы числами или буквами, чтобы получилось верное равенство:

а) 3,5 •2 ___ =7а;

б) -6х 3  • 9bх ?  = –54 bх 5 ;

в) -8а ? b 2 •8а 3 b ? =____а 5 b 7 ;

г) ( -7а ? b ? ) (4а 2 b)=-28а 4 b 4 ;

Здесь затеи и задачи,

Игры, шутки, все для вас!

Пожелаем вам удачи,

За работу, в добрый час!

финиш

финиш

Расставь на шарах цифры от 1 до 9 так , чтобы их суммы на каждой из сторон треугольника были равны.

Выясните, делится ли числовое

значение выражения

534 ∙974∙824 + 846∙916

на 10?

В этой зашифрованной записи одинаковые знаки обозначают одинаковые цифры от 0 до 9. Расшифруйте запись.

Какой фигуры нет на рисунке?

а) круга;

б) квадрата;

в) прямоугольника;

г) треугольника;

д) все перечисленные

фигуры есть.

Из четырех монет одна фальшивая, причем, неизвестно больше или меньше она по весу, чем настоящие монеты. За какое меньшее количество взвешиваний на рычажных весах можно определить эту монету?

A

B

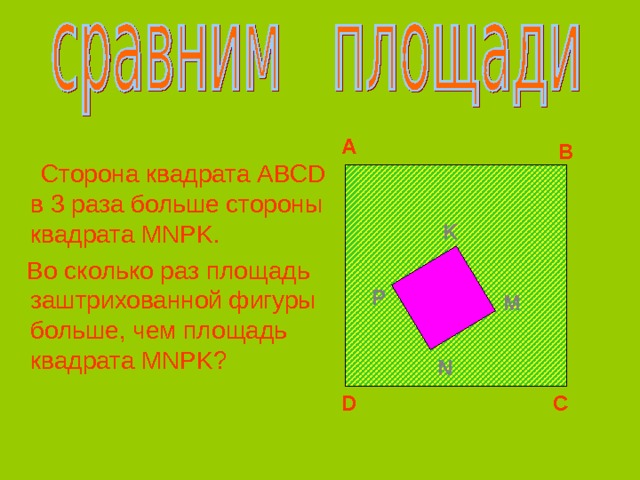
Сторона квадрата ABCD в 3 раза больше стороны квадрата MNPK .

Во сколько раз площадь заштрихованной фигуры больше, чем площадь квадрата MNPK ?

K

P

M

N

D

C

« О х , у ж э т а м а т е м а т и к а ! »

Здесь сидит желтый «Треугольник»

Будет рад им каждый школьник.

По плечу им все заданья,

Не страшны им состязанья!

«Треугольник»

За красным столиком налево

«Квадрат» сидит там смело.

Ему задачки не почем,

Смекалист, будет он во всем.

«Квадрат»

Вопросы команде «Квадрат»:

• Как называется дробь, числитель которой меньше знаменателя?
• Число 17 – простое или составное?
• Округлите 3,9 до единиц.
• Как называется число, изображенное на координатной прямой?
• Результат умножения?
• Расшифруйте НОК
• Единица с шестью нулями?
• Какое число не простое, ни составное?
• На сколько нужно умножить 2, чтобы получить 1?
• Как называются числа, используемые при счеты предметов?

Вопросы команде «Треугольник»

• Как называется дробь, числитель которой больше знаменателя?
• Число 9 простое или составное?
• Округлите 3,4 до единиц?
• Где на координатной прямой расположены точки с отрицательными координатами?
• Результат деления?
• Расшифруйте НОД
• Единица с четырьмя нулями?
• Самое маленькое натуральное число?
• Назовите число обратное 3?
• Что такое периметр?

«Шифровальщик»

«Шифровальщик»

«Снайпер».

«Угадай слово».

• За это снижают оценку.
• Отличники их не делают.
• На них учатся.

• 3апомнить их не возможно.
• По ним считают.
• Их полно в справочнике

• В стране они нас пугают.
• Самое приятное в школе.
• Между уроками.

• Как муравьев в муравейнике...
• Бывает пустое.
• Состоит из элементов.

• Решение уравнения.
• У некоторых овощей только он и есть.
• Его обычно извлекают
• У каждой задачи он должен быть.
• Можно честно его искать, а можно и подогнать или подсмотреть.
• А она говорит “Провинился, – изволь держать ...”

• Под ней звенят бубенчики.
• У стрелкового лука.
• Кусок окружности
• Обычно находится в центре города.
• Выражается квадратным числом.
• Длина на ширину.

МАТЕМАТИКА

Ах, эта математика – Наука очень строгая. Учебник математики Всегда берешь с тревогою. Там функции и графики И уравнений тьма, А модуль может запросто Свести тебя с ума. И правила, и формулы, Все так легко забыть, Но все ж без математики Нам невозможно жить. Любите математику И вы поймете вдруг, Что, правда: “Математика – Царица всех наук!”