ПРОИЗВОДНАЯ ФУНКЦИИ.
(Раздел «Начала математического анализа»)
ДЕЯТЕЛЬНОСТНАЯ КАРТА УЧЕБНОГО ЗАНЯТИЯ
Профессии: 15.01.20 Слесарь по контрольно-измерительным приборам и автоматике, 09.01.03 Мастер по обработке цифровой информации, 23.01.03 Автомеханик, 09.01.01 Наладчик аппаратного и программного обеспечения
Учебные группы: КИП-11, М-11, А-11, Н-11
Учебная дисциплина: ООПу.04 Математика
Тема учебного занятия: Производная функции.
Тип урока: урок «открытия» новых знаний
Вид урока: лекция-беседа
Средства обучения:
технические: мультимедийный проектор, персональный компьютер;
информационно-коммуникационные: электронная презентация.
Цели урока:
методическая: использование объяснительно-иллюстративного метода обучения с целью формирования математического мышления студентов;
образовательная: создание условий для овладения знаниями о последовательностях и пределах последовательностей;
развивающая: развитие умений планировать, анализировать, выдвигать гипотезы по решению заданий, применять полученные знания для выполнения упражнений;
воспитательная: воспитание интереса к изучению математики, математической культуры студентов.
Прогнозируемые результаты:
1) предметные:
сформированность знаний о производной функции;
владение умением решать задачи на производные функции;
2) метапредметные:
умение ставить перед собой цель, видеть ожидаемый результат работы;
умение рационально распределять рабочее время;
умение объективно оценивать свои возможности, анализировать свои результаты, корректировать свои действия;
владение навыками познавательной рефлексии;
умение осуществлять поиск и отбор необходимой информации;
умение сопоставлять и анализировать, выделять в тексте базовые и вспомогательные концепты, опорные понятия, тезисы, структурировать их взаимосвязь;
умение структурировать полученную информацию;
умение анализировать и обобщать информацию;
умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности;
умение выражать свои мысли с достаточной полнотой и точностью.
Образовательные технологии: традиционное обучение.
Формы организации обучения: фронтальная, индивидуальная.
Методы обучения и контроля:
вербальные: беседа;
практические: метод сравнения, метод анализа и структурирования.
методы контроля и самоконтроля: устный контроль, самоконтроль.
Нормативный документ
Федеральный государственный образовательный стандарт среднего общего образования (утв. приказом Министерства образования и науки Российской Федерации (Минобрнауки России) от 17 мая 2012 г. № 413 г.). – М.: Министерство образования и науки РФ, – 2012.
Образовательные ресурсы:
Основная литература
Башмаков М. И. Математика: учебник для студ. учреждений сред. проф. образования. − М.: Издательский центр «Академия», 2018. – 256 с.
Башмаков М. И. Математика. Сборник задач профильной направленности: учеб. пособие для студ. учреждений сред. проф. образования. − М.: Издательский центр «Академия», 2014. – 416 с.
Дополнительная литература
Алимов Ш.А., Колягин Ю.М. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. Учебник. − М.: Просвещение, 2014. – 464 с.
Атанасян Л.С. Геометрия. 10 − 11 классы: учебник для общеобразовательных учреждений: базовый и профильный уровни / Атанасян Л.С., Бутузов В.Ф. и др. – М.: Просвещение, 2013. – 255 с.
Богомолов Н.В. Практические занятия по математике: Учеб. пособие для техникумов / Н.В. Богомолов. – М.: Высш. шк., 2013. – 495 с.
Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (Книга 1): Учебное пособие. – М.: Издательство «Новая волна», 2013. – 656 с.
Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (Книга 2): Учебное пособие. – М.: Издательство «Новая волна», 2013. – 592 с.
Никольский С.М. Алгебра и начала анализа: учебник для 10 класса общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов. – М.: Просвещение, 2013. – 430 с.
Никольский С.М. Алгебра и начала анализа: учебник для 11 класса общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов. – М.: Просвещение, 2013. – 464 с.
Интернет-ресурсы:
Федеральный центр информационно-образовательных ресурсов [Электронный ресурс] URL: www. fcior. edu. ru
Единая коллекции цифровых образовательных ресурсов [Электронный ресурс] URL: www. school-collection. edu. ru
Научно-методические ресурсы:
Инновационные педагогические технологии: учебное пособие/ Михелькевич В.Н., Нестеренко В.М., Кравцова П.Г. – Самар. гос. тех. ун-т Самара, 2001. – 89 с.
Кульневич С.В., Лакоценина Т.П. Современный урок. Часть 1: Научно-практич. пособие для учителей, методистов, руководителей учебных заведений, студентов пед. заведений, слушателей ИПК. – Ростов н/Д: Учитель, 2005. – 288 с.
Кульневич С.В., Лакоценина Т.П. Современный урок. Часть 3: Научно-практич. пособие для учителей, методистов, руководителей учебных заведений, студентов пед. заведений, слушателей ИПК. – Ростов н/Д: Учитель, 2007. – 288 с.
Махмутов М.И. Проблемное обучение: Основные вопросы теории. – М.: Педагогика, 1975. – 368 с.
Основные термины и понятия: производная функции.
ПЛАН УЧЕБНОГО ЗАНЯТИЯ
Содержание учебного материала:
1) Сформированность знаний о вычислениях производной функции.
2) Закрепление теоретического материала по теме с помощью решения упражнений.
Этап мотивации (самоопределения) к учебной деятельности (2 мин)
Преподаватель приветствует студентов, создает деловую обстановку, настраивает на продуктивную мыслительную деятельность.
Этап актуализации опорных знаний. Целеполагание (15 мин)
Преподаватель задает вопросы студентам:
Какие вы знаете производные функции?
Приведите пример производной функции.
Студенты отвечают на эти вопросы, вспоминая знания, полученные на предыдущем занятии.
Формулирование темы и целей учебного занятия.
Работа над новой темой («открытие» нового знания) (48 мин)
Алгоритм работы над «открытием» нового знания:
Формулирование преподавателем определения производной функции.
Предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю (и этот предел существует), называется производной этой функции.
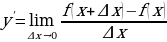 .
.
(Часто вместо 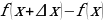 пишется
пишется 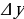 .)
.)
Итак, 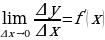 .
.
Иногда используются обозначения 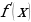 или
или 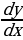 .
.
Пример:
1) 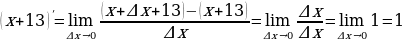 ;
;
2) 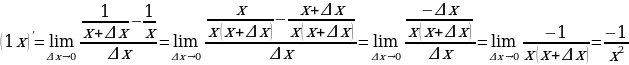 .
.
Задача 1 (о скорости движения). По прямой, на которой заданы начало отсчёта, единица измерения (метр) и направление, движется некоторое тело (материальная точка). Закон движения задан формулой 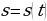 , где
, где 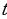 — время (в секундах),
— время (в секундах), 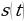 — положение тела на прямой (координата движущейся материальной точки) в момент времени
— положение тела на прямой (координата движущейся материальной точки) в момент времени 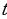 по отношению к началу отсчёта (в метрах). Найти скорость движения тела в момент времени
по отношению к началу отсчёта (в метрах). Найти скорость движения тела в момент времени 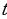 (в м/с).
(в м/с).
Решение. Предположим, что в момент времени 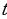 тело находилось в точке
тело находилось в точке 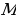 .
.
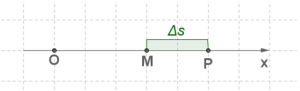
Дадим аргументу 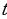 приращение
приращение 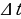 и рассмотрим ситуацию в момент времени
и рассмотрим ситуацию в момент времени 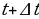 . Координата материальной точки станет другой, тело в этот момент будет находиться в точке
. Координата материальной точки станет другой, тело в этот момент будет находиться в точке 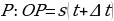 .
.
Значит, за 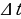 секунд тело переместилось из точки
секунд тело переместилось из точки 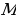 в точку
в точку 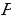 . Имеем:
. Имеем: 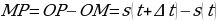 . Полученную разность мы назвали приращением функции:
. Полученную разность мы назвали приращением функции: 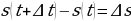 . Итак,
. Итак, 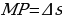 (м). Нетрудно найти среднюю скорость 𝑣ср движения тела за промежуток времени
(м). Нетрудно найти среднюю скорость 𝑣ср движения тела за промежуток времени 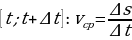 (м/с).
(м/с).
А что такое скорость 𝑣(𝑡) в момент времени 𝑡 (её называют мгновенной скоростью)? Можно сказать так: это средняя скорость движения за промежуток времени 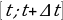 при условии, что
при условии, что 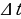 выбирается всё меньше и меньше; точнее: при условии, что
выбирается всё меньше и меньше; точнее: при условии, что 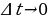 . Это значит, что
. Это значит, что 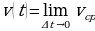 .
.
Итак,
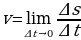 .
.
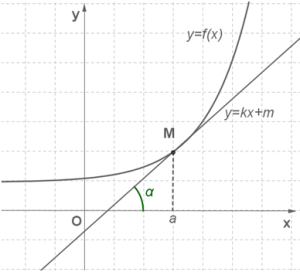
Задача 2 (о касательной к графику функции). Дан график функции 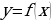 . На нём выбрана точка
. На нём выбрана точка 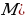 ), в этой точке к графику функции проведена касательная (мы предполагаем, что она существует). Найти угловой коэффициент касательной.
), в этой точке к графику функции проведена касательная (мы предполагаем, что она существует). Найти угловой коэффициент касательной.
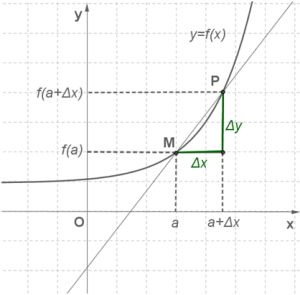
Решение. Дадим аргументу приращение 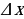 и рассмотрим на графике точку
и рассмотрим на графике точку 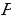 с абсциссой
с абсциссой 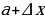 . Ордината точки
. Ордината точки 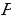 равна
равна 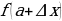 . Угловой коэффициент секущей
. Угловой коэффициент секущей 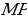 , т. е. тангенс угла между секущей и осью
, т. е. тангенс угла между секущей и осью 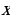 , вычисляется по формуле
, вычисляется по формуле 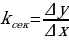 .
.
Если мы теперь устремим 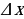 к нулю, то точка
к нулю, то точка 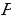 начнёт приближаться по кривой к точке
начнёт приближаться по кривой к точке 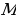 . Касательную мы охарактеризовали как предельное положение секущей при этом приближении. Значит, естественно считать, что угловой коэффициент касательной
. Касательную мы охарактеризовали как предельное положение секущей при этом приближении. Значит, естественно считать, что угловой коэффициент касательной 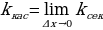 будет вычисляться по формуле
будет вычисляться по формуле 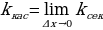 . Используя приведённую выше формулу для
. Используя приведённую выше формулу для 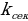 , получаем:
, получаем:
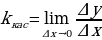 .
.
Включение нового знания в систему имеющихся знаний (20 мин)
Примеры
Физический (механический) смысл производной состоит в следующем. Если 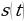 — закон прямолинейного движения тела, то производная выражает мгновенную скорость в момент времени
— закон прямолинейного движения тела, то производная выражает мгновенную скорость в момент времени 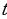 :
:
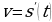 .
.
Геометрический смысл производной состоит в следующем. Если к графику функции 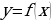 в точке с абсциссой
в точке с абсциссой 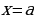 можно провести касательную, не параллельную оси
можно провести касательную, не параллельную оси 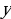 , то
, то 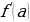 выражает угловой коэффициент касательной:
выражает угловой коэффициент касательной:
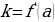 .
.
Поскольку 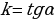 , то верно равенство
, то верно равенство 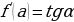 .
.
Алгоритм нахождения производной для функции 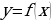
1. Зафиксировать значение 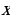 , найти
, найти 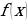 .
.
2. Дать аргументу 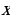 приращение
приращение 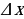 , перейти в новую точку
, перейти в новую точку 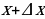 , найти
, найти 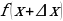 .
.
3. Найти приращение функции: 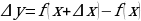 .
.
4. Составить отношение 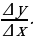
5. Вычислить  . Этот предел и есть
. Этот предел и есть 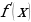 .
.
Рефлексия. Подведение итогов учебного занятия (5 мин)
Беседа со студентами по содержанию занятия. Вопросы для беседы:
Какая была тема сегодняшнего занятия?
Что нового вы узнали?
Какая была цель занятия?
Что получилось у вас сегодня?
Что не получилось?
Достигли ли мы поставленной цели?
Инструктирование о выполнении домашнего задания
Изучить [1] гл. 9 занятие 3-5







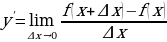 .
.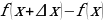 пишется
пишется 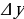 .)
.)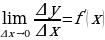 .
.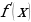 или
или 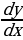 .
.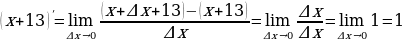 ;
; .
.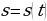 , где
, где 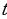 — время (в секундах),
— время (в секундах), 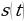 — положение тела на прямой (координата движущейся материальной точки) в момент времени
— положение тела на прямой (координата движущейся материальной точки) в момент времени 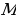 .
.
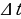 и рассмотрим ситуацию в момент времени
и рассмотрим ситуацию в момент времени 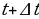 . Координата материальной точки станет другой, тело в этот момент будет находиться в точке
. Координата материальной точки станет другой, тело в этот момент будет находиться в точке 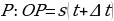 .
.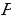 . Имеем:
. Имеем: 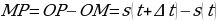 . Полученную разность мы назвали приращением функции:
. Полученную разность мы назвали приращением функции: 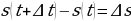 . Итак,
. Итак, 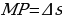 (м). Нетрудно найти среднюю скорость 𝑣ср движения тела за промежуток времени
(м). Нетрудно найти среднюю скорость 𝑣ср движения тела за промежуток времени 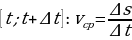 (м/с).
(м/с).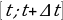 при условии, что
при условии, что 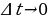 . Это значит, что
. Это значит, что 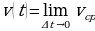 .
.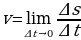 .
.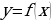 . На нём выбрана точка
. На нём выбрана точка 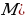 ), в этой точке к графику функции проведена касательная (мы предполагаем, что она существует). Найти угловой коэффициент касательной.
), в этой точке к графику функции проведена касательная (мы предполагаем, что она существует). Найти угловой коэффициент касательной.
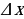 и рассмотрим на графике точку
и рассмотрим на графике точку 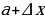 . Ордината точки
. Ордината точки 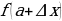 . Угловой коэффициент секущей
. Угловой коэффициент секущей 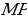 , т. е. тангенс угла между секущей и осью
, т. е. тангенс угла между секущей и осью 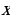 , вычисляется по формуле
, вычисляется по формуле 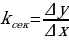 .
.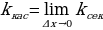 будет вычисляться по формуле
будет вычисляться по формуле 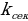 , получаем:
, получаем: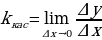 .
.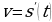 .
.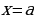 можно провести касательную, не параллельную оси
можно провести касательную, не параллельную оси 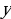 , то
, то 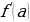 выражает угловой коэффициент касательной:
выражает угловой коэффициент касательной: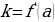 .
.
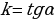 , то верно равенство
, то верно равенство 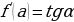 .
.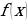 .
.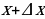 , найти
, найти 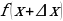 .
.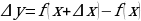 .
.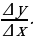
 . Этот предел и есть
. Этот предел и есть 









