Решение упражнений по теме: Уравнение касательной к графику функции.
Цели урока: повторить правила дифференцирования функций, уравнение касательной к графику функции в заданной точке, геометрически и физический смысл производной. Отработать навык составления уравнения касательной к графику функции в заданной точке, находить тангенс угла наклона касательной и ее угловой коэффициент.
Ход урока.
1. Организационный момент.
2. Устная работа.
По готовому рисунку ответить на вопросы.
Вариант 1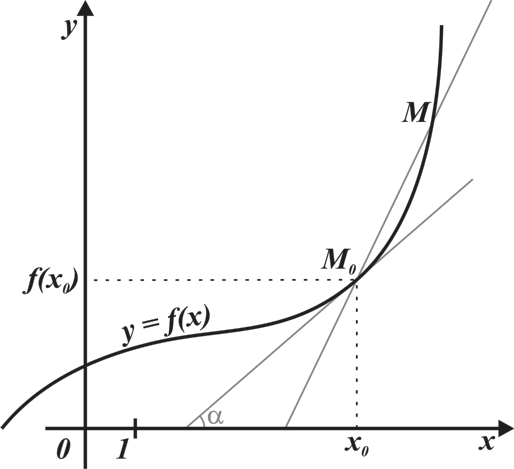
Что называется секущей для графика функции?
Чему равен угол наклона касательной к графику функции в заданной точке?
Как определяется тангенс угла наклона касательной?
Известно, что угловой коэффициент касательной к графику функции в точке с абсциссой 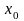 равен 0,5. Чему равно значение производной в этой точке?
равен 0,5. Чему равно значение производной в этой точке?
В чем заключается геометрический смысл производной?
Записать уравнение касательной к графику функции в заданной точке в общем виде.
Вариант 2
Какая прямая называется касательной к графику функции?
Какая из отмеченных точек является точкой касания? Определите ее координаты.
Как находится угловой коэффициент касательной?
Касательная к графику функции f(x) в точке с абсциссой образует с положительным направлением оси OX угол 30 градусов. Найдите в этой точке.
Алгоритм составления уравнения касательной к графику функции f(x) в точке.
В чем заключается физический смысл производной?
3. Решение задач.
Разобрать следующие задачи.
А)Найдите скорость изменения функции 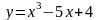 в точке
в точке 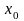 =2
=2 .
.
Б)Найдите ускорение функции 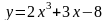 в точке
в точке 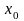 =1
=1
Составить уравнение касательной к графику заданной функции в точке с абсциссой 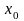 :
:
а) 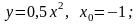
б) 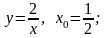
в) 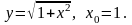
Найдите угловой коэффициент касательной, проведенной к графику функции 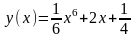 через точку с абсциссой x = 1.
через точку с абсциссой x = 1.
В каких точках касательные к графику функции 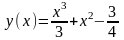 параллельны оси OX.
параллельны оси OX.
4. Самостоятельная работа (с выбором ответа)
Вариант 1
1. Найдите тангенс угла наклона касательной, проведенной к графику функции 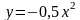 в его точке с абсциссой
в его точке с абсциссой 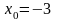 .
.
1) -3; 2) -4,5; 3) 3; 4) 0.
2. Найдите угловой коэффициент касательной, проведенной к графику функции 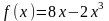 в его точке с абсциссой
в его точке с абсциссой 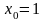 .
.
1) -3; 2) 0; 3) 2; 4) 5
3. К графику функции 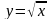 проведена касательная в точке с абсциссой
проведена касательная в точке с абсциссой 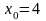 . Как расположена точка пересечения этой касательной с осью OY.
. Как расположена точка пересечения этой касательной с осью OY.
1) выше точки (0; 0); 2) ниже точки (0; 0);
3) выше точки (0; 1); 4) в точке (0; 0).
Вариант 2
1. Найдите угловой коэффициент касательной, проведенной к графику функции 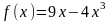 в его точке с абсциссой
в его точке с абсциссой 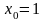 .
.
1) -3; 2) 0; 3) 3; 4) 5.
Решение:
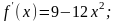
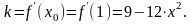
Ответ: 1.
2. Найдите тангенс угла наклона касательной, проведенной к графику функции 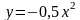 в его точке с абсциссой
в его точке с абсциссой 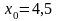 .
.
1) -3; 2) -4,5; 3) 3; 4) 0.
3. К графику функции 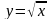 проведена касательная в точке с абсциссой
проведена касательная в точке с абсциссой 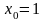 . Как расположена точка пересечения этой касательной с осью OY.
. Как расположена точка пересечения этой касательной с осью OY.
1) выше точки (0; 0); 2) ниже точки (0; 0);
3) выше точки (0; 1); 4) в точке (0; 0).
|
| Вариант 1 | Вариант 2 |
| 1 | 3 | 1 |
| 2 | 3 | 2 |
|
| 1 | 1 |
5. Итоги урока.
6. Домашнее задание.
Знать уравнение касательной к графику функции в данной точке.
Решить следующие задачи.
1. Найдите тангенс угла наклона касательной, проведенной к графику функции  в точке с абсциссой
в точке с абсциссой  .
.
2. Найдите угловой коэффициент касательной, проведенной к графику функции в его точке с абсциссой  .
.
3. Определите абсциссы точек, в которых угловой коэффициент касательной к графику функции  равен 1.
равен 1.







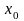 равен 0,5. Чему равно значение производной в этой точке?
равен 0,5. Чему равно значение производной в этой точке?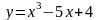 в точке
в точке  .
.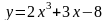 в точке
в точке 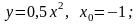
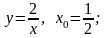
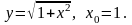
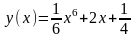 через точку с абсциссой x = 1.
через точку с абсциссой x = 1.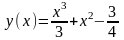 параллельны оси OX.
параллельны оси OX.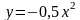 в его точке с абсциссой
в его точке с абсциссой 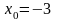 .
.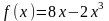 в его точке с абсциссой
в его точке с абсциссой 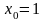 .
.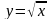 проведена касательная в точке с абсциссой
проведена касательная в точке с абсциссой 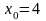 . Как расположена точка пересечения этой касательной с осью OY.
. Как расположена точка пересечения этой касательной с осью OY.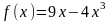 в его точке с абсциссой
в его точке с абсциссой 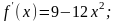
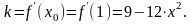
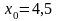 .
.









