Симметрия вокруг нас

Муниципальное казённое общеобразовательное учреждение «Средняя общеобразовательная школа №1 ст. Кардоникской»

Исследовательская работа по теме:

Авторы: Чотчаева Н

МКОУ «СОШ №1 ст. Кардоникской №1»

Руководитель: Тоценко Т.В.

учитель математики

МКОУ «СОШ №1 ст. Кардоникской №1»

Тема исследования: Симметрия в современном мире
Проблемные  вопросы:
- Что такое симметрия? 
- Где встречается симметрия?
- В каких областях жизни человека применяется симметрия?
Постановка проблемы: Выявить в каких областях встречается симметрия.
Гипотеза исследования: Симметрия встречается везде
Цели исследования: Выяснить, что такое симметрия и где ее можно встретить
Задачи исследования:
- Рассмотреть виды симметрии
- Найти симметричные объекты в окружающем мире
- Определить значение использования симметрии

СОДЕРЖАНИЕ.

Введение.

Глава 1. Виды симметрии …………………………………………………………. Стр.3-5

1. Определение симметрии

1.2Центральная симметрия

1.3Осевая симметрия.

1.4Зеркальная симметрия.

Глава 2. Симметрия в природе……………………………………………………….Стр.6-8

Глава 3. Симметрия в человеке………………………………………………………..Стр. 9-10

Глава 4. Симметрия в архитектуре………………………………………………… Стр.11-14

Глава 5. Использование симметрии в декоративно-прикладном искусстве……….Стр.15-23

Заключение.

Список литературы.

ВВЕДЕНИЕ.

О, симметрия! Гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты в Эйфелевой башне, в малой мошке,
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!

Симметрия является фундаментальным свойством природы, представление о котором, как отмечал академик В. И. Вернадский (1863—1945), «слагалось в течение десятков, сотен, тысяч поколений". «Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло ее в рисунке и в предметах быта». «Принцип симметрии в XX веке охватывает все новые области. Из области кристаллографии, физики твердого тела он вошел в область химии, в область молекулярных процессов и в физику атома. Нет сомнения, что его проявления мы найдем в еще более далеком от окружающих нас комплексов мире электрона и ему подчинены будут явления квантов».
Этими словами академика В. И. Вернадского и хочется начать короткий разговор о принципах симметрии в неживой природе.

ЗАГЛЯНЕМ В СЛОВАРЬ

Если мы возьмем на себя труд заглянуть в «Современный словарь иностранных слов», то обнаружим, что под симметрией понимается «соразмерность, полное соответствие в расположении частей целого относительно средней линии, центра... такое расположение точек относительно точки (центра симметрии), прямой (оси симметрии) или плоскости (плоскости симметрии), при котором каждые две соответствующие точки, лежащие на одной прямой, проходящей через центр симметрии, на одном перпендикуляре к оси или плоскости симметрии, находятся от них на одинаковом расстоянии...»
И это еще не все, как часто бывает с иностранными словами, значений у слова «симметрия» существует множество. В том-то и состоит преимущество подобных выражений, что их можно использовать в случае, когда не хотят дать однозначное определение или просто не знают четкого различия между двумя предметами.
Термин «соразмерный» мы применяем по отношению к человеку, картине или какому-либо предмету, когда мелкие несоответствия не позволяют употребить слово «симметричный».
Давайте также заглянем в Энциклопедический словарь. Мы обнаружим здесь шесть статей, начинающихся со слова «симметрия». Кроме того, это слово встречается во множестве других статей.
В математике слово «симметрия» имеет не меньше семи значений (среди них симметричные полиномы, симметрические матрицы). В логике существуют симметричные отношения. Важную роль играет симметрия в кристаллографии. Интересно интерпретируется понятие симметрии в биологии. Там описывается шесть различных видов симметрии. Мы узнаем, например, что гребневики дисимметричны, а цветки львиного зева отличаются билатеральной симметрией. Мы обнаружили, что симметрия существует в музыке и хореографии (в танце). Она зависит здесь от чередования тактов. Оказывается, многие народные песни и танцы построены симметрично.

В древности слово «СИММЕТРИЯ» употреблялось в значении «гармония», «красота». Действительно, в переводе с греческого это слово обозначает «соразмерность, пропорциональность, одинаковость в расположении частей.

Симметрия постоянно встречается в нашей жизни. Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Симметрия широко распространена в природе, искусстве и архитектуре.

Симметрия в природе – это проявление стремления материи к надёжности и прочности. Симметрия проявляется в строении организмов многих живых существ: человек, бабочка, морская звезда, листья и цветы многих растений. Симметрию можно увидеть в строении снежинок и различных кристаллов.

В искусстве симметрия получила распространение как один из видов гармоничной композиции. Она свойственна произведениям архитектуры (являясь непременным качеством если не всего сооружения в целом, то его частей и деталей - плана, фасада, колонн, капителей и т. д.) и декоративно-прикладного искусства.  Центральная и осевая симметрии в сочетании с поворотами и переносами являются основными приёмами построения орнаментов.

Cуществует несколько видов симметрии. В школьном курсе геометрии рассматриваются только два вида симметрии – осевая и центральная.

Глава 1. Виды симметрии.

1.1. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ 

 

 

Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1. Точка О считается симметричной самой себе, она является центром симметрии.

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметрична ей точка относительно точки О также принадлежит этой фигуре.

 

 

 

 

 

 

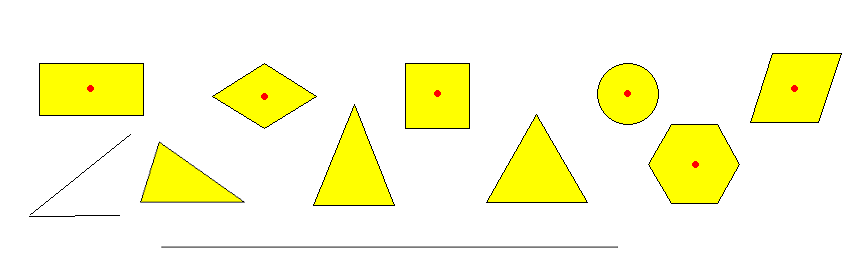
 Представление о центральной симметрии нам дают следующие иллюстрации. (Приложение 1 ) 

Фигуры, обладающие центральной симметрией – окружность, параллелограмм, ромб, квадрат, прямоугольник, правильный шестиугольник. Они имеют по одному центру симметрии. Прямая также обладает центром симметрии, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии, у прямой их бесконечное множество – любая точка прямой является центром симметрии. Фигуры, не имеющие центра симметрии – все треугольники, угол.

 

 

 

 

 

 

 

 

 

 

1.2 ОСЕВАЯ СИММЕТРИЯ

 

Две точки А и А₁ называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА₁ и перпендикулярна к нему. Каждая точка прямой а симметрична сама себе.

 

 

 

 

 

 

 

 

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии. Говорят также, что фигура обладает осью симметрии.

У развёрнутого угла есть своя ось симметрии – прямая, на которой расположена биссектриса угла. Равнобедренный (но не равносторонний) треугольник имеет также одну ось симметрии, а равносторонний – три оси симметрии. Прямоугольник и ромб, не являющиеся квадратами имеют по две оси симметрии, квадрат – четыре оси симметрии, а правильный шестиугольник – шесть осей симметрии. У окружности их бесконечное множество – любая прямая, проходящая через её центр, является осью симметрии. Имеются две фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.

1.3 ЗЕРКАЛЬНАЯ СИММЕТРИЯ.

 

 

  Что может быть больше похоже на мою руку

или мое ухо, чем их собственное отражение в зеркале?

И все же руку которую я вижу в зеркале,

нельзя поставить на место настоящей руки.

                Иммануил Кант.

Достаточно взглянуть на окружающий нас реальный мир, чтобы убедиться в первостепенном значении зеркальной симметрии с соответствующим симметричным элементом – плоскостью симметрии. В самом деле, форма всех объектов, которые двигаются по земной поверхности или возле нее – шагают, плывут, летят, катятся, - обладает, как правило, одной более или менее хорошо выраженной плоскостью симметрии.

    Обычно считают, что наблюдаемый в зеркале двойник является точной копией самого объекта. В действительности это не совсем так. Зеркало не просто копирует объект, а меняет местами (переставляет) передние и задние по отношению к зеркалу части объекта. В сравнении с самим объектом его зеркальный двойник оказывается "вывернутым" вдоль направления перпендикулярного к плоскости зеркала.

Предположим, что одна половина объекта является зеркальным двойником по отношению к другой его половине. Такой объект называют зеркально симметричным. Он преобразуется сам в себя при отражении в соответствующей зеркальной плоскости . Эту плоскость называют плоскостью симметрии .

  Напишем на листе бумаги заглавными печатными буквами два слова "КОФЕ" и "ЧАЙ". Затем возьмем зеркало и поставим его вертикально так , чтобы линия пересечения плоскости зеркала с плоскостью листа делила эти слова по горизонтали .

Зеркало не подействовало на слово " КОФЕ ", тогда как слово " ЧАЙ " оно изменило до неузнаваемости. Этот " фокус " имеет простое объяснение . Разумеется , зеркало одинакововым образом отражает нижнюю половину обеих слов . Однако в отличие от слова " ЧАЙ " слово " КОФЕ " обладает горизонтальной осью симметрии , именно поэтому оно не искажается при отражении в зеркале .

Глава 2.

Симметрия в природе

Математика…
выявляет порядок, симметрию и определенность,
а это – важнейшие виды прекрасного.

Аристотель

Трудно найти человека, который не имел бы какого-то представления о симметрии. “Симметрия” - слово греческого происхождения. Оно, как и слово “гармония”, означает соразмерность, наличие определенного порядка, закономерности в расположении частей. Известный немецкий математик Герман Вейль дал определение симметрии таким образом: “Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство”

Природа – удивительный творец и мастер. Все живое в природе обладает свойством симметрии.

Если сверху посмотреть на любое насекомое и мысленно провести посередине прямую (плоскость), то левые и правые половинки насекомых будут одинаковыми и по расположению, и по размерам, и по окраске. Ведь мы ни разу не видели, чтобы у жука или стрекозы, у любого другого насекомого лапы слева были бы ближе к голове, чем справа, а правое крыло бабочки или божьей коровки было бы больше, чем левое. Такого в природе не бывает, иначе бы насекомые не смогли бы летать.

Представление об осевой симметрии нам дают следующие иллюстрации. (Приложение 1)

Симметрична бабочка. Форма и окраска правого крыла повторяют очертания и рисунок левого. Когда бабочка сложит крылья, эти рисунки совмещаются.

Симметрию можно увидеть среди цветов. Осевой симметрией обладают цветки семейства розоцветных, а центральной симметрией – семейство крестоцветных. Симметрию можно увидеть и на листьях деревьев.

Однако симметрия существует и там, где ее не видно на первый взгляд. В мир неживой природы очарование симметрии вносят кристаллы. Физик скажет, что всякое твердое тело – кристалл. Знаменитый кристаллограф Евграф Степанович Федоров сказал: “Кристаллы блещут симметрией”. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией. (Приложение 2)

У шестиугольной снежинки вы легко обнаружите шесть плоскостей симметрии. Сгибая рисунок по любой из линий, изображающих следы плоскости симметрии снежинки, вы совместите друг с другом две половины её.

Ось симметрии имеет то свойство, что при повороте вокруг нее на некоторый определенный угол соответствующие части фигуры совмещаются друг с другом. Смотря по тому, на какой угол приходится повернуть при этом тело, различают у кристаллов оси 2,3,4,6-го порядка. Например, у снежинок имеется одна ось 6-го порядка (перпендикулярная к плоскости чертежа). Центром симметрии называется точка внутри тела, на равном расстоянии от которой в диаметрально противоположных направлениях расположены одинаковые элементы тела.
А что такое кристалл? Твердое тело, имеющие естественную форму многогранника. Характерная особенность того или иного вещества состоит в постоянстве углов между соответственными гранями и ребрами для всех образов кристаллов одного и того же вещества.
Что же касается формы граней ,числа граней и ребер и величины кристалла, то для одного и того же вещества они могут значительно отличаться друг от друга.
Для каждого данного вещества существует своя, присущая только ему идеальная форма его кристалла. Эта форма обладает свойством симметрии т.е. свойством кристаллов совмещаться с собой в различных положениях путём поворотов, отражений, параллельных переносов. Среди элементов симметрии различаются оси симметрии, плоскости симметрии, центр симметрии, зеркальные оси.

Показанный на рисунке кристалл при повороте на1/4 окружности вокруг оси АВ совмещается сам с собой. Значит, мы имеем ось 4-го порядка. Тот же кристалл совмещается сам с собой при отражении в плоскости СDEF ( как если бы это была плоскость зеркала); это есть плоскость симметрии.
Химик скажет, что все тела состоят из молекул, а молекулы состоят из атомов. А многие атомы располагаются в пространстве по принципу симметрии. Внутреннее устройство кристалла представляется в виде пространственной решётки, в одинаковых ячейках которой, имеющих форму параллелепипедов, размещены по законам симметрии одинаковые мельчайшие частицы - молекулы, атомы, ионы и их группы. Многие, если не все, кристаллы более или менее легко раскалываются по некоторым строго определённым плоскостям. Это явление называется спайностью и свидетельствует о том, что механические свойства кристаллов анизотропны т. е. не одинаковы по разным направлениям.
Симметрия внешней формы кристалла является следствием его внутренней симметрии - упорядоченного взаимного расположения в пространстве атомов ( молекул).

Таким образом, данное преобразование фигур (симметрия) вошло в математику в результате наблюдения человека за окружающим миром. Оно встречается часто и повсеместно. Поэтому даже не искушенный человек обычно легко усматривает симметрию в относительно простых ее проявлениях.

Свойство симметричности, присущее живой природе, человек использовал в своих достижениях:: изобрел самолет, создал уникальные здания архитектуры. (Приложение 3)

Да и сам человек является фигурой симметричной.

Глава 3.

Симметрия в человеке.

Не станем пока разбираться, существует ли на самом деле абсолютно симметричный человек. У каждого, разумеется, обнаружится родинка, прядь волос или какая-нибудь другая деталь, нарушающая внешнюю симметрию. Левый глаз никогда не бывает в точности таким, как правый, да и уголки рта находятся на разной высоте, во всяком случае у большинства людей.

И все же это лишь мелкие несоответствия. Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы!

НО! Здесь стоит остановиться. Если бы наши руки и в самом деле были совершенно одинаковы, мы могли бы в любой момент поменять их. Было бы возможно, скажем, путем трансплантации пересадить левую ладонь на правую руку, или, проще, левая перчатка подходила бы тогда к правой руке, но на самом деле это не так.

Каждому известно, что сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале. Именно вопросам симметрии и зеркального отражения здесь и уделяется внимание.

Многие художники обращали пристальное внимание на симметрию и пропорции человеческого тела, во всяком случае до тех пор, пока ими руководило желание в своих произведениях как можно точнее следовать природе. Известны каноны пропорций, составленные Альбрехтом Дюрером и Леонардо да Винчи. Согласно этим канонам, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат. Дюрер занимался поисками единой меры, которая находилась бы в определенном соотношении с длиной туловища или ноги (такой мерой он считал длину руки до локтя).

В современных школах живописи в качестве единой меры чаще всего принимается размер головы по вертикали. С известным допущением можно считать, что длина туловища превосходит размер головы в восемь раз. На первый взгляд это кажется странным. Но нельзя забывать, что большинство высоких людей отличаются удлиненным черепом и, и наоборот, редко можно встретить низкорослого толстяка с головой удлиненной формы.

Размеру головы пропорциональна не только длина туловища, но и размеры других частей тела. По этому принципу построены все люди, оттого-то мы в общем похожи друг на друга. Однако наши пропорции согласуются лишь приблизительно, а потому люди лишь похожи, но не одинаковы. Во всяком случае, все мы симметричны! К тому же некоторые художники в своих произведениях особенно подчеркивают эту симметрию. (Приложение 4)

Фигуры в произведениях Леонардо Да Винчи словно рождаются из тени. «Тень есть жизнь, - так напишет художник в своей «Книге о живописи», - она поражает наблюдателя тончайшими оттенками в бесконечных градациях цвета». Но удивительнее всего то, как картины тосканского гения сочетают геометрическую точность композиции с живыми движениями и чувствами персонажей.

Глава 4

Симметрия в архитектуре

“Геометрия владеет двумя сокровищами: одно из них – это

теорема Пифагора, и другое – деление отрезка в среднем и

крайнем отношении…Первое можно сравнить с мерой

золота, второе больше напоминает драгоценный камень”

Иоганн Кеплер

Стили в архитектуре. В архитектуре, как и в других видах искусства, существует понятие стиля, т.е. исторически сложившейся совокупности художественных средств и приемов.

Греческие зодчие впервые в истории строительства создали архитектурный ордер, т.е. установили четкие правила художественной обработки внешней формы конструкций, определили порядок размещения деталей и их размеры. Отличали дорический, ионический и коринфский ордеры. Все три ордера имеют одинаковые основные элементы, но отличаются друг от друга пропорциями и декоративной обработкой.

В средние века возник готический стиль. Готические здания отличаются обилием ажурных, как кружева, украшений, скульптур, орнаментов, поэтому и снаружи, и внутри они производят впечатление легкости и воздушности. Окна, порталы, своды имеют характерную стрельчатую форму. Фасады сооружений обладали зеркальной (осевой) симметрией.

Готический собор в Милане

Архитекторы Возрождения создали стиль – ренессанс, в котором использовали наследие античного искусства, греческие архитектурные ордеры. Правда, они применили их по-новому, более свободно, с отступлением от античных канонов, в других пропорциях и размерах, в сочетании с другими архитектурными элементами. Здания в стиле ренессанс были строгими по форме, с четкими прямыми линиями. Сохраняется симметрия фасадов.

Филиппо Брунеллески. Капелла Пацци (во дворе церкви Санта-Кроче во Флоренции). Строительство началось в 1429. В капелле с ее элегантным коринфским портиком и двумя куполами (в портике и самой капелле) особенно наглядно выражены пространственная свобода, цельность и ясная закономерность композиции. Выделенные цветом пилястры, антаблемент и арки четко выражают гармоничное соотношение опоры и нагрузки. Скульптурный декор интерьера был осуществлен Лукой 16ела Роббиа и Филиппо Брунеллески. Капелла является памятником архитектуры. Ныне это музей.

Андреа Палладио. Вилла Пояна близ Виченцы. 1560-е гг.

Стиль барокко, пришедший на смену ренессансу, отличается обилием криволинейных форм. Грандиозные архитектурные ансамбли (группа зданий, объединенных общим замыслом) дворцов и вилл, построенных в стиле барокко, поражают воображение обилием украшений на фасадах и внутри зданий. Прямые линии почти отсутствуют. Архитектурные формы изгибаются, громоздятся одна на другую и переплетаются со скульптурой. От этого создается впечатление постоянной подвижности форм.

Собор Смольного монастыря В.В. Растрелли. Воронцовский дворец в Санкт- Петербурге

В.В.Растрелли. Зимний дворец в Санкт- Петербурге, памятник архитектуры русского барокко.

Все здания, построенные в стиле классицизма, имеют четкие прямолинейные формы и симметричные композиции. На фоне гладких стен выступают портики и колоннады, которые придают сооружениям торжественную монументальность и парадность. Декоративное убранство из барельефов и статуй оживляют облик зданий. Мастера классицизма сознательно заимствовали приемы античности и ренессанса, применяли ордеры с античными пропорциями и деталями.

Казанский собор в Санкт-Петербурге построен для перенесения в него древней иконы Казанской богоматери, по ее имени и назван. Здание собора является монументальным памятником архитектуры русского классицизма (архитектор А. Н. Воронихин). Грандиозная полукруглая колоннада из 96 поставленных в четыре ряда коринфских колонн с шестиколонным портиком в центре примыкает к боковому (северному) входу собора и обращена к Невскому проспекту.

Адмиралтейство в Санкт-Петербурге (центральная часть). Архитектор А. Д. Захаров. Здание Адмиралтейства является выдающимся памятником русской архитектуры. Заложено в 1704 как корабельная верфь Петром I, ему же принадлежал и основной замысел сооружения.

Глава 5

Использование симметрии в декоративно – прикладном искусстве

Декоративно прикладное искусство, область декоративного искусства: создание художественных изделий, имеющих практическое назначение в общественном и частном быту, и художественная обработка утилитарных предметов (утварь, мебель, ткани, орудия труда, средства передвижения, одежда, украшения, игрушки и т. д.). При обработке материалов (металл, дерево, керамика, стекло, текстиль и др.) в декоративно-прикладном искусстве используются литье, ковка, чеканка, гравирование, резьба, роспись, инкрустация, вышивка, набойка и т. д. Произведения декоративно-прикладного искусства составляют часть предметной среды, окружающей человека, и эстетически ее обогащают. Они обычно тесно связаны с архитектурно-пространственным окружением, ансамблем (на улице, в парке, в интерьере) и между собой, образуя художественный комплекс. Возникнув в глубокой древности, декоративно-прикладное искусство стало одной из важнейших областей народного творчества, его история связана с художественным ремеслом, художественной промышленностью, с деятельностью профессиональных художников и народных мастеров, с нач. 20 в. также с художественным конструированием.

5.1 ОРНАМЕНТЫ

Искусство орнамента содержит в неявном виде наиболее

древнюю часть известной нам высшей математики.

Герман Вейль

 

Орнамент (от лат. Ornamentum – украшение) – узор, состоящий из ритмически упорядоченных элементов. Возникновение орнамента относится к эпохе палеолита и связано с обрядами. Теперь же орнамент играет декоративную роль.

Среди большого количества видов орнаментов выделяются круговые, линейные и плоские орнаменты

5.1.1 РОЗЕТКИ 

Чаще всего различные виды симметрии встречаются в круглых орнаментах, которые называются розетками. Они используются в резьбе по дереву, в настенной лепке, в вышивках и в ковровых изделиях. Обычно основной формой розетки служит круг, разбитый на равные части. Рисунок, выполненный в одной части симметрично повторяется в других частях круга. Примером розетки является снежинка, вырезанная из салфетки. 

Розетка имеет 6 осей симметрии

Вторая розетка имеет 4 оси симметрии

Третья розетка имеет 8 осей симметрии

Использование орнаментов (Приложение 5)

Линейные орнаменты называются бордюрами.

5.1.2 БОРДЮР – это периодически повторяющийся рисунок на длинной ленте. Бордюры используются в настенных росписях, в чугунном литье для оград, мостов, набережных. Рисунки в виде бордюров наносятся на ткани, мебель, обои и т.д.

Любой бордюр может быть совмещён сам с собой параллельным переносом. При рисовании бордюров кроме параллельного переноса используется симметрия относительно прямой, центральная симметрия. (Приложение 6)

Всего существует семь типов бордюров.

БОРДЮР ПЕРВОГО ТИПА. Это самый простой бордюра получатся при параллельном переносе произвольного рисунка на один и тот же направленный отрезок (вектор). Схематично этот тип бордюра можно представить так, как показано.

 

 

 

 

 

 

 

  БОРДЮР ВТОРОГО ТИПА. Бордюр этого типа схематично показан.

 

 

 

 

 

 

1.  

Прямая а на этом рисунке является осью симметрии бордюра. Чтобы получить бордюр этого типа, нужно взять произвольный рисунок, отразить его относительно прямой объединить с данными, а затем полученный рисунок смещать параллельным переносом.

Проделаем это с элементом, который показан на рисунке. Здесь тонкой линией отмечена ось симметрии а, а параллельный перенос задан направленным отрезком. Отразим элемент относительно прямой а. В объединении полученного элемента с первоначальным получим уже более сложный рисунок. Сместим его несколько раз параллельным переносом, получим бордюр второго типа.

 

 

 

 

 

 

 

 

 

 

 

 

БОРДЮР ТРЕТЬЕГО ТИПА.   

Чтобы получить бордюр этого типа, нужно начальный элемент отразить от прямой а, затем полученный рисунок сместить параллельным переносом на направленный отрезок б. Объединение данного элемента и полученного смещаем параллельным переносом на направленный отрезок с.

Рассмотрим получение бордюра из элемента, показанного на рис. 1 Отразим его по прямой а и сместим полученный рисунок параллельным переносом на направленный отрезок б. Получим новый элемент бордюра (рис. 2).

 

 

 

 

 

 

Рис 1

Рис.2

Смещая его параллельным переносом на направленный отрезок с, получим бордюр третьего типа (рис. 3).

 

 Рис.3

 

 

Пусть начальный элемент бордюра представлен на рисунке 4. Отразим его от прямой а и сместим полученный элемент параллельным переносом на направленный отрезок б. Объединив оба рисунка, получим новый рисунок (рис. 5). Смещая его параллельным переносом на направленный отрезок с, получим бордюр третьего типа (рис. 6).

 

 

 

 

 

 

 

Рис. 4 рис. 5

 

рис. 6

БОРДЮР ЧЕТВЁРТОГО ТИПА. Этот тип бордюра схематично показан. В преобразовании первоначального элемента участвует осевая симметрия с осью а, перпендикулярной краю бордюра. Объединив данный элемент с симметричным ему относительно прямой а, смещаем полученный рисунок параллельным переносом на направленный отрезок б. Если полученный рисунок отражать от второй оси, то получим тот же результат.

 

 

 

 

 

 

 

 

Аналогичным способом получен бордюр, изображённый на рисунке.

 

 

БОРДЮР ПЯТОГО ТИПА. Схема бордюра пятого типа показана. Светлыми кружочками отмечены центры симметрии. Прямая, проходящая через эти центры, переходит в себя при отражении от указанных центров.

 

  БОРДЮР ПЯТОГО ТИПА. Схема бордюра пятого типа показана на рис. 7. Светлыми кружочками отмечены центры симметрии. Прямая, проходящая через эти центры, переходит в себя при отражении от указанных центров.

 

 

 

 

1.    Рис. 7

Пусть дан элемент, изображённый

на рисунке 8. Светлым кружком также отмечен центр симметрии. Отразим этот элемент от указанного центра симметрии. Объединив рисунки, получим следующий элемент бордюра (рис. 9). Смещая его параллельным переносом на направленный отрезок б, получим бордюр пятого типа (рис. 10).

 

 

 

 

Рис. 8 рис. 9

 

 

 

 

  

Рис. 10

БОРДЮР ШЕСТОГО ТИПА.

Начальный элемент бордюра изображён (рис11.).Над ним совершаются преобразования симметрии относительно точки и относительно прямой. После объединения его с центрально симметричным, получим новый элемент, представленный на рисунке (рис.12). Объединим, последний с симметричным относительно прямой а, получим _рис.13).

 

 

 

 

 

Рис.11 рис.12 рис.13

Смещая параллельным переносом на отрезок б, получим бордюр шестого типа (рис.14).

 

 

   

  Рис.14

 

БОРДЮР СЕДЬМОГО ТИПА.

Схема бордюров этого типа показана на рисунке 15.Основной элемент бордюра, который смещается итоге параллельным переносом, получается из первоначального с помощью двух осевых симметрий со взаимно перпендикулярными осями.

 

 

 

 

 

  Рис

Рис.15

Рассмотрим получение бордюра данного типа из простейшего элемента, приведённого на рис 16. Для этого отразим данный элемент от оси а. Затем объединение данного и полученного элементов отразим от оси б. Получим элемент, показанный на рисунке 17.

 

 

 

Рис.16 рис.17

Смещая эту фигуру параллельным переносом на направленный отрезок с, получим бордюр седьмого типа. рис.18

 

 

 

 

 

Рис.18

1. 5.1.3 ПАРКЕТЫ

 

Кроме рассмотренных орнаментов существуют плоские орнаменты, заполняющие лист бумаги (плоскость) без промежутков. Такие орнаменты называются ПАРКЕТАМИ. Это такие же паркеты, как в наших квартирах, как орнаменты на линолеуме, как рисунки на обоях. Тетрадный лист в клеточку представляет собой простейший паркет. Элементом паркетом здесь является квадрат. На этой решётке можно составить и другие пакеты (т.е. используя другие элементы паркета, паркеты можно называть решётками). Можно придумать сотни, тысячи разных элементов паркетов. Некоторые из них изображены на рис.

 

 

 

 

 

 

Существуют такие паркеты, у которых несколько элементов образуют фигуру, подобную элементу паркета. Примеры таких паркетов приведены на рисунке

 

 

 

 

 

 

  Всего существует 17 видов симметрии сетчатых орнаментов. Первые семь из них допускают создание интересных паркетов без прямолинейных контуров.

 

 

 

 

  

Простейшим видом паркета является такой, в котором плоскость заполнена фигурами с помощью параллельного переноса.

 Паркет называется правильным, если его можно наложить на себя так, что любая заданная его вершина наложится на любую другую наперёд заданную вершину.

Уже пифагорейцам было известно, что имеются три вида правильных многоугольников, которыми можно полностью замостить плоскость без пробелов и перекрытий, - треугольник, квадрат и шестиугольник.

  Сколько же всего правильных паркетов?

Легко видеть, что вообще паркетов – не обязательно правильных – существует бесчисленное множество. Однако, подобно тому, как при бесчисленном множестве многогранников вообще существует лишь конечное число правильных паркетов:

Паркеты с тремя многоугольниками вершине. Здесь возможно три случая: а) 3 одинаковых многоугольника б) два одинаковых и один отличный в) три разных многоугольника;

 

 

 

 

 

 

 

 

 

 

Вывод

Мы рассмотрели симметрию в целом, как соразмерность, пропорциональность, одинаковость в расположении частей в живой и неживой природе, в словах, архитектуре, живописи и самой математике. Симметрия присутствует везде: в регулярности смены дня и ночи, времён года, в ритмичном построении стихотворения, там, где присутствует какая-то упорядоченность и регулярность.

Исследования, показали, что симметрия является одним из принципов гармонического построения мира. «Сфера влияния» симметрии поистине безгранична. Она присутствует в нашей жизни буквально во всем, но мы настолько к ней привыкли, что не замечаем этого. Всюду она определяет гармонию природы, мудрость науки и красоту. Мы считаем, что как бы не развивался наш мир в дальнейшем, симметрия в нем будет преобладать.

СПИСОК ЛИТЕРАТУРЫ

1. Гильде В. Зеркальный мир. – М.: Мир, 2014 г.

2. Гаспаре Де Фиори. Мастерская рисунка. – М: ООО «Де Агостини», 2007 г.

3. Современный словарь иностранных слов. – М.: Русский язык, 1993 г.

4. Советский энциклопедический словарь –

5. Конышева Н.М. Технология 3 и 4 классов. – М: Ассоциация 21 век, 2001 г.

6. Урманцев Ю.А. Симметрия природы и природа симметрии – М.: Мысль, 2014 г.

Интернет ресурсы

1. http://www.portal.net.ua/~genplan 

2. http://festival.1september.ru/

3. http://www.bymath.net/index.html

4. irinmorozova.narod.ru

29