Теория по математическому анализу

Теория

Наибольшее и наименьшее значения функции двух переменных в замкнутой области

• Пусть функция z=f(x,y) определена и непрерывна в некоторой ограниченной замкнутой области D. Пусть в этой области заданная функция имеет конечные частные производные первого порядка (за исключением, быть может, конечного количества точек). Чтобы найти наибольшее и наименьшее значения функции двух переменных в данной замкнутой области требуется выполнить три шага простого алгоритма.

Алгоритм поиска наибольшего и наименьшего значений функции z=f(x,y) в замкнутой области D.

• Найти критические точки функции z=f(x,y), принадлежащие области D. Вычислить значения функции в критических точках.
• Исследовать поведение функции z=f(x,y) на границе области D, найдя точки возможного наибольшего и наименьшего значений. Вычислить значения функции в полученных точках.
• Из значений функции, полученных в предыдущих двух пунктах, выбрать наибольшее и наименьшее.

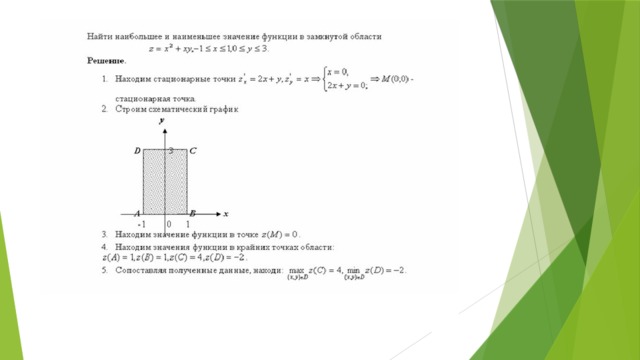
Метод множителей Лагранжа

• Метод множителей Лагранжа - это метод решения задач на условный экстремум; метод множителей Лагранжа заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — так называемой функции Лагранжа.

Для задачи об экстремуме функции

функция Лагранжа имеет вид

где

множители Лагранжа

Если x*-точка локального минимума в поставленной задаче, то существуют множители Лагранжа , не равные одновременно нулю, т.е.

, и такие, что выполнены условия:

а). Стационарности

или

б). Дополняющей нежесткости

в). Неотрицательности (согласования знаков)

г). допустимости

пример

• Решить экстремальную задачу

• Решение

Составим функцию Лагранжа:

Производная по направлению

• Теорема. (О вычислении производной по направлению)

Если и u = u(M) дифференцируема в точке M0, то

• Физический смысл производной по направлению: скорость изменения функции (определяющей скалярное поле) в данном направлении l.

Составить уравнение касательной плоскости к поверхности

Уравнение касательной плоскости к поверхности

В точке (Х0, Y0, Z0) имеет вид:

Решение

Подставим эти значения в уравнение касательной плоскости:

Ответ:

Неявно заданная функция

Если функция задана уравнением у=f(х), разрешенным относительно у , то функция задана в явном виде ( явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0,не разрешенного относительно у.

Всякую явно заданную функцию у=f(х) можно записать как неявно заданную уравнением f(х)-у=0, но не наоборот.

Не всегда легко ,а иногда и невозможно разрешить уравнение относительно у (например у+2х+cosy-1=0 или 2у-х+у=0).

Если функция задана неявно , то для нахождения производной от у по х нет необходимости рахрешать уравнение относительно у: достаточно продифференцировать это уравнение по х,рассматривая при этом у как функцию х ,и полученное затем уравнение разрешить относительно .

Производная неявной функции выражается через аргумент х и функцию у.

Пример: Найти производную функции у, заданную уравнением

Решение : Функция у задана неявно . Дифференцируем по х равенство

Из полученного соотношения :

Касательная плоскость и нормаль

Решение: Составим уравнение плоскости по точке и двум неколлинеарным векторам:

Определитель удобнее всего раскрыть по первому столбцу:

Раскрываем определители второго порядка:

На первом месте у нас находится знак «минус». Хорошим тоном считается убрать наглеца, в этих целях меняем знак у каждого слагаемого. Проводим дальнейшие упрощения и получаем уравнение плоскости:

Сократить здесь ничего нельзя, поэтому:

Ответ: