Тема урока: « Свойства степени с натуральным показателем»
Цели:
Образовательная: Обеспечить повторение, обобщение и систематизацию знаний по теме, закрепить и усовершенствовать навыки простейших преобразований выражений, содержащих степени с натуральным показателем, создать условия контроля усвоения знаний и умений
Развивающая: Способствовать формированию умений применять приёмы обобщения, сравнения, выделения главного, содействовать воспитанию интереса переноса знаний в новую ситуацию, развитие математического кругозора, речи, внимания и памяти, развитие учебно-познавательной деятельности;
Воспитательная: Воспитание интереса к математике, активности, организованности, воспитывать умений асом и взаимоконтроля своей деятельности, формирование положительной мотивации учения, культуры общения.
Методы обучения : Объяснительно – иллюстративный, словесный, практический, ИКТ
Ход урока:
1.Орг. момент
Добрый день, ребята. Ребята, я хочу вам пожелать плодотворно поработать на уроке, внимательно обдумывать ответы на поставленные вопросы, не торопиться, не перебивать, уважать одноклассников и их ответы. Удачи вам!
2.Актуализация опорных знаний и вхождение в тему урока
На экране вы видите ребусы, в которых зашифрованы ключевые слова сегодняшнего урока. Вы работаете в парах. Разгадайте их. Кто готов, поднимает руку.
Ребята, вы правильно отгадали ребусы. Эти слова: степень, свойства. А теперь, используя отгаданные слова – подсказки, сформулируйте тему сегодняшнего урока.
Правильно. Откройте тетради и запишите число и тему урока «Свойства степени с натуральным показателем».
Цель урока: повторить и обобщить наши знания по данной теме, ликвидировать имеющиеся пробелы,
3.Устная работа
Эпиграф к уроку слова великого русского учёного М.В.Ломоносова « Пусть кто–нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь».
- Как вы думаете, прав учёный?
- Для чего нам нужны степени? Ребята, свойства степени с натуральным показателем довольно часто применяются при нахождении значений выражений, при преобразованиях выражений.
- Где они нашли широкое применение? (в физике, астрономии) Степени в физике используются для удобной записи очень малых и очень больших чисел
Взрослый человек состоит примерно из 7 октиллионов атомов
7 000 000 000 000 000 000 000 000 000 = 7∙10²7
Масса Земли 6 септиллионов 6 000 000 000 000 000 000 000 000 кг = 6∙10²4 кг
Масса Солнца 2 нониллиона 2 000 000 000 000 000 000 000 000 000 000 кг = 2∙1030 кг
- А теперь давайте повторим, что же такое степень?
- Как называются а и n в записи степени?
- Какие действия можно выполнять со степенями?
у4 у3 у = у8
х7 : х4 х0 = х3
(х5) 6 = х30
((х2 )3) 4 = х24
86 / 84 = 82 = 64
4. Перенос приобретенных знаний, их первичное применение в новых или изменённых условиях, с целью формирования умений. Предлагаю вам следующую работу: у вас на партах карточки. Вам нужно выполнить задания, т.е. записать ответ в виде степени с основанием с, и вы узнаете фамилию и имя великого французского математика, который ввёл общепринятое в настоящее время обозначение степеней. Вы работаете по вариантам (1 и 2). После того, как вы решите все примеры, обсудите со своим соседом по парте, какие имя и фамилия у вас получились. Ответ: Рене Декарт.
|
| Вариант 1 |
| Вариант 2 |
| 1. | С5 • С3 | 6. | С7 : С5 |
| 2. | С8 : С6 | 7. | (С4)3 • С |
| 3. | (С4)3 | 8. | С4 • С5 • С0 |
| 4. | С5 • С3 : С6 | 9. | С16 : С8 |
| 5. | С14 • С8 | 10. | (С3)5 |
| Р | Ш | М | Ю | К | Н | А | Т | Е | Д |
| С8 | С5 | С1 | С40 | С13 | С12 | С9 | С15 | С2 | С22 |
Рассказ о биографии Рене Декарта Родился Рене Декарт 31 марта 1596 года во Франции в городе Лаэ, провинция Турень. Сейчас этот город носит его имя. 17 век - век гениев. Декарт - фигура первостепенной величины, чрезвычайно разносторонний человек, математик, геометр. В области естествознания занимался оптикой, физиологией и т.д. Родоначальник философии Нового Времени. В своём труде «Геометрия» (1637) Рене Декарт впервые ввёл показатель степени, которым пользуются и сейчас.
4. Решение заданий учащимися под контролем учителя.
А теперь посмотрим, справитесь ли вы с заданием посложнее. При его выполнении нужно применить несколько известных вам свойств степеней.
(52)3 · 5 : 54
(23)7 : (25)3
(42)4 : 45· 40
(34)2 · (32)3 : 310
Решение заданий из учебника № 558 (б, в), 560 (ж, з), дополнительно 560 (а, б, в)
Решение заданий ВПР
Найдите значение выражения 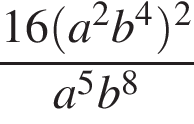 при
при  и
и 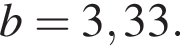
Найдите значение выражения 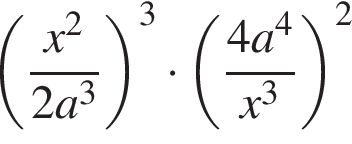 при
при 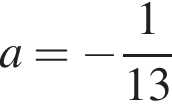 и
и 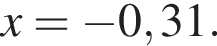
Найдите значение выражения 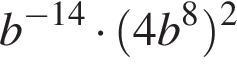 при
при 
Что произошло с понятием степени в дальнейшем, мы с вами можем предсказать сами. Для этого попробуйте ответить на вопрос: можно ли число возвести в отрицательную степень или дробную?
Исаак Ньютон в 1677 году впервые описал действие возведения числа в отрицательную и дробную степени и обобщил формулы для всех видов степеней. Но это предмет нашего будущего изучения.
7. Итоги урока
А теперь подведём итог. У вас на парте листочки с заданиями Слева указаны начала определений, справа - окончания определений. Соедините линиями верные высказывания.
|
|
| а) При умножении степеней с одинаковыми основаниями … |
| 1)основанием степени |
| б) При делении степеней с одинаковыми основаниями …. | 2) Показатель степени |
| в) Число а называют | 3) произведение n множителей, каждый из которых равен а. |
| г) При возведении степени в степень … | 4)… основание остается прежним , а показатели складываются. |
| д)Степенью числа а с натуральным показателем n, большим 1, называется | 5)… основание остается прежним, а показатели перемножаются. |
| е) Число n называют | 6) Степенью |
| ж) Выражение а n называют | 7)…основание остается прежним , а показатели вычитаются. |
2.Теперь, поменяйтесь листочками с соседом по парте, оцените его работу после её проверки.
Давайте проверим, правильно ли вы выполнили задание.
Оцените работу:
7 баллов – молодец
6 баллов – очень хорошо
5 баллов – хорошо
4 балла – не очень хорошо
3 балла – плохо
0-2 балла – очень плохо.
Поставьте рядом с таблицей количество набранных баллов
8. Домашнее задание: повторить правила п. 19, 20, № 559 (а, г), 560 (г, д, е) стр. 125
9. Оценки за урок.
Наш урок закончен. Спасибо всем за работу на уроке!
2

















