Урок по теме: Различные методы решения уравнений
Цель: обобщить, систематизировать, углубить знания и умения решения уравнений, применяя различные методы, формировать навыки их творческого применения во время решения уравнений разных степеней сложности. Развивать логическое мышление, память, внимание; воспитывать трудолюбие, самостоятельность.
Тип урока: обобщения и систематизации знаний.
Ход урока
I.Актуализация опорных знаний.
1. Конкурс – разминка «Мозговой штурм».
Учащиеся объединяются в четыре группы.
За каждый правильный ответ группа получает дополнительный балл.
Вопросы
-
Какое равенство называется уравнением?
-
Как записать в общем виде уравнение с одной переменной?
-
Что значит решить уравнение?
-
Какие виды уравнений вы знаете?
-
Какие способы решения уравнений вы знаете?
-
Какие стандартные типы уравнений вы знаете?
2. Устное решение уравнений.
1) Х8+5Х6+Х4+10Х2+95 = 0.
(корней нет, т.к. левая часть больше 0)
2) Х4 – 5Х2+7 = 0.
(корней нет, Д
3) 3Х2- 5Х + 2 = 0.
( 1; 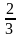 )
)
4) Х4 – 5Х2+ 4 = 0.
(±1; ±2)
5) Х4+ 2Х2+ 4 = cos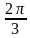 .
.
(корней нет, левая часть больше нуля, 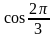
II. Проверка домашнего задания.
Учащиеся объединены в группы за методами решения уравнений. Они должны были подобрать уравнение, которое решается заданным методом. Каждая группа называет свой метод решения уравнений и объясняет, для решения каких уравнений он используется. Пример записывается на доске.
I группа. Разложение левой части на множители, когда правая равна 0.
Метод разложения на множители применяется для решения тригонометрических, показательных, логарифмических и др. уравнений, правая часть которых равна 0, а левую можно разложить на множители.
Пример. 3х3+ 4х2+ 4х +3 = 0.
3(х3+ 1) + 4х (х + 1) = 0,
3(х + 1) (х2- х + 1) + 4х (х + 1) = 0,
(х + 1) (3х2- 3х + 3 + 4х) = 0,
(х + 1) (3х2+ х + 3) = 0,
х = -1 или 3х2+ х + 3 = 0,
Д
Ответ. – 1.
II группа. Метод введения новой переменной.
Метод введения новой переменной применяется практически в уравнениях всех видов:
тригонометрических, показательных, логарифмических, иррациональных и алгебраических.
Пример. х2+2х +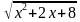 = 12.
= 12.
х2+ 2х +8 + 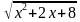 = 20.
= 20.
Пусть 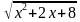 = а, а
= а, а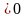 , тогда
, тогда
а2 + а – 20 = 0,
а1 = - 5 посторонний корень, а2 = 4.
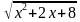 = 4,
= 4,
х2+ 2х + 8 = 0,
х1= - 4, х2 = 2.
Ответ. -4; 2.
III группа. Приведение уравнений к стандартным типам.
Метод приведения уравнения к стандартному виду применяется, когда данное тригонометрическое, логарифмическое или показательное уравнение можно привести к стандартному виду, т. е. к уравнению квадратному, биквадратному, симметричному или возвратному.
Пример. 72х+1+ 3 · 28х- 42х + 1= 0.
7 · 72х+ 3 · 7х· 4х-4 · 42х= 0.
Разделим обе части уравнения на 42х, имеем:
7 ·( 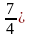 2х+ 3 · (
2х+ 3 · (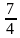 )х-4 = 0.
)х-4 = 0.
Пусть (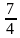 )х= а, а
)х= а, а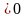 , тогда 7а2+ 3а – 4 = 0,
, тогда 7а2+ 3а – 4 = 0,
а1 = -1 - посторонний корень, а2= 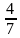 .
.
Следовательно, (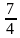 )Х=
)Х= 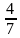 ,
,
Х = - 1.
Ответ. – 1.
IV группа. Комбинирование разных методов.
Если какое-то из уравнений невозможно решить одним из ранее перечисленных методов, то для его решения комбинируют разные методы.
Пример. 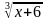 +
+ 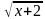 = 4.
= 4.
Пусть 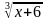 = а, х+6 =а3, х+2 = а3- 4.
= а, х+6 =а3, х+2 = а3- 4.
Имеем:
а + 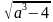 =4,
=4,
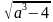 = 4 – а,
= 4 – а,
а3- а2+ 8а – 20 = 0.
Числа ±1; ±2; ±4; ±5; ±10; ±20 могут быть корнями уравнения. Устной проверкой устанавливаем, что 2 является корнем уравнения.
(а3- а2+ 8а – 20): (а – 2) = а2+ а + 10.
Следовательно, (а – 2) (а2+ а + 10) = 0,
а = 2 или а2+ а + 10 = 0,
Д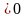 , корней нет.
, корней нет.
Если а = 2, то 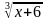 = 2,
= 2,
х + 6 =8,
х = 2.
Ответ. 2.
III. Решение уравнений.
Во время решения уравнения учащиеся передают мнимый «микрофон» тому, кто предлагает следующий шаг решения.
Решить уравнение
(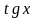 + 2)(
+ 2)(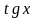 +3)(
+3)(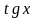 +8)(
+8)(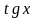 + 12) = 4
+ 12) = 4  х.
х.
Решение
1)Введем новую переменную 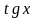 = t. Тогда
= t. Тогда
(t  2)(t +3)(t + 8)(t + 12) = 4t2.
2)(t +3)(t + 8)(t + 12) = 4t2.
2) Перемножим попарно скобки. Имеем:
(t2+ 14t + 24) (t2+ 11t + 24) = 4t2.
3) Разделим обе части уравнения на t2, t≠0.
(t + 14 +  )(t + 11 +
)(t + 11 +  ) = 4.
) = 4.
4) Вводим новую переменную t +  =y. Получим:
=y. Получим:
(у + 14) (у +11) = 4,
у2+ 25у + 154 – 4 = 0,
у2 + 25у + 150 = 0,
у1= -10, у2= -15.
5) Решим уравнения:
t +  = -10 или t +
= -10 или t +  = -15.
= -15.
a) t2+ 10t + 24 = 0.
t1= -6. t2= -4.
б) t2+ 15t + 24 = 0,
Д = 225 – 96 = 129,
t1=  ; t2=
; t2= .
.
6) Решить уравнение, подставив вместо t его значение.
а) 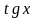 = -6, х1 = - arc
= -6, х1 = - arc + πn, nϵ Z ;
+ πn, nϵ Z ;
б)  = - 4, х2 = -arc
= - 4, х2 = -arc + πк, кϵ Z ;
+ πк, кϵ Z ;
в)  =
=  , х3= - arc + πm, mϵ Z;
, х3= - arc + πm, mϵ Z;
г) 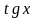 =
=  , х4= -arc
, х4= -arc +πl, lϵ Z .
+πl, lϵ Z .
Самостоятельная работа.
Каждая группа должна решить два уравнения: одно – методом своей группы, второе – другими методами. Уравнение, решенное методом группы, остается, его можно использовать при проверке, второе уравнение отдают той группе, методом которой его решали.
I группа
Решить уравнение  +
+  +
+  = 0.
= 0.
Решение
2 +
+  = 0,
= 0,
= 0,

х = nϵZ.
nϵZ.

х = ± 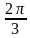 + 2πк, кϵ Z.
+ 2πк, кϵ Z.
II группа
Решить уравнение (х – 2) (х – 3) (х – 4) (х – 6) = 30 х2.
Решение
(х2- 8х + 12) (х2- 7х + 12) = 30х2,
(х +  – 8) (х +
– 8) (х +  – 7) = 30.
– 7) = 30.
Пусть х +  = t , тогда (t – 8) (t – 7) = 30,
= t , тогда (t – 8) (t – 7) = 30,
t2- 15t + 56 – 30 = 0,
t2- 15t + 26 = 0,
t1= 13, t2= 2,
х +  = 13,
= 13,
х2- 13х + 12 = 0,
х1= 1, х2= 12.
х + = 2,
= 2,
х2- 2х + 12 = 0, корней нет.
III группа
Решить уравнение  4х) +
4х) +  = 8.
= 8.
Решение
 (4х) + 2
(4х) + 2 -
-  = 8,
= 8,
 (4х) + 2
(4х) + 2 = 11,
= 11,
 (4х) + 2(
(4х) + 2( – 2) = 11,
– 2) = 11,
 (4х) + 2
(4х) + 2  – 15 = 0.
– 15 = 0.
Пусть  = а, тогда а2+ 2а – 15 = 0, а1= - 5; а2= 3.
= а, тогда а2+ 2а – 15 = 0, а1= - 5; а2= 3.
 = - 5, или
= - 5, или  = 3,
= 3,
4х =  , 4х = 8,
, 4х = 8,
х =  . х = 2.
. х = 2.
IV группа
Решить уравнение  x
x x – 15
x – 15  x + 36
x + 36 x = 0.
x = 0.
Решение
 x(
x( x - 15
x - 15 + 36
+ 36  x) = 0,
x) = 0,
 x = 0,
x = 0,
x =  , nϵ Z.
, nϵ Z.
 x – 15tgx + 36 = 0.
x – 15tgx + 36 = 0.
Пусть tg x = t, тогда t2- 15t + 36 = 0,
t1=3, tgx = 3, x = аrctg3 + πm, mϵ Z.
V. Итог урока.
Есть ли универсальный способ решения уравнений?
Какой из способов решения уравнений используется чаще других?
На каком из способов вы хотели бы дольше остановиться и какие виды уравнений еще рассмотреть?
VI. Домашнее задание.
Учащимся раздаются карточки с заданиями. Они выбирают четыре уравнения, которые можно решить разными методами.
-
 +
+  = 4; 6)
= 4; 6)  – 10·3х= 2·3х+3- 11·22х;
– 10·3х= 2·3х+3- 11·22х;
2) ; 7) 3·16х+ 2·81х= 5·62х;
3) +
+  = 2; 8)
= 2; 8)  +
+  = ;
= ;
4) 3 -
-  + 1 = 0; 9) (3х2+ 7х – 2)(8х2+ 7х – 2) = 24х4;
+ 1 = 0; 9) (3х2+ 7х – 2)(8х2+ 7х – 2) = 24х4;
5)  + 3
+ 3 = 2; 10)
= 2; 10)  =
=  .
.






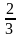 )
)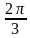 .
.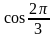
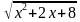 = 12.
= 12.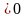 , тогда
, тогда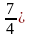 2х+ 3 · (
2х+ 3 · (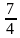 )х-4 = 0.
)х-4 = 0.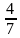 .
.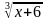 +
+ 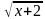 = 4.
= 4.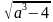 =4,
=4,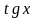 + 2)(
+ 2)(


















