Вариант № 4
1. Найдите значение выражения 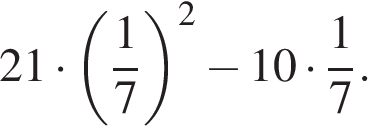
2. В таблице представлены нормативы по технике чтения в 3 классе.
| Отметка | Количество прочитанных слов минуту |
| Первое полугодие учебного года | Второе полугодие учебного года |
| «2» | 59 и менее | 69 и менее |
| «3» | 60−69 | 70−79 |
| «4» | 70−79 | 80−89 |
| «5» | 89 и более | 99 и более |
Какую отметку получит третьеклассник, прочитавший в апреле 68 слов за минуту?
В ответе укажите номер правильного варианта.
1) «2»
2) «3»
3) «4»
4) «5»
3. На координатной прямой точками отмечены числа 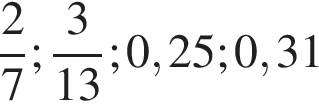

Какому числу соответствует точка D?
1)
2)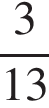
3)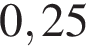
4)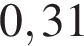
5. На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим значением температуры и наименьшим.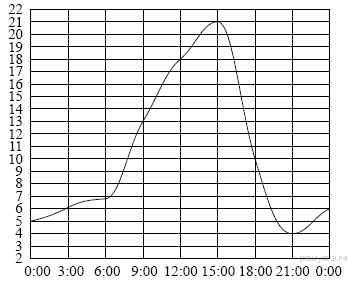
6. Решите уравнение 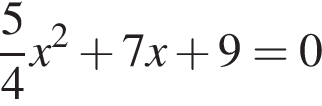
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
7. Чайник, который стоил 800 рублей, продаётся с 5%-ой скидкой. При покупке этого чайника покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?
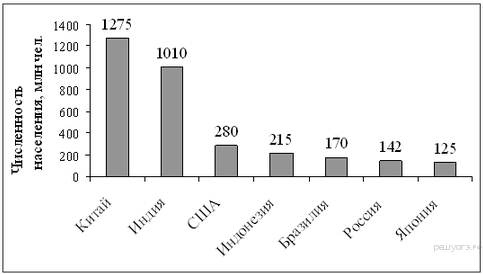
8. На диаграмме представлены некоторые из крупнейших по численности населения стран мира.
Численность населения какого государства примерно в 6 раз меньше численности населения Индии?
В ответе напишите численность населения этой страны в млн чел.
9. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.
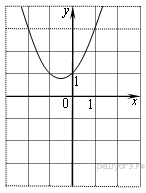
10. Найдите значение 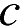 по графику функции
по графику функции 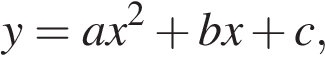 изображенному на рисунке.
изображенному на рисунке.
11. Найдите сумму всех положительных членов арифметической прогрессии 11,2; 10,8; …
12.Найдите значение выражения 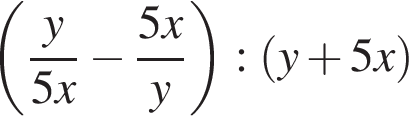 при
при 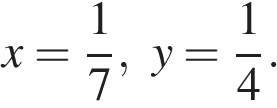
13. Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 588 ватт, а сила тока равна 7 амперам.
14. Укажите неравенство, решением которого является любое число.
1) x2 + 70 0
2) x2 − 70 0
3) x2 + 70
4) x2 − 70
15. Найдите периметр прямоугольного участка земли, площадь которого равна 800 м2 и одна сторона в 2 раза больше другой. Ответ дайте в метрах.
16. 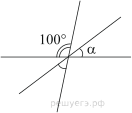
Углы, отмеченные на рисунке одной дугой, равны. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
17.
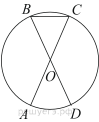
В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 50°. Найдите вписанный угол ACB. Ответ дайте в градусах.
18. В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.
19.
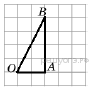 Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.
Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.
20.
Какие из следующих утверждений верны?
1) Около всякого треугольника можно описать не более одной окружности.
2) В любой треугольник можно вписать не менее одной окружности.
3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.
4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.
Если утверждений несколько, запишите их номера в порядке возрастания.
21.
Сократите дробь 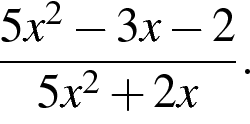
22. Моторная лодка прошла 36 км по течению реки и вернулась обратно, потратив на весь путь 5 часов. Скорость течения реки равна 3 км/ч. Найдите скорость лодки в неподвижной воде.
23.Постройте график функции 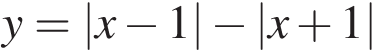 и найдите все значения k, при которых прямая
и найдите все значения k, при которых прямая  имеет с графиком данной функции ровно одну общую точку.
имеет с графиком данной функции ровно одну общую точку.
24.
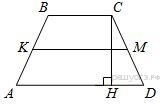
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
25. В окружности через середину O хорды BD проведена хорда AC так, что дуги AB и CD равны. Докажите, что O — середина хорды AC.
26. Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 8 и MB = 13. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Решение задач № 22-26
№ 22 Решение.
Обозначим 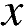 км/ч искомую скорость. По течению реки лодка двигалась ч.
км/ч искомую скорость. По течению реки лодка двигалась ч.
Против течения лодка шла ч. Получаем уравнение
.
Решим его:
Корни квадратного уравнения: 15 и −0,6. Следовательно, скорость лодки равна 15 км/ч.
Ответ: 15 км/ч.
№ 23 Решение.
Раскрывая модули, получаем, что при  функция принимает вид
функция принимает вид  при
при  функция принимает вид а при
функция принимает вид а при  функция принимает вид
функция принимает вид 
График функции изображён на рисунке.
Прямая  имеет с графиком данной функции ровно одну общую точку при
имеет с графиком данной функции ровно одну общую точку при  принадлежащем множеству
принадлежащем множеству
Ответ:
№ 24 Решение.
В трапеции средняя линия равна полусумме оснований, поэтому можем найти большее основание  зная
зная  и
и 
Проведём в трапеции вторую высоту  Трапеция равнобедренная, поэтому Рассмотрим два треугольника:
Трапеция равнобедренная, поэтому Рассмотрим два треугольника:  и
и  , они прямоугольные, имеют равные углы и
, они прямоугольные, имеют равные углы и  равно
равно  следовательно, эти треугольники равны. Таким образом, равны отрезки
следовательно, эти треугольники равны. Таким образом, равны отрезки  и
и 
Также рассмотрим четырёхугольник , все углы в нём — прямые, следовательно, это прямоугольник, значит,
Теперь найдём длину отрезка 
Ответ: 12.
№25 Решение.
Вписанные углы ADB, CBD , ACB и DAC опираются на равные дуги, значит, они равны.
Получаем, что треугольники СOВ и AOD подобны по двум углам; их коэффициент подобия равен BO:OD. Поскольку BO = OD , эти треугольники равны, следовательно, AO = OC.
№ 26 Решение.
Угол  равен половине дуги на которую он опирается, поскольку это угол, образованный касательной к окружности и секущей, проведённой через точку касания. Угол
равен половине дуги на которую он опирается, поскольку это угол, образованный касательной к окружности и секущей, проведённой через точку касания. Угол  — вписанный, поэтому он также равен половине дуги, на которую опирается. Углы
— вписанный, поэтому он также равен половине дуги, на которую опирается. Углы  и
и  опираются на одну и ту же дугу, следовательно, они равны. Рассмотрим треугольники
опираются на одну и ту же дугу, следовательно, они равны. Рассмотрим треугольники  и угол
и угол  — общий, углы
— общий, углы  и
и  равны, следовательно, треугольники подобны, откуда Биссектриса угла делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам: Получаем:
равны, следовательно, треугольники подобны, откуда Биссектриса угла делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам: Получаем:
Найдём 
Ответ:







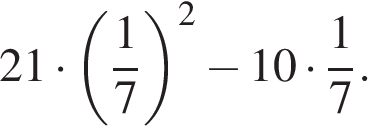





 Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.
Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.











