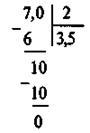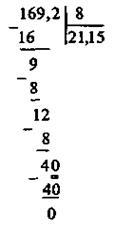Деление десятичных дробей на натуральное число

Тема. Деления десятичных дробей

Цель: установить правило деления десятичной дроби на натуральное число; формировать умение применять это правило в различных ситуациях деления десятичной дроби на натуральное число.

Ход урока

I. Актуализация опорных знаний

Вопрос к классу

1. Как называется числа а, b и с в записи a : b = c?

2. Как проверить правильность равенства а : b = с?

3. Как найти неизвестный множитель?

4. Как найти неизвестное делимое?

5. Как найти неизвестный делитель?

6. Как узнать, во сколько раз число а больше числа b?

7. Чему равна частное: а : 1; а : а; 0 : а?

8. Вычисли: 0,3 · 4; 0,5 · 5; 0,5 · 2.

9. Найди среди чисел пары равных: 3,1; 3,01; 3,10; 1,05; 1,5; 10,5; 1,050.

II. Формирование знаний

Учитель предлагает учащимся решить задачу.

1. Как найти неизвестный множитель в уравнении 4х = 1,2 ? Является корнем этого уравнения число 0,3? 3,30?

(Неизвестный множитель равен частному от деления произведения на известный множитель: х = 1,2 : 4, понятно, что х = 0,3, потому что 4 · 0,3 = 1,2.)

2. Как найти неизвестный делитель в уравнении 2,5 : х = 5? Является корнем этого уравнения число 5; 0,5; 0,05?

(Неизвестный делитель равен частному от деления делимого на частное:

х= 2,5:5, понятно, что корень х = 0,5, ибо 0,5 · 5 = 2,5).

Ученики вместе с учителем приходят к выводу:

1,2 : 4 = 0,3; 2,5 : 5 = 0,5.

После чего переходят к разбору первого примера в учебнике (от деления десятичной дроби на натуральное число «уголком» имеем:

4352 : 17 = 256, 43,52 : 17 = 2,56, потому

Следовательно, можно сказать, что при делении десятичной дроби на натуральное число (уголком) можно:

1) делить дробь на натуральное число, не обращая внимания на запятую;

2) после окончания деления целой части делимого надо в частном поставить запятую.

После этого ученики разбирают и записывают в тетрадях решение нескольких примеров на деление по составленной выше схеме.

После усвоения общего правила рассматриваются особые случаи (целая часть делимого меньше от делителя или равна 0; цифры делимого закончились, а 0 в остатка не получено; натуральное число делится на натуральное).

Вывод. В любом случае деления десятичной дроби на натуральное число выполняется почти так, как деление натуральных чисел. Отличие лишь в том, что в частном надо на определенном месте поставить запятую и можно дописать нули справа в дробной части.

III. Закрепления знаний. Формирование умений

Для лучшего усвоение алгоритма деления десятичной дроби на натуральное число на уроке решают лишь упражнения начального и среднего уровня сложности и каждый случай деления комментируется. На этом же уроке можно предложить учащимся решить примеры на совместные арифметические действия с десятичными дробями и уравнения, решение которых предусматривает деление десятичной дроби на натуральное число. Решение упражнений №№ 963; 965 (нечетные); 966(1,5,9); 968(1); 971(1,4).

IV. Итог урока

В конце урока учитель вместе с учащимися повторяет алгоритм выполнения деления десятичной дроби на натуральное число и акцентирует внимание учащихся на том факте, что это действие, так же, как и сложение, вычитание и умножение десятичных дробей сводится, фактически, в одноименных действий, но с натуральными числами.

V. Домашнее задание

п. 35, №№ 964; 967 (1-3); 970(1), 972(1,4).