
Деление рациональных чисел

Актуализация знаний
- Давайте вспомним определение модуля числа.
- Найти модули следующих чисел: |-5|=5, |37|=37, -|-13|=-13
- Вывод: модуль неотрицательного числа равен этому числу; модуль отрицательного числа равен числу, противоположному данному

Актуализация знаний
- Решите примеры: 14:2=, (-14):2=, 14:(-7)=, (-14):(-7)=
- Воспользуемся правилом: Частным двух чисел a и b называют такое число x, произведение которого с числом b равно числу a.
- То есть: a:b=x, справедливо, если справедливо равенство xb=a.

Тогда:
1. 7×2=14 14:2=7
x×b=a ⇒ a:b=x
2. (-7) ×2=-14 (-14):2=-7
x×b=a ⇒ a:b=x
3. 7×(-2)=-14 (-14):(-2)=7
x×b=a ⇒ a:b=x
4. -7 ×(-2)=14 14:(-2)=-7
x×b=a ⇒ a:b=x

Мотивация
Вы уже умеете складывать, вычитать, умножать и делить натуральные числа. А на этом уроке мы научимся делению рациональных чисел.

Наведение на факт
- Решите примеры: -20:5=? -20:(-5)=?

Для того, чтобы решить данные примеры, нам нужно понять, как делить числа с разными знаками. Для этого обратимся к решению прошлой задачи.

- Рассмотрим решение примера:
(-14):2=-7
2. Как при делении мы получили ответ (-7)?

1. Нужно найти модули чисел (-14) и 2
|-14|=14 |2|=2
2. Разделить модуль делимого на модуль делителя
14:2=7
3. Перед полученным числом поставить знак «-»
-7
4. Записать ответ
(-14):2=-7

Тогда при делении -20:5 получим:
1. Находим модули двух чисел
|-20|=20 |5|=5
2. Делим модуль делимого на модуль делителя
20:5=4
3. Перед полученным результатом ставим знак «-»
-4
4. Записываем ответ
-20:5=-4

Для проверки полученного результата воспользуемся уже известным нам правилом: a:b=x, справедливо, если справедливо равенство x × b=a.
Получим: -20:5=-4 ⇒ (-4)×5=-20
Решение верно

- Рассмотрим решение примера:
(-14):(-2)=7
2. Как при делении мы получили ответ 7?

1. Нужно найти модули чисел (-14) и (-2)
|-14|=14 |-2|=2
2. Разделить модуль делимого на модуль делителя
14:2=7
3. Записать ответ
(-14):(-2)=7

Тогда при делении -20:(-5) получим:
1. Находим модули двух чисел
|-20|=20 |-5|=5
2. Делим модуль делимого на модуль делителя
20:5=4
3. Записываем ответ
-20:(-5)=4

Для проверки полученного результата воспользуемся уже известным нам правилом: a:b=x, справедливо, если справедливо равенство x × b=a.
Получим: -20:(-5)=4 ⇒ 4×(-5)=-20
Решение верно

Формулировка правила
Можно сделать вывод, что при делении двух положительных чисел ответ – положительное число; при делении двух чисел с разными знаками ответ – отрицательное число; при делении двух отрицательных чисел ответ – положительное число.
+:+=+ +:- = - - :+= - - :- =+

Введение правила
Чтобы найти частное двух чисел с разными знаками, надо разделить модуль делимого на модуль делителя и перед полученным числом поставить знак «-».

Введение правила
Чтобы найти частное двух отрицательных чисел, надо разделить модуль делимого на модуль делителя.

Чтобы разделить два числа с разными знаками (-20) и 5, надо:
|-20|=20
2. Найти модуль делителя
|5|=5
3. Разделить модуль делимого на модуль делителя
20:5=4
4. Перед полученным числом поставить знак «-»
-4
5. Записать полученный результат
-20:5=-4

Чтобы найти частное двух отрицательных чисел (-20) и (-5) надо:
1. Найти модуль делимого
|-20|=20
2. Найти модуль делителя
|-5|=5
3. Разделить модуль делимого на модуль делителя
20:5=4
4. Записать полученный результат
-20:(-5)=4

Закрепление правила
Сформулируем алгоритм нахождения частного двух чисел с разными знаками:
1. Чтобы разделить два числа с разными знаками, необходимо:
2. Найти модуль первого числа, то есть модуль делимого;
3. Найти модуль второго числа, то есть модуль делителя;
4. Разделить полученные модули делимого на модуль делителя;
5. Перед полученным числом поставить знак «-»;
6. Записать результаты.

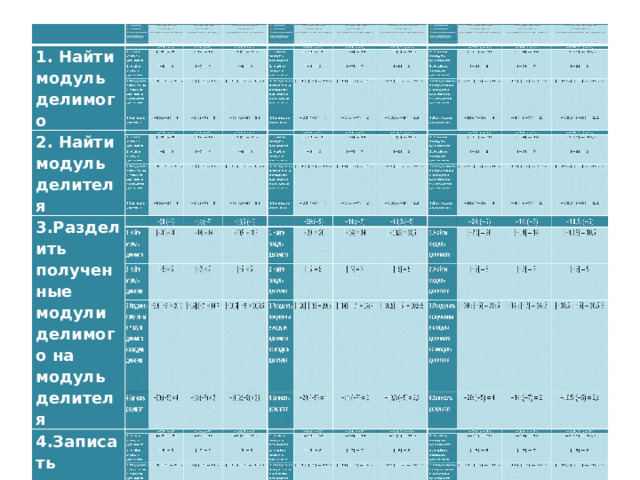
1. Найти модуль делимого
1. Найти модуль делимого
2. Найти модуль делителя
2. Найти модуль делителя
3.Разделить полученные модули делимого на модуль делителя
3.Разделить полученные модули делимого на модуль делителя
4. Перед полученным числом поставить знак «-»
4. Перед полученным числом поставить знак «-»
5.Записать результат
5.Записать результат

Закрепление правила
Сформулируем алгоритм нахождения частного двух отрицательных чисел:
1. Чтобы разделить два отрицательных числа, необходимо:
2. Найти модуль первого числа, то есть модуль делимого;
3. Найти модуль второго числа, то есть модуль делителя;
4. Разделить модуль делимого на модуль делителя;
5. Записать полученный результат.
1. Найти модуль делимого
1. Найти модуль делимого
2. Найти модуль делителя
2. Найти модуль делителя
3.Разделить полученные модули делимого на модуль делителя
3.Разделить полученные модули делимого на модуль делителя
4.Записать результат
4.Записать результат

1. У нас есть две ситуации деления рациональных чисел:
1.1 Деление двух чисел с разными знаками;
1.2 Деление двух отрицательных чисел;
2. Чтобы разделить два числа с разными знаками, надо:
1) Разделить модуль делимого на модуль делителя
2) Перед полученным числом поставить знак «-»
3. Чтобы разделить два отрицательных числа, надо:
1) разделить модуль делимого на модуль делителя




















































