Дидактическая игра на уроках математики как средство активизации познавательной деятельности обучающихся

Дидактические игры на уроках математики как средство активизации познавательной деятельности обучающихся

Содержание

№ п/п		Стр.
1.	Введение --------------------------------------------------------	3
2.	Основная часть
2.1.	Актуальность применения игры на уроке	4
2.2.	Дидактическая игра как средство активизации познавательной деятельности обучающихся	5
3.	Заключение -------------------------------------------------	11
4.	Литература --------------------------------------------------	12
5.	Приложения
5.1.	Математическое домино по теме «Формулы сокращенного умножения»	13
5.2.	Игра «Светофор»	14
5.3.	Игра «Фишка»	15
5.4.	«Соревнование художников»	16
5.5.	«Соревнование художников»	17
5.6.	Геометрия. О теореме Пифагора	18
5.7.	Примеры заданий для устной работы	19
5.8.	Все о бобрах	20
5.9.	Примеры кодированных упражнений	22
5.10.	Игра «Следствие ведут знатоки»	23
5.11.	Игра «Рейс на каждый день, кроме воскресенья»	24
5.12.	Игра «Туристический маршрут»	25
«Без игры не может быть полноценного умственного развития. Игра - это огромное светлое окно, через которое в духовный мир ребенка вливается живительный поток представлений, понятий. Игра - это искра, зажигающая огонек пытливости и любознательности» В.А. Сухомлинский

Введение.

Одной из актуальных проблем преподавания математики является повышение интереса школьника к изучаемому предмету. Математика относится к наиболее трудным предметам в школе, многие обучающиеся её не понимают, а, значит, с нежеланием идут на уроки. В связи с этим особое значение приобретает вопрос об уроках, где все дети чувствуют себя уютно, свободно и в то же время с азартом включены в работу, то есть сделан шаг к эффективности урока и преподавания в целом.

Усвоение – процесс познавательной деятельности, включающий ряд психологических процессов: восприятие, память, мышление. Оно непосредственно связано со свойствами личности, её чувствами, эмоциями, волевыми качествами. Поэтому задача учителя состоит в том, чтобы включить каждого ученика в учебно-познавательную деятельность, чтобы ученик получал радость и удовольствие от познания, переживал ситуацию успешности в учебном процессе. Учение с увлечением возможно лишь при одном условии: процесс познания должен быть творческим. Школьникам нужны тайна и стремление её раскрыть самостоятельно. Вот это и должен организовать учитель, причём на любом учебном материале.

Для осмысления, применения знаний, и чтобы математика не была «скучной», «сухой», непреодолимой, нужно использовать активные методы обучения. Одним из путей решения этой проблемы является организация игровой деятельности на уроках. В процессе игры замечательный мир детства соединяется с прекрасным миром науки, в который вступают обучающиеся. Цель данной работы состоит в раскрытии педагогического смысла игры, рассмотрении различных типов нестандартных уроков как один из методов активизации познавательной деятельности обучающихся на уроках математики.

2.1. Актуальность применения игры на уроке.

Особое внимание на уроках уделяем дидактическим играм, что помогает не только проверять и углублять знания обучащихся, развивать их способности, но и успешно вести коррекционно – развивающую работу с учащимися. Все чаще в настоящее время встречаются школьники (разного возраста), для которых характерны повышенная утомляемость, сниженная работоспособность, неумение выделить главное, установить причинно – следственные связи. Значительно более низкими оказываются как точность, так и скорость интеллектуальных действий. Как следствие – низкая произвольность деятельности, неумение сосредоточиться на решаемой задаче, подчинить ей свои действия, выбрать адекватные средства для достижения цели.

Все это не только затрудняет учебный процесс, но и снижает интерес школьника к предмету. А значит и результаты усвоения материала, качество знаний также по предмету снижаются.

Повышение активности ребенка в процессе обучения остается одной из важнейших задач любого учителя. Активность такого рода может быть вызвана при помощи целенаправленных педагогических воздействий. Один из способов такого воздействия является проведение нестандартных уроков, уроков необычных по замыслу и организации. Такие уроки гораздо больше нравятся школьникам, чем обычные будничные занятия.

Применение игровых технологий на уроке – эта тема была актуальна всегда не только для учителей математики. 
Актуальность применения игровых технологий на уроках математики мы видим в том, что: 
- игровые формы обучения на уроках создают возможности эффективной организации взаимодействия учителя и учащихся, продуктивной формы их общения с присущими им элементами соревнования, непосредственности, неподдельного интереса; 
- в игре заложены огромные воспитательные и образовательные возможности; 
- в процессе игр дети приобретают самые различные знания о предметах и явлениях окружающего мира; 
- игра развивает детскую наблюдательность и способность определять свойства предметов, выявлять их существенные признаки; 
- игры очень хорошо уживаются с “серьезным” учением; 
- включение в урок игр и игровых моментов делает процесс обучения интересным и занимательным, создает у детей бодрое рабочее настроение, облегчает преодоление трудностей в усвоении учебного материала; 
- разнообразные игровые действия, при помощи которых решается та или иная умственная задача, поддерживают и усиливают интерес детей к учебному предмету. 
- игры оказывают большое влияние на умственное развитие детей, развивая и совершенствуя их мышление, внимание, творческое воображение. 

2.2. Дидактическая игра как средство активизации познавательной деятельности обучающихся.

В решении этих задач большую помощь оказывают применяемые на уроках дидактические игры. Слово «дидактика» происходит от греческого «дидактикос», что означает «обучающий». А дидактика - это область педагогики, исследующая закономерности процесса обучения. Особенностью дидактической игры в отличии от игр вообще является существенный признак – наличие чётко поставленной цели обучения и соответствующего ей педагогического результата.

Дидактическая игра имеет устойчивую структуру, включающую следующие основные компоненты: игровой замысел, правила, игровые действия, познавательное содержание или дидактические задачи, оборудование, результат игры. Игровой замысел выражен, как правило, в названии игры, он заложен в той дидактической задаче, которую надо решать на уроке. Придаёт игре познавательный характер, предъявляет к её участникам определённые требования в отношении знаний. Правилами определяется порядок действий и поведения обучающихся в процессе игры, создаётся рабочая обстановка на уроке. Поэтому их разработка ведётся с учётом цели урока и возможностей обучающихся.

В процессе игры у детей вырабатываются привычки сосредотачиваться, мыслить самостоятельно, развивается внимание, стремление к знаниям. Увлёкшись, дети не замечают, как учатся: познают, запоминают новое, ориентируются в необычных ситуациях, пополняют запас представлений, понятий, развивают фантазию. Даже самые пассивные из детей включаются в игру с огромным желанием, прилагая все усилия, чтобы не подвести товарищей по игре. Таким образом, игра является мощным средством побуждения и стимулирования обучающихся к математической деятельности.

Основой дидактической игры, которая пронизывает собой её структурные элементы, является познавательное содержание. Оно заключается в усвоении знаний и умений, применяемых при решении учебной проблемы, поставленной игрой.

Кроме того, игры развивают ум и творческие способности детей, потому что учат их выбирать из разных вариантов наилучший. Игры формируют волю, активность, самостоятельность, обогащают чувства, дают возможность испытать радость от сознания собственных сил, помогают социальной адаптации, корректируют самооценку.

Практически любую проблему можно решить с помощью игры, если внести элемент соревнования или предложить участникам войти в какую – либо роль. Если сложный теоретический вопрос решается путём дискуссии сторонников разных точек зрения, и ребята выступают в качестве исследователей, если стоит вопрос «кто быстрее, лучше, интереснее выполнит задание?», - это уже игра, которая зачастую оказывается наиболее продуктивной формой работы с детьми.

На своих занятиях используем разные виды игр, выбор которых продиктован целями урока.

Это, прежде всего игры обучающие, контролирующие, обобщающие.

Обучающей будет игра, если учащиеся, участвуя в ней, приобретают новые знания, умения и навыки или вынуждены приобретать их в процессе подготовки к игре. Причём результат усвоения знаний будет тем лучше, чем чётче будет выражен мотив познавательной деятельности не только в игре, но и в самом содержании математического материала.

Контролирующей будет игра, дидактическая цель которой состоит в повторении, закреплении, проверке ранее полученных знаний. Для участия в ней каждому обучающемуся необходима определённая математическая подготовка.

Обобщающие игры требуют интеграции знаний, они способствуют установлению меж предметных связей, направлены на приобретение умений действовать в различных учебных ситуациях.

В курсе математики много различных формул. Чтобы обучающиеся могли свободно оперировать ими при решении задач и упражнений, они должны самые распространённые из них, часто встречающиеся на практике знать наизусть. Чтобы формулы лучше запоминались, а также для контроля за их усвоением можно использовать игру «Математическое домино», состоящую из 12-30 карточек. Каждая карточка разделена чертой на две части: на одной записано задание, на другой - ответ к другому заданию. Чтобы убедится в правильности выполнения, с обратной стороны карточек можно написать какое-нибудь изречение или нарисовать часть картинки, домино переворачивается и выкладывается изречение или картинка целиком. (Приложение 1).

Сигнальные карточки (красная, зелёная) очень помогают дисциплинировать обучающихся и одновременно дают информацию об усвоении материала. Например, при устном опросе можно провести игру «Светофор». Если обучающийся согласен с ответом, то он поднимает зелёную карточку, а если нет - красную. Таким образом, каждый имеет возможность высказаться. (Приложение 2).

Для устного счёта можно использовать игру «Лучший счётчик». Обучающимся предлагается дома подобрать несколько примеров для устного счёта по данной теме. Класс делится на команды. В каждой команде выбирается «счётчик», который будет защищать честь своего коллектива. Примеры для устного счёта предлагают «счётчику» члены других команд до тех пор, пока он не собьётся. Затем его сменяет другой обучающийся из той же команды, и игра продолжается. Число «счётчиков» для одного тура определяется по договорённости. Побеждает команда, в которой было наименьшее число «счётчиков», решивших наибольшее количество примеров. Среди «счётчиков» устанавливается также личное первенство.

Для обработки навыков сложения и вычитания целых чисел, а также их сравнения можно использовать игру «Фишка». Первоначально фишка стоит на любой линии старта. Обучающийся двигает фишку по таблице с числами. За один ход по правилам игры он может продвинуть её на ближайшее соседнее поле по вертикали или диагонали. При переходе из одной клетки в другую надо прибавить число, записанное в клетке, на которую поставили фишку. Выигрывает тот, кто на линии финиша получит наибольшее число. (Пример таблицы Приложение 3.)

Примером обучающей игры может служить игра «Соревнование художников», при изучении темы «Координатная плоскость». На карточках записаны координаты точек. Если на координатной плоскости каждую точку последовательно соединить с предыдущей, то в результате получится определённый рисунок. В этом заключается игровой замысел. Дидактическая задача – научить строить точки по данным координатам, а результат игры- усвоение темы, хорошая оценка и большое удовольствие. Игра носит практический характер. Но обучающиеся выполняют и обратное задание: приносят рисунки, имеющие конфигурацию ломаной, с записью координат точек, по которым они могут быть построены. Строить рисунок по координатам можно и при изучении других тем. Например, при изучении темы «Квадратные уравнения», «Системы уравнений» можно предложить решить уравнения (системы уравнений) и полученные результаты нанести на координатную плоскость, в результате должен получиться рисунок, соответствующий названию. (Приложения 4, 5).

Математика имеет множество великолепных приложений к различным, самым неожиданным аспектам человеческой деятельности, а в школьном учебнике лишь вскользь упоминается о некоторых из этих приложений. В результате, по словам профессора Александра Яковлевича Хинчина, в сознании обучающихся со стихийной неизбежностью возникает представление о «сухости», формальном характере математики, оторванности её от жизни и практики. Так кто же, если не учитель математики, должен навести мосты, соединяющие математику с окружающим миром? Полагаем, что учитель математики должен на своих уроках показать взаимосвязь естественно-математического цикла с гуманитарным, наполнив уроки конкретными фактами, яркими образами и сделав их содержательнее, разнообразнее, занимательнее.

Одним из наиболее эффективных направлений гуманитаризации обучения математики является использование поэзии на уроках. Например, стихотворение Евгения Винокурова посвящено геометрии, практически это гимн геометрии и одновременно посвящение одному из чудесных городов России - Санкт-Петербургу. Его можно использовать на вводных или обобщающих уроках геометрии. (Приложение 6).

Теорема Пифагора является одной из самых знаменитых в истории математики. Ею пользовались школьники Древнего Вавилона во втором тысячелетии до нашей эры, она была в частных случаях известна в древнеиндийской математике. При изучении темы «Теорема Пифагора» можно использовать стихотворение А. Фон Шамисо «О теореме Пифагора». (Приложение 6).

Большой популярностью пользуются на уроках математики задачи в стихах. При изучении темы «Квадратные уравнения» можно предложить обучающимся решить задачу Бхаскары:

«Обезьянок резвых стая,

Всласть поевши, развлекалась.

Их в квадрате часть восьмая

На полянке забавлялась.

А двенадцать по лианам

Стали прыгать, повисая.

Сколько ж было обезьянок,

Ты скажи мне, в этой стае?»

При изучении темы «Десятичные дроби» - задачу про медведя:

Медведь с базара плюшки нёс,

Но на лесной опушке

Он половину плюшек съел

И плюс ещё полплюшки.

Шёл, шёл, уселся отдохнуть

И под «ку-ку» кукушки

Вновь половину плюшек съел

И плюс ещё полплюшки.

Стемнело, он ускорил шаг,

Но на крыльце избушки

Он снова пол-остатка съел

И плюс ещё полплюшки.

С пустой кошёлкою – увы!

Он в дом вошёл уныло…

Хочу, чтоб мне сказали вы

А сколько плюшек было?

У А. С. Пушкина в «Скупом рыцаре» рассказана старинная легенда восточных народов:

«Читал я где-то,

Что царь однажды воинам своим

Велел снести земли по горсти в кучу, -

И гордый холм возвысился,

И царь мог с высоты с весельем озирать

И дол, покрытый белыми шатрами,

И море, где бежали корабли.»

При изучении темы «Объём конуса» обучающимся можно задать вопрос: «Какой высоты мог быть такой холм? Действительно ли открывалась с его высоты такая панорама?»

Практика преподавания показывает, что устные задания по математике – это одно из сильнейших средств повышения качества знаний обучающихся. Устную работу можно проводить в занимательной форме. (Примеры заданий для устной работы в Приложении 7.)

Упражнения с использованием нематематической информации, разнообразные формы подачи условий (таблицы, схемы, программы, магические квадраты, блок-схемы, лабиринты, удивительные квадраты) наиболее подходят для повторения и обобщения пройденного материала. Приведем пример задания «В мире животных», которое можно назвать «Всё о бобрах» (Приложение 8). В рассказ о бобрах включены задания, выполнение которых предусматривает вычислительную работу, форма подачи заданий разнообразна. Упражнение на определение длины тела бобра направлено на логическое развитие мышления, понимание смысла частицы «не». Упражнение на определение времени преследует цель обучения грамотному правописанию математических терминов, что является одной из обязательных задач учителя. В процессе выполнения задания осуществляется смена деятельности, что способствует предупреждению или снятию утомления. Использование на уроке математики нематематической информации направлено на воспитание у обучающихся любознательности, стремления познавать новое, расширение кругозора.

Кодированные упражнения можно использовать при изучении практически всех тем. Например, узнайте имя сказочной героини, решив примеры на сложение и вычитание натуральных чисел. Ответ соответствует определённой букве.

1.

2.

3.

4.

5.

6.

7.

1. (3+12)+3-18

2. 46+87+13+14

3. (138+39)-36

4. 89645+129-89714

5. 20220-(25860-5740)

6. 678+(324-187)-800

7. 75000-54207+7-20795

л	к	з	м	о	ш	и	н	у	а
141	15	0	10	160	100	140	105	60	5

Решив примеры, обучающиеся получают имя (Золушка).

Примеры кодированных упражнений по темам «Формулы сокращённого умножения» и «Решение неравенств с одной переменной» (Приложение 9).

Для проверки знаний обучающихся по теме можно использовать игру «Следствие ведут знатоки». В начале урока зачитывается шутливое письмо, в котором профессор Цифиркин просит разыскать похищенную неизвестными ценную математическую фигуру. Следователи (класс делится на две команды) должны пройти конкурс на лучшую подготовку к следствию. Задания конкурсов- задачи по заданной теме. По итогам этих конкурсов выбирается лучшая команда, которая получает «след», на котором написано условие задачи. Решив её, команда находит пропавшую фигуру. (Приложение 10.)

Самостоятельное выполнение задания - самый надёжный показатель качества знаний, умений и навыков обучающегося. Вместо обычной самостоятельной работы можно провести игру с использованием картинок-заданий. Работа выполняется на листочках. Если рисунок яркий, то задание выполняется с большим интересом. Рисунок выдаётся перед началом работы каждому обучающемуся.

Игра «Рейс на каждый день, кроме воскресенья» по теме «Сложение и вычитание десятичных дробей».

Среди раздольных лугов, полей, лесов и болот затерялся бы посёлок Осиновск. Затерялся бы, может быть, если бы не было в нём современной, богатой животноводческой фермы. На ферме многочисленное стадо коров, а молоко с этой фермы славится во всей округе.

Каждое утро дядя Егор гордо садится за руль своей «Газели» и согласно заключённым договорам развозит молоко по окрестным деревням и дачным посёлкам. А там его уже ждут каждый день, кроме воскресенья. На каждый день – свой маршрут. По картинке можно проследить путь дяди Егора и ответить на предложенные вопросы. (Приложение 11.).

Маршрут.

Понедельник. Осиновск-Дубиха-Пичугино-Осиновск.

Вторник. Осиновск-Сосновка (через Дубиху) и обратно.

Среда. Осиновск-Ивкино- Дубиха- Пичугино-Осиновск.

Четверг. Осиновск-Ивкино и обратно.

Пятница. Осиновск-Ивкино-Малые Болота- Пичугино-Осиновск.

Суббота. Осиновск-Дубиха- Сосновка- Ивкино- Осиновск.

Вопросы:

1. Вычислить длину каждого маршрута.

2. На сколько больше надо проехать во вторник, чем в четверг?

3. На сколько больше надо проехать в среду, чем в субботу?

4. На сколько километров Дубиха ближе к сосновке, чем Кленики?

Игра «Туристический маршрут» по теме «Нахождение дроби от числа».

На рисунке (Приложение 12.) показан туристический маршрут длиной 40 км. Отмечено начало маршрута. На маршруте установлены рекламные щиты, на каждом надо сделать указатель достопримечательности, расположенной поблизости от него. Местность, по которой проходит маршрут, овеяна легендами. Всего надо установить 14 рекламных щитов.

Чтобы правильно разместить рекламу, надо посмотреть, на каком расстоянии от начала маршрута находится объект. Например, известно, что ресторан находится на расстоянии 7/20 от начала маршрута. Значит, найдя 7/20 от 40, т.е. получив 14, можно было бы поставить рекламный щит около указателя расстояния, равного 14 км. Такого щита пока нет. Но есть много других. На каждом из них надо нарисовать соответствующий символ, такой, какой показан на рисунке. Более подробное изображение не требуется.

Обучающиеся выполняют работу на листе с изображением маршрута, рисуя на каждом щите нужное изображение. Тем, кто раньше других справился с заданием, предлагается на обороте листа написать несколько легенд, связанных с достопримечательностями.

Заключение.

Подводя итог работы, можно сделать следующие выводы.

Чтобы математика не была «сухой» и малоинтересной наукой, надо прививать интерес к ней как на уроках, так и на внеурочных занятиях. А чтобы достичь этого, необходимо обогащать содержание материала по истории науки, решать задачи повышенной сложности и нестандартные задачи. Игровые формы занятий, нестандартные уроки - это всегда уроки-праздники, когда активны все обучающиеся. Каждый имеет возможность проявить себя, класс становится творческим коллективом. Нет такого школьного предмета, на котором применение различных игр было бы нецелесообразно. Нестандартные уроки используются как итоговые уроки при обобщении и закреплении знаний, умений и навыков. Как правило, они посвящены какой-то теме, и для её раскрытия уже нужно обладать определённым набором знаний. Нельзя сказать, что использование игровых ситуаций, нестандартных уроков даёт возможность обучающимся овладеть математикой «легко и счастливо». И слишком частое обращение к подобным формам организации учебного процесса нецелесообразно, так как приводит к потере устойчивого интереса к предмету, и нетрадиционное может быстро стать традиционным. Необходимо использовать все возможности, для того, чтобы дети учились с интересом, чтобы большинство из них испытали и осознали притягательные стороны математики, её возможности в совершенствовании умственных способностей, в преодолении трудностей.

Игровая деятельность - лучшее для этого средство. Именно она позволяет направлять познавательную деятельность обучающихся, развивать творческие способности личности. Возникает цель реального достижения, а урок приобретает черты состязательности, сотрудничества. Игра ценна своей мотивацией, особым творческим, партнёрским состоянием личности. Участие в ней обучающихся – самая свободная форма проявления их деятельности, в которой осознаётся окружающий мир, открывается широкий простор для проявления своего «я», активности, самовыражения. Благодаря нестандартным урокам, формы работы учителя станут ещё более разнообразными. Обучающиеся ждут от нас больше интересных уроков, на которых мы организуем эффективную творческую деятельность - при этом повышается интерес к предмету и качественная успеваемость.

Литература.

1. Левченко И.Ю., Приходько О.Г. «Технологии обучения и воспитания детей с нарушениями опорно-двигательного аппарата». Москва 2001г.

2. Коваленко В.Г. «Дидактические игры на уроках математики», Москва «Просвещение», 1990г.

3. Кузнецов Б.Н. «Воспитание интереса к изучению математики в школе». Иркутск , изд. Иркутского университета, 1989г.

4. Ерохина Е.В. «Игровые уроки математики». Изд. Грамотей, 2004г.

5. Аникеева Н.П. «Воспитание игрой». М. Просвещение, 1987г.

6. Ляпина Г.А. «Игра как средство активизации учебно – воспитательного процесса». Алма-Ата, Мектеп, 1978г.

7. Математика в школе, №1, 1993г.

8. Маркова А.К., Матис Т.А. «Формирование мотивации учения». Москва, 1990г.

9. Щукина Г.И. «Активизация познавательной деятельности учащихся в учебном процессе». М., Просвещение, 1979г.

10.Российская педагогическая энциклопедия. М. Научное издательство «Большая Российская энциклопедия», 1993г.

5.1. Приложение 1.

Математическое домино по теме

«Формулы сокращенного умножения».

(а-в)(а+в) 4+4а+а²

а²-в² а²+2ав+в²

(2+а)² 25-10а+а²

(а+в)² а²-10а+25

(5-а)² 16у²-16ух+4х²

4х²+4х+1 а²-100

(3а+2в)² 49-14а+а²

(2-в)(2+в) а²-2а+1

(4у-2х)² (у-3)(у+3)

16х²-40ах+25а² у²-9

1-4х+4х² (а-в)²

(а-5)² 9а²+12ав+4в²

(4х-5а)² а²-2ав+в²

(2х+1)² (1-2х)²

(а-10)(а+10) 4-в²

(а-1)² (7-а)²

5.2. Приложение 2.

Игра «Светофор» (на примере темы «Делимость чисел»).

Если обучающийся согласен с утверждением, то он поднимает зелёную карточку, если нет - красную.

1. Любое число, делящееся на 10, делится и на 5;

2. Любое число, делящееся на 3, делится и на 9;

3. Любое число, делящееся на 10, делится на 2;

4. Любое число, делящееся на 2, делится и на 10;

5. Все чётные числа являются составными;

6. Любое число можно разложить на простые множители;

7. Простых чисел бесконечно много.

8. Шестиклассники решали задачу: «Таня купила в магазине яйца и положила их в небольшую корзиночку. По дороге домой она сообразила, что число яиц делится и на 2, и на 3, и на 5, и на 10, и на 15. Сколько яиц купила Таня?». Витя Верхоглядкин поднял руку самый первый. Когда его спросили, он с гордым видом ответил: - «Эта задача решения не имеет. Чтобы найти число яиц, надо перемножить 2, 3, 5, 10, 15. получится 4500 яиц. Разве может в одной корзинке поместится столько яиц?»

Кто согласен с решением Вити?

Кто скажет, в чём Витя ошибся?

5.3. Приложение 3.

Игра «Фишка»

финиш					старт
6	-7	35	-9	33	100
5	-8	38	-8	32	100
4	-9	40	-7	31	100
3	-10	52	-9	22	100
2	-7	35	-8	30	100
3	-8	50	-7	29	100
4	-9	37	-9	28	100
5	-10	39	-6	24	100
6	-7	42	-5	26	100
7	-8	50	-4	25	100
8	-9	45	-6	24	100
9	10	47	-7	23	100

5.4. Приложение 4.

«Соревнование художников»

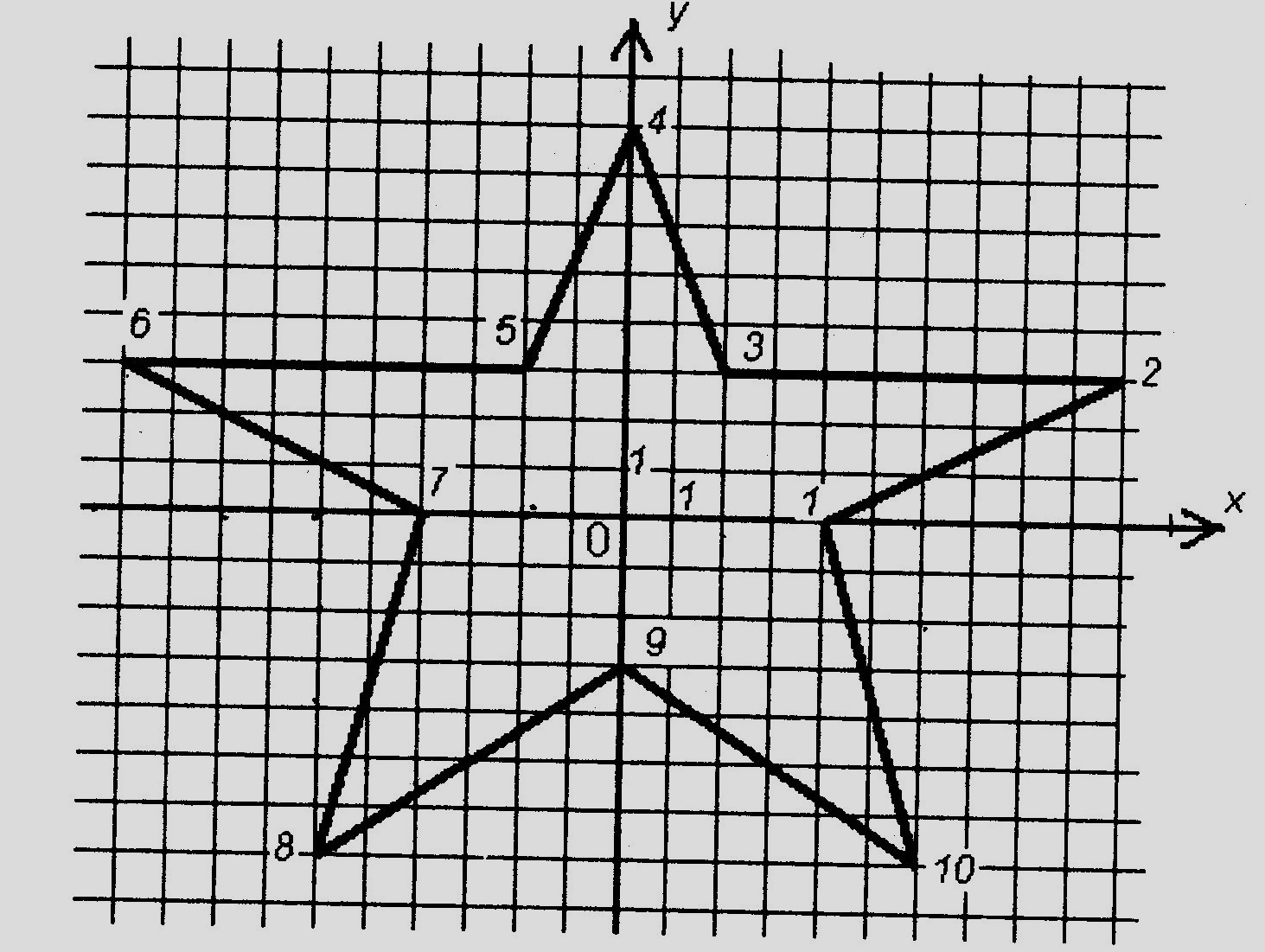
Нарисуйте портрет инопланетянина по заданным координатам.

(3;14), (4;15), (3;16), (2;15), (3;14), (0;7), (1;6), (-2;3), (-4;3), (-2;2),

(-1;1), (0;2), (1;1), (2;2), (3;2), (4;2), (5;1), (6;2), (3;5), (0;2), (0;0),

(1;-1), (1;-3), (2;-4), (2;-7), (0;-7), (0;-8), (1;-9), (3;-7), (5;-9), (6;-8),

(6;-7), (4;-7), (4;-4), (5;-3), (5;-1), (6;0), (6;2), (7;1), (8;2), (10;3),

(8;3), (5;6), (6;7), (3;14).

Глаза: (1;8), (2;9), (3;8), (4;9), (5;8).

Рот: (1;7), (2;6), (4;6), (5;7), (1;7).

Запишите координаты вершин звёздочки.

5.5. Приложение 5.

«Соревнование художников»

Решите квадратные уравнения, меньшее значение корня обозначить х₁, большее обозначить х₂ (х₂x₁;x₁x₂). В скобках после каждого уравнения указан «код»: (х₁; х₂) или (х₂; х₁) – координаты точек координатной плоскости. После того, как все уравнения будут решены, в соответствии с полученными результатами нанести на координатной плоскости точки и последовательно их соединить, последнюю точку замкнуть с первой точкой.

Должен получиться рисунок, соответствующий названию.

Катер. Ваза.

1. х²-16х=0, (х₂;х₁). 1) х²-4х-21=0, (х₁;х₂).

2. х²-14х-15=0, (х₁;х₂). 2) х²-10х+21=0, (х₁;х₂).

3. х²+х=0, (х₁;х₂). 3) х²-7х+12=0, (х₁;х₂).

4. х²+3х=0, (х₁;х₂). 4) х²-6х=0, (х₂;х₁).

5. х²+7х-98=0, (х₁;х₂). 5) х²+4х-32=0, (х₂;х₁).

6. х²+14х=0, (х₁;х₂). 6) х²+6х-55=0, (х₂;х₁).

7. х²+15х=0, (х₁;х₂). 7) х²+16х+55=0, (х₂;х₁).

8. х²+15х+56=0, (х₁;х₂). 8) х²+12х+32=0, (х₂;х₁).

9. х²-х-56=0, (х₂;х₁). 9) х²+6х=0, (х₁;х₂).

10)-5х²+80х=0, (х₂;х₁). 10) х²-х-12=0, (х₁;х₂).

5.6. Приложение 6.

Геометрия.

О Петр, ведь ты построил город

Не для умерших – для живых?..

Тяжёлый дождь бежит за ворот

Окаменевших часовых.

Недвижимы аллеи парков,

Прямы проспекты как стрела.

Сильней божественных монархов

Здесь геометрия была.

Был нежен в башнях цитадели

И кроток лепет голубиц…

И, странные, на мир глядели

В окно глаза цареубийц.

Гуляют каменные финны,

Курятся трубки из бород.

Вот и построили Афины

Среди топей северных болот!

Налево львы. И львы направо.

А у заставы инвалид

Штык держит вертикально прямо,

Как геометрия велит.

О теореме Пифагора.

Уделом истины не может быть забвенье,

Как только мир её увидит взор;

И теорема та, что дал нам Пифагор,

Верна теперь, как в день её рождения.

За светлый луч с небес вознёс благодарение,

Мудрец богам не так, как было до тех пор,

Ведь целых сто быков послал он под топор,

Чтоб их сожгли, как жертвоприношение.

Быки с тех пор, как только весть услышат,

Что новой истины уже следы видны.

Отчаянно мычат и ужаса полны:

Им Пифагор навек внушил тревогу.

Не в силах преградить той истины дорогу

Они, закрыв глаза, дрожат и еле дышат.

5.7. Приложение 7.

Примеры заданий для устной работы:

1. Был он долго неизвестным, но по сказке интересной стал он каждому знаком. Он весёлый, добрый, смелый, он отважный и умелый. В царстве овощей живёт. Вы примеры все решите, как, зовут его, скажите. Поменяйте местами карточки, на которых записаны примеры с одинаковыми ответами, и вы узнаете имя смелого и доброго мальчика.

166 л

89 и

213 н

127 о

214 о

97 п

612 и

812 ч

195 л

2.

35

54

45

40

42

48

36

56

28

32

49

	4	5	6	7
6	ю	т	и	а
7	д	н	а	ы
8	н	ь	р	а
9	и	т	и	ь

Числами зашифровано известное выражение. Догадайтесь, как по таблице найти буквы, соответствующие числам. Запишите эти буквы и прочитайте полученные слова.

Объясните: как вы понимаете крылатое выражение «Нить Ариадны»?

(Это слова из мифа об афинском герое Тезее. Ариадна, дочь Критского царя Миноса, помогла Тезею в сражении с чудовищем Минотавром. Минотавр, по мифу, получеловек-полубык. Ариадна дала Тезею клубок ниток, с помощью которых Тезей после победы над Минотавром сумел благополучно выбраться из лабиринта- жилища Минотавра.)

5.8. Приложение 8.

«Всё о бобрах».

В нашей стране водится много бобров. Бобр - крупный грызун, ведёт полуводный образ жизни, обитает по лесным рекам, сооружает из ветвей и ила домики, поперёк реки делает плотины длиной 5-6 метров.

Задание 1. Узнайте длину тела бобра (в дециметрах). Поможет вам удивительный квадрат.

5,9	6,3	3,6
2,3	2,7	0
3,7	4,1	1,4

1. Из первой строки выберите наименьшее число.

2. Из второй строки выберите наибольшее число.

3. Из третьей строки выберите не наименьшее и не наибольшее число.

4. Найдите сумму выбранных трёх чисел – и вы получите ответ на вопрос.

(3,6+2,7+3,7=10, длина тела бобра 10дм.)

10 дм – сколько это сантиметров? Сравните длину тела бобра со своим ростом.

Задание 2. Узнайте массу бобра (в килограммах)

 кг 8207= -1500= +61=

Как называются геометрические фигуры, используемые в этом задании?

Используя результаты вычислений, ответьте на вопросы:

- На сколько 100 больше 39?

- Во сколько раз 25 меньше 100?

- На сколько надо умножить39, чтобы получить 156?

- Чему равно частное от деления 1656 на 8?

Очень ценятся мех и кожа бобра. Из жира бобра изготовляют лекарство. Бобр отличный пловец и ныряльщик, несколько минут он может находиться под водой.

Задание 3. В строки таблицы впишите названия чисел:

900, 600, 1000, 500. В одном из столбцов прочтите название числа, указывающего, сколько минут бобр может находиться под водой.

5 минут – сколько это секунд?

Какую часть 5 минут составляют от 1 часа?

5.9. Приложение 9.

Примеры кодированных упражнений

Задание 1.

Помоги человечку решить неравенство. Соедини равносильные неравенства стрелочками.

3(3х-1)2(5x-7)

9x-310x-14 9x+310x-14 9x-3x-14

9x-10xx-10x3-14 9x-10x-3-14

-x-17 -xx-11

xx11 x17

ответ: x11 , x17 , x

Задание 2.

Расшифруй слово, упростив выражение.

Соедини равносильные выражения стрелочками и узнаешь зашифрованное слово.

С: (у+3)²-(у-2)(у+2)

А: у²+3у+9-у²+4 О: у²+6у+9-у²+4 У: у²-6у+9-у²-4

К: 6у+13 П: 3у+13 Д: -6у+5

Ответ: сок, сад, суп.

5.10. Приложение 10.

Игра «Следствие ведут знатоки» (по теме «Квадратные уравнения»).

Ученикам 9 класса школы №___ от профессора Цифиркина Заявление 25.09. сего года у меня из кабинета исчезла ценная математическая фигура. Прошу принять меры для розыска этой фигуры. С уважением профессор Цифиркин. P.S. Преступник оставил «след», который я прошу передать той из команд, которая лучше подготовится к розыску.

Конкурс на лучшую подготовку к следствию.

Задания командам.

1. Проверка быстроты реакции:

а) х²-81+0; а) х²-8х=0;

б) 16х²=49. б) 5х²=12.

2. Умение вести перекрестный допрос:

Один ученик из каждой команды выбирается в качестве свидетеля. Команда противников задаёт ему вопрос по теме «Квадратные уравнения».

3. Проверка логического мышления:

При каком с уравнение имеет единственный корень?

3х²-2х+с=0?  х²+сх+9=0?

4. Умение проводить экспертизу:

Установить, являются ли числа 4+3 и 4-3 корнями уравнения

х²-8х+13=0,

способом подстановки.  с помощью теоремы Виета.

Победившая команда получает «след» с задачей.

Задача.

В уравнении х²+рх-140=0 один из корней равен –28. Число р укажет номер кабинета, а второй корень- стол, где находится указанная фигура.

5.11. Приложение 11.

Игра «Рейс на каждый день, кроме воскресенья»

5.12. Приложение 12.

Игра «Туристический маршрут»